使用ID3算法实现决策树

决策树

基本介绍：
决策树通过把数据样本分配到某个叶子结点来确定数据集中样本所属的分类。
决策树由决策结点，分支和叶子结点组成。

• 决策结点表示在样本的一个属性上进行的划分；

• 分支表示对于决策结点进行划分的输出；

• 叶子节点代表经过分支到达的类。

从决策树根据节点出发，自顶向下移动，在每个决策结点都会进行次划分，通过划分的结果将样本进行分类，导致不同的分支，最后到达个 叶子结点，这个过程就是利用决策树进行分类的过程。

ID3算法原理

ID3算法是在每个结点处选取能获得最高信息增益的分支属性进行分裂。

在每个决策结点处划分分支，选取分支属性的目的就是将整个决策树的样本纯度提高。

衡量样本集合纯的指标则是熵（熵越大，所含有用信息就越少，不确定性就越大，在决策树中，熵指的是纯度，熵越小，纯度越高），设S为数量为n的样本集，其分支属性有m个取值用来定义m个不同分类Ci（i=1，2，3，…，m）那么熵为：

计算分支属性对于样本集分类好坏程度的度量——信息增益。
由于分裂后样本集的纯度提高，则样本集的熵降低，熵降低的值即为该分裂方法的信息增益：

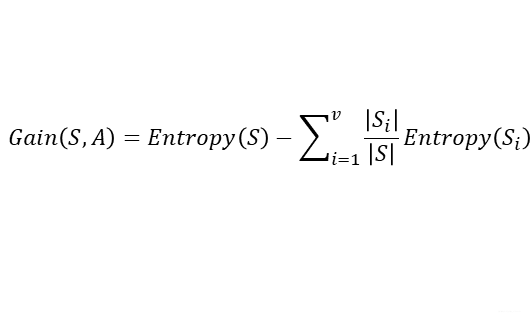
ID3代码

1. 第一步，创建数据和标签。

from math import log
import operator#用于函数操作

def create_data():  # 构建数据和标签
    dataSet = [['short', 'long hair', 'thin', 'female'],
               ['high', 'short hair', 'thin', 'male'],
               ['short', 'long hair', 'fat', 'female'],
               ['high', 'long hair', 'thin', 'female'],
               ['short', 'short hair', 'fat', 'male'],
               ['short', 'short hair', 'thin', 'female'],
               ['high', 'short hair', 'fat', 'male'],
               ['high', 'long hair', 'fat', 'male'],
               ['short', 'short hair', 'thin', 'male'],
               ['high', 'short hair', 'thin', 'female'],
               ['short', 'long hair', 'fat', 'female']]
    labels = ['stature', 'hair', 'weight', 'gender']
    return dataSet, labels

2. 使用ID3算法需计算信息熵，所以第二步创建cal_entropy方法来计算信息熵。

def cal_entropy(dataSet):
    num = len(dataSet)      #总共有多少行数据
    label_count = {}
    for fea in dataSet:     #遍历整个数据集，每次取一行
        current_label = fea[-1]  # 统计每条数据的类，取该行最后一列的值，即标签
        if current_label not in label_count.keys():     #判断在字典中标签是否存在
            label_count[current_label] = 0
        label_count[current_label] += 1  # 计算每个类中有多少数据
    entropy = 0.0           #初始化信息熵
    for i in label_count:  # 计算经验熵
        Pi = float(label_count[i]) / num
        entropy -= Pi * log(Pi, 2)
    return entropy      #返回信息熵

3. 第三步，创建remove_feature方法来去除某个特征，对数据集进行分割。

def remove_feature(dataSet, axis, feature):  # 去除某个特征
    retdataset = []
    for featVec in dataSet:
        if featVec[axis] == feature:
            reducedata = featVec[:axis]  # 某个特征前数据
            reducedata.extend(featVec[axis + 1:])  # 某个特征后数据
            # 去掉了axis
            retdataset.append(reducedata)
    return retdataset

4. 第四步，通过信息熵计算信息增益率来求出划分数据集的最优信息增益比。

def choose_best_feature(dataSet):
    entropy = cal_entropy(dataSet)
    feature_num = len(dataSet[0]) - 1      #获取当前数据集的特征个数，最后一列是分类标签
    max_mutual_info = 0
    best_feature = -1       #初始化最优特征
    for i in range(feature_num):
        feature_list = [example[i] for example in dataSet]  #获取数据集中当前特征下的所有值
        feature_class = set(feature_list)  # 得到该特征的所有可能取值
        conditional_entropy = 0
        for value in feature_class:
            retdataset = remove_feature(dataSet, i, value)  #去处某一特征，方便计算
            Pi = len(retdataset) / float(len(dataSet))
            conditional_entropy += Pi * cal_entropy(retdataset)  # 求条件熵
        mutual_info = entropy - conditional_entropy  # 互信息量
        if (mutual_info > max_mutual_info):
            #比较每个特征的信息增益比，只要最好的信息增益比
            max_mutual_info = mutual_info
            best_feature = i
    return best_feature

5. 创建一个majority_vote方法将传入的数据按出现的频率进行降序排列，并返回第一个键名。

def majority_vote(class_list):
    class_count = {}        #存各种分类出现的频率
    for vote in class_list:
        if vote not in class_count.keys():
            class_count[vote] = 0
        class_count[vote] += 1
    #对字典进行排序
    sort_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
    # 排序来决定该节点的类
    return sort_class_count[0][0]

6. 最后一步，根据得到的最优信息增益比生成决策树。

#生成决策树
def create_tree(dataSet, labels):
    class_list = [example[-1] for example in dataSet]
    #终止条件1：class_list是否纯净（纯净就是数据中所有特征都相等）
    if class_list.count(class_list[0]) == len(class_list):
        #当整个数据中的类别完全相同时类别已经纯净了，则停止继续划分，直接返回该类的标签
        return class_list[0]
    if len(dataSet[0]) == 1:
        # 节点已没有特征可以继续分解
        return majority_vote(class_list)
    best_feature = choose_best_feature(dataSet)#选择最好的分类特征索引
    best_feature_label = labels[best_feature]#获得该特征的名字
    #直接使用字典变量来存储树信息
    my_tree = {best_feature_label: {}}     #当前数据集选取最好的特征存储在best_feature中
    del (labels[best_feature])
    # 删掉已选择的特征
    feature = [example[best_feature] for example in dataSet]    #取出最优列的值
    feature_class = set(feature)
    #根据这个列的这个feature_class值来切分树的节点
    for value in feature_class:
        sublabels = labels[:]
        my_tree[best_feature_label][value] = create_tree(remove_feature(dataSet, best_feature, value), sublabels)
        # 迭代生成决策树
    return my_tree

运行结果为：

此决策树共进行四次分类，分别是：“stature”，“hair”，“weight”，“gender”。
ID3算法是由根节点通过计算信息增益选取最合适的属性进行分裂，若新生成的结点的分类属性不唯一，则对新生成的结点继续进行分裂，不断重复此步骤，直到所有样本属于同一类，或者达到要求的分类条件为止。