深度森林目标
| 目标:解决深度学习是否可以用不可微模块实现的问题 |
| 笔记: 1、什么是可微分模块? 在深度学习中,尤其是基于神经网络的模型中,“可微分”是一个非常重要的概念。它指的是模型的输出相对于其参数的导数是存在的且可以计算的。这个特性使得我们能够利用梯度下降等优化算法来训练模型,即通过不断调整参数,使得模型的输出与真实值之间的误差最小化。 神经网络之所以成功,很大程度上归功于其可微分的特性。 神经网络中的每个神经元都执行一个简单的数学运算,这些运算都是可微分的。通过将这些可微分的运算层层叠加,就构成了一个复杂的神经网络。 2、什么是非可微分模块? 与可微分模块相反,非可微分模块是指其输出相对于输入或参数的导数不存在或难以计算的模块。这些模块通常涉及到一些离散的操作、搜索过程或符号运算,这些操作在数学上是不可微的。 常见的非可微分操作包括:
离散化操作举例:
搜索和优化问题举例:
符号运算: 符号运算是指对数学表达式中的符号进行操作,而不是对具体的数值进行计算。这些符号可以代表变量、常数、函数等。在符号运算中,我们关注的是表达式的结构和变换,而不是求得一个具体的数值结果。符号代表的是一个概念,而不是一个具体的数值。对于符号的操作,我们很难定义一个连续的、可导的函数。 |
gcForest
| 深度神经网络中的表征学习主要通过逐层处理原始数据中的特征来实现。 |
| 笔记: Representation learning (表征学习):
Deep neural networks (深度神经网络):
Layer-by-layer processing (逐层处理):
Raw features (原始特征):
深度神经网络通过逐层堆叠多个隐藏层,来对原始数据进行逐层处理。每一层都会学习到比上一层更抽象、更复杂的特征。最终,通过这些层层递进的特征提取,神经网络可以学习到对任务有用的高层语义特征,从而实现对数据的准确分类或预测。 举个例子: 假设我们要训练一个神经网络来识别猫的图片。
|
接下来讲gcForest的级联森林结构,先补充几个概念。
信息增益 |
| 信息增益(Information Gain)用于衡量一个特征对于分类任务的重要性。简单来说,它告诉我们使用某个特征来划分数据集能够带来多少信息增益,也就是能够让数据集变得多“纯”。 举个例子: 你有一堆水果,你需要根据颜色、形状等特征来将它们分类。信息增益就像一个工具,可以帮你找出哪个特征最能有效地将水果分到正确的类别中。 信息增益越大,说明使用这个特征进行划分后,数据集的纯度提高得越多,这个特征也就越重要 在决策树算法中,我们通常选择信息增益最大的特征作为节点的划分属性。这样可以保证每次划分都能最大程度地减少数据集的不确定性,从而构建出更准确的决策树。 |
决策树 |
| 决策树通过一系列规则对数据进行分类或回归。其结构就像一棵树,从根节点开始,通过分支节点不断向下延伸,最终到达叶子节点。每个节点代表一个属性测试,每个分支代表一个测试结果,而叶子节点则对应于最终的分类结果或数值。 决策树的工作原理:
举个例子: 假设我们想要根据天气情况来决定是否打球。 我们收集了一些历史数据,包括天气(晴天、阴天、雨天)、温度(高、低)、湿度(高、低)以及是否打球(是、否)。 构建决策树
最终得到的决策树可能如下:
解释决策树:
|
随机森林:由决策树构成的强大集成学习算法 | ||||||||||
| 什么是随机森林: 随机森林(Random Forest)是一种集成学习方法,它通过构建多棵决策树,并对这些树的预测结果进行投票表决(分类)或取平均值(回归)来实现最终的预测。 随机指的是在构建每棵决策树的过程中,会引入随机性,以减少过拟合的风险并提高模型的泛化能力。 (核心思想就是多棵决策树投票表决) 随机森林的工作原理:
随机森林的优点:
|
完全随机树森林 | |||||||||
| 完全随机树森林(Fully Random Forest,FRF)是随机森林(Random Forest,RF)的一种变体。它在构建决策树时引入了更强的随机性,使得模型具有更强的泛化能力,同时也降低了过拟合的风险。
|
级联森林结构
|
级联森林结构示意图 | |||||||||||||||
| 原文:假设级联的每一层由两个随机森林(黑色)和两个完全随机树森林(蓝色)组成。假设有三个类别需要预测;因此,每个森林将输出一个三维类别向量,然后将其连接起来,重新表示原始输入。 级联森林是一种层次化的集成模型,它结合了随机森林和完全随机树森林的优点,通过多层决策来提高分类和回归性能。 过程:
级联森林的工作原理:
举例: 假设我们想要训练一个模型来识别手写数字(0-9)。 级联森林的方法:
级联森林方法为什么效果好:
|
应用级联森林分析"鸢尾花数据集"的代码实例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn import tree
from sklearn.inspection import DecisionBoundaryDisplay
from matplotlib.animation import FuncAnimation
from sklearn.tree import plot_tree # 导入更直观的决策树可视化函数
# 加载鸢尾花数据集
"""
load_iris() 加载鸢尾花数据集,这是一个经典的分类数据集。
X 存储特征,即鸢尾花的各种测量值。
y 存储标签,即鸢尾花的种类。
"""
iris = load_iris()
X = iris.data
y = iris.target
# 划分训练集和测试集
"""
train_test_split 将数据集随机分为训练集和测试集,其中测试集占20%。
random_state=42 用于保证每次运行时划分结果一致,方便复现。这个参数的作用是 设置随机数生成器的种子,从而使得每次运行代码时,产生的随机数序列都是相同的。
"""
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建级联森林
def create_cascade_forest(X_train, y_train, n_estimators=3, max_depth=5, n_cascade_layers=3):
"""
创建一个级联森林分类器
参数:
X_train: 训练集特征
y_train: 训练集标签
n_estimators: 每个随机森林中的树的数量
max_depth: 每棵树的最大深度
n_cascade_layers: 级联层的数量
返回:
一个列表,包含每一层的随机森林分类器
"""
cascade_forest = []
for i in range(n_cascade_layers):
rf = RandomForestClassifier(n_estimators=n_estimators, max_depth=max_depth, random_state=i)
"""
RandomForestClassifier: 这是一个随机森林分类器。
n_estimators: 每个随机森林中树的数量。
max_depth: 每棵树的最大深度。
random_state=i: 每个随机森林的随机种子设置为 i,保证每次创建的随机森林都不完全相同。
"""
rf.fit(X_train, y_train)
"""
使用训练数据 X_train 和 y_train 来训练当前层的随机森林。
"""
cascade_forest.append(rf)
"""
将训练好的随机森林添加到 cascade_forest 列表中,这个列表用来存储每一层的随机森林。
"""
X_train = rf.predict_proba(X_train)
"""
rf.predict_proba(X_train): 使用当前层的随机森林对 X_train 进行预测,得到每个样本属于各个类别的概率。
X_train = ...: 将上一层随机森林的预测概率作为下一层的输入特征。
也就是说,下一层的随机森林并不是直接对原始特征进行训练,而是对上一层模型预测得到的概率分布进行训练。
"""
return cascade_forest
# 创建一个三层级联森林
cascade = create_cascade_forest(X_train, y_train)
# 可视化所有层的所有决策树
"""
enumerate(cascade):对 cascade 列表进行枚举,同时返回索引 layer_idx 和对应的随机森林 rf。
plt.subplots():创建一个新的绘图区域。
nrows=1, ncols=len(rf.estimators_):设置绘图区域的行数为1,列数等于当前层随机森林中的树的数量。
figsize=(20, 10):设置绘图区域的大小。
enumerate(rf.estimators_):对当前层随机森林中的所有树进行枚举,同时返回索引 tree_idx 和对应的决策树 estimator。
plot_tree():使用 sklearn.tree 模块中的 plot_tree 函数绘制决策树。
feature_names=iris.feature_names:设置特征的名称。
class_names=iris.target_names:设置类别的名称。
filled=True:用颜色填充节点。
ax=axes[tree_idx]:将决策树绘制到指定的子图中。
axes[tree_idx].set_title 设置标题: 为每个子图设置标题,表示这是第几层中的第几棵树。
"""
def visualize_all_trees(cascade):
for layer_idx, rf in enumerate(cascade):
fig, axes = plt.subplots(nrows=1, ncols=len(rf.estimators_), figsize=(20, 10))
for tree_idx, estimator in enumerate(rf.estimators_):
plot_tree(estimator, feature_names=iris.feature_names,
class_names=iris.target_names, filled=True, ax=axes[tree_idx])
axes[tree_idx].set_title(f"Tree {tree_idx+1} in Layer {layer_idx+1}")
plt.show()
# 可视化决策边界动画(仅适用于二维数据)
def visualize_boundary_animation(cascade, X, y):
fig, ax = plt.subplots()
ax.scatter(X[:, 0], X[:, 1], c=y, s=30, edgecolor="k")
def update(frame):
clf = cascade[frame]
disp = DecisionBoundaryDisplay.from_estimator(
clf, X, response_method='predict', alpha=0.5, ax=ax
)
disp.ax_.set_title(f"Decision Boundary of Layer {frame+1}")
return disp,
anim = FuncAnimation(fig, update, frames=len(cascade), interval=1000)
plt.show()
# 可视化所有层的所有决策树
visualize_all_trees(cascade)
# 可视化决策边界动画(将X限制为二维数据)
X_2d = iris.data[:, :2] # 只取前两个特征
visualize_boundary_animation(cascade, X_2d, y)每个随机森林中树的数量为3时,分类结果:




每个随机森林中树的数量为100时,分类结果:



构建级联森林
| 每一层级由决策树森林的集成构成。 多样性对于集成构建至关重要,引入不同类型的森林以促进多样性。 简化情况,使用两种完全随机树森林和两种随机森林。 每个完全随机树森林包含500棵完全随机树,通过在树的每个节点随机选择一个特征进行分裂,并一直生长树直到每个叶子节点仅包含同一类实例。 每个随机森林包含500棵树,通过随机选择√d个特征作为候选(d为输入特征的数量)并选择具有最佳基尼值的特征进行分裂。 每个森林中的树的数量是一个超参数。 |
为什么集成学习中多样性至关重要?
比喻:你想要预测明天的天气。如果你只听取了一个气象专家的意见,那么预测的准确性可能不高。但是,如果你听取了多个气象专家的意见,综合考虑他们的观点,那么预测的准确性就会大大提高。 如何实现多样性?
文章中的例子实现多样性的方式:使用了两种不同类型的决策树森林:
|
随机森林举例:
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn import tree
import seaborn as sns
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建随机森林分类器
rf = RandomForestClassifier(n_estimators=100, max_depth=3, random_state=42)
# 训练模型
rf.fit(X_train, y_train)
# 进行预测并评估
y_pred = rf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
# 可视化混淆矩阵
sns.heatmap(confusion_matrix(y_test, y_pred), annot=True, fmt='d')
plt.xlabel('Predicted')
plt.ylabel('True')
plt.title('Confusion Matrix')
plt.show()
# 可视化第一棵决策树
plt.figure(figsize=(12,8))
tree.plot_tree(rf.estimators_[0], filled=True)
plt.show()

test集混淆矩阵

随机森林中的一棵决策树
决策树解释:
- x[i]。鸢尾花数据集有四个特征:萼片长度、萼片宽度、花瓣长度、花瓣宽度。因此,x[3]就代表了所有样本的花瓣宽度。
- gini指数。随机森林中的每棵决策树在分裂节点时,都会计算不同特征的Gini指数,选择Gini指数增益最大的特征作为分裂特征。Gini指数衡量了节点中样本的纯度,Gini指数的取值范围在0到1之间。Gini指数越小,表示节点的纯度越高,纯度越高的节点,分裂的意义就越小。通过最小化Gini指数,随机森林可以构建出更准确的分类模型。
- samples。随机森林在构建每棵决策树时,会从原始数据集中有放回地随机抽取一部分样本作为训练集。这个随机抽取的过程被称为bootstrap sampling。samples=74,这意味着在构建这棵特定的决策树时,算法随机抽取了74个鸢尾花样本作为初始训练集。
- value。???value数组就是用来记录每个节点中不同类别样本数量的。???为什么74个样本,value里面样本和为120,即为总的训练集数量。为什么从根节点就分类好了???
完全随机森林举例:
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.tree import plot_tree
# 直接从sklearn加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建完全随机森林分类器
model = ExtraTreesClassifier(n_estimators=100, random_state=42)
# 训练模型
model.fit(X_train, y_train)
# 进行预测
y_pred = model.predict(X_test)
# 评估模型性能
print("Accuracy:", accuracy_score(y_test, y_pred))
print("\nClassification Report:\n", classification_report(y_test, y_pred))
# 混淆矩阵
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, fmt="d")
plt.title('Confusion Matrix')
plt.xlabel('Predicted')
plt.ylabel('True')
plt.show()
# 特征重要性
importances = model.feature_importances_
indices = np.argsort(importances)[::-1]
feature_names = iris.feature_names
# 强制转换为整数,确保长度一致
indices = indices.astype(int)
# 可视化特征重要性
plt.figure(figsize=(12,8))
plt.title("Feature Importances")
plt.bar(range(X.shape[1]), importances[indices],
color="r", align="center")
plt.xticks(range(X.shape[1]), [feature_names[i] for i in indices]) # 使用列表推导式
plt.xlim([-1, X.shape[1]])
plt.show()
# 可视化随机森林中的第一棵决策树
plt.figure(figsize=(20,10))
plot_tree(model.estimators_[0], feature_names=iris.feature_names,
class_names=iris.target_names, filled=True)
plt.show()
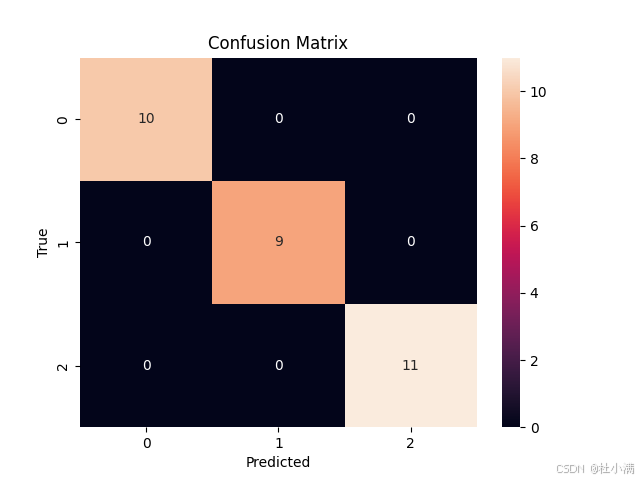
test集混淆矩阵
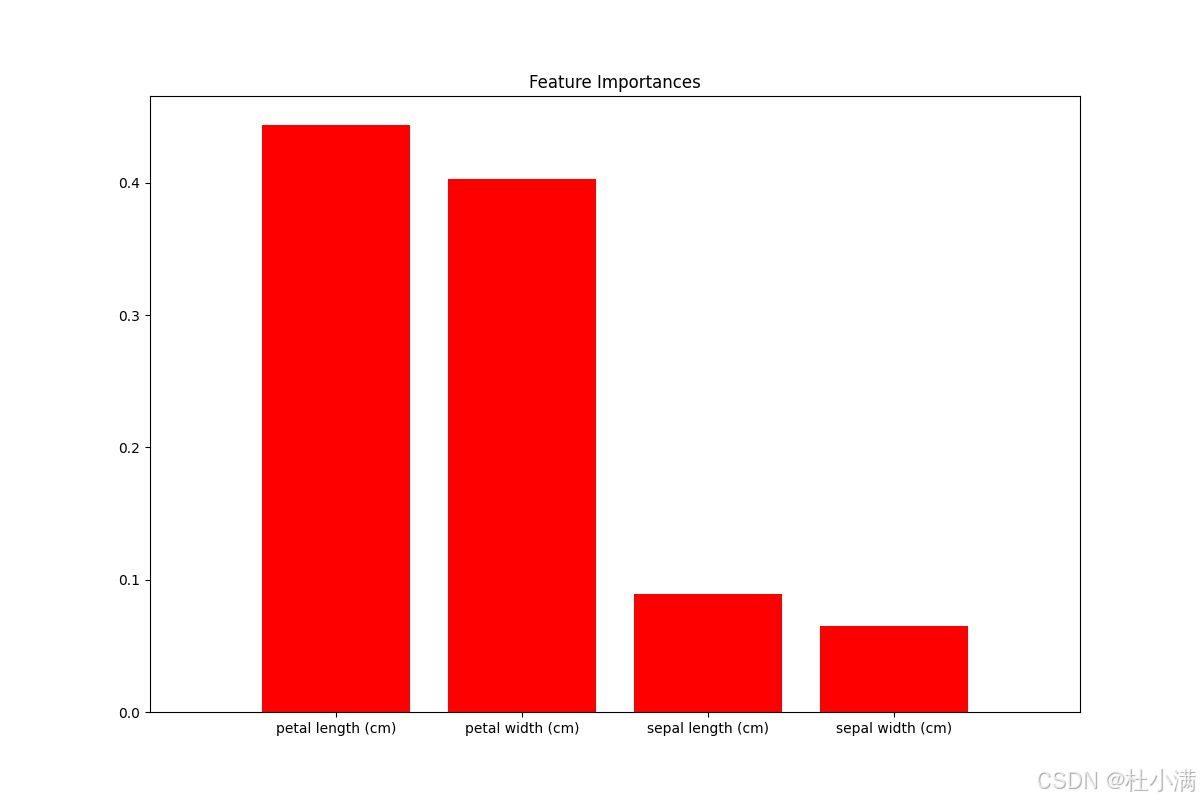
特征重要性

完全随机森林中的一棵决策树
级联
构建过程:
|
图1
图2 类别向量生成过程示例。 叶节点中不同类别的样本比例反映在类别向量中,作为下一层级分类器的输入 |
| 首先,根据训练集,生成了一个森林,假设森林里有500棵决策树。 对于训练集里的一个样本A,假设A落在了决策树1的一个叶子节点里,该叶子节点的类别分布是[0.2 0.5 0.3]。A也落在了决策树2的一个叶子节点里,该叶子节点的类别分布是[0.3 0.4 0.3]。...... A也落在了决策树500的一个叶子节点里,该叶子节点的类别分布是[1.0 0.0 0.0]。 那么,对于森林来说,样本A的类别向量就等于它所在的决策树的叶子节点的类别分布的平均值,为[0.5 0.3 0.2]。 类别分布的含义: 假设一个叶子节点中包含了10个样本,其中有6个属于类别A,3个属于类别B,1个属于类别C。那么,这个叶子节点的类别分布就是:
类别向量的含义: 例如样本A在某个森林的类别向量为[0.5 0.3 0.2],即认为该森林认为样本A有50%的概率是1类,30%的概率是2类,20%的概率为3类。 特征增强: 假设样本A原始特征有m个。 第一级的一个森林给出样本A的一个类别向量[0.5 0.3 0.2],则在下一级中,该类别向量[0.5 0.3 0.2]会成为样本A的新的3个特征,即第二级样本A有m+3个特征。 同理,第一级有4个森林,则第一级会给样本A增加4*3=12个新的特征。每一级都产生12个新特征,也就是说,从第二级开始,样本A的输入特征变为m+12个特征。 自动确定级联层级: 在扩展新层级后,整个级联的性能将在验证集上进行评估,如果性能没有显著提升,则训练过程将终止;因此,级联层级的数量自动确定。 |
多粒度扫描
|
图3 使用滑动窗口扫描的特征重新表示。 假设有三个类,原始特征是400-dim,滑动窗口是100-dim。
图4 gcForest的整个过程。 假设有三个类要预测,原始特征是400-dim,并且使用三种大小的滑动窗口。 |
| 1、特征变换(进入级联森林前) 如图3所示。
2、多粒度特征变换+级联训练 如图4所示。
|






























 1302
1302

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








