用matlab解决简单的数学问题

1 微分和积分

        微分和积分是数学计算中常用的手段。微积分最重要的思想就是”微元“与”逐次逼近“，一个整体的事物往往不好研究，但是通过微元分割成一下块一小块的，当做常量处理，最终加起来就能实现运行效果。在matlab中实现函数微分使用diff函数，实现函数积分使用int函数，其函数具体参数如下：

•  Y= diff(X，n，dim)是沿dim指定的维计算的第n个差分。dim输入是一个正整数标量。 
• Y=integral(fun，xmin，xmax)使用全局自适应积分和默认误差容限在xmin至xmax间以数值形式为函数fun求积分。 

具体代码如下： 

% 微分
syms x
y=3*x^3-6*x^2+5*x+2; % 定义函数
diff(y,x,1)          % 一阶微分
diff(y,x,2)          % 二阶微分
diff(y,x,3)          % 三阶微分
%% 
% 积分
syms x
y=3*x^3-6*x^2+5*x+2; % 定义函数
int(y)               % 求不定积分
int(y,3,4)           % 求定积分
int(y,'a','b')       % a、b为上下限的定积分

运行结果如下图：

 

         diff可以实现函数的各阶微分，同时如果输入为一组向量，则可以计算向量差分结果；integral函数在matlab中可以直接使用int代替，既可以求定积分、不定积分也可以计算无穷积分。

2 数值统计

        对于一组数据，如果我们想分析它的统计特性，发现它的分布规律，我们会使用均值和方差描述一组数据在概率空间中的分布情况。在matlab中实现均值使用mean，实现方差使用var，标准差使用std，其函数具体参数如下：

•  M=mean(A)返回 A 沿大小大于 1 的第一个数组维度的元素的均值。
• V=var(A)返回A沿大小大于1的第一个数组维度计算的元素的方差。默认情况下，方差按N-1实现归一化，其中N是观测值数量。
• S = std(A)返回 A 沿大小大于 1 的第一个数组维度计算的元素的标准差。默认情况下，标准差按 N-1 实现归一化，其中 N 是观测值数量。 

 具体代码如下：

%% 
% 数值统计
A=[1 2 3 4 5 6]      % 输入序列
mean_A=mean(A)       % 求均值
var_A=var(A)         % 求方差
std_A=std(A)         % 求标准差

运行结果如下图：

        用mean、var、std函数可以实现均值、方差、标准差的计算。不仅可以计算向量的统计特性，也可以计算矩阵的各行各列均值、方差、期望等。对于两组不同向量也可以计算相关系数。

3 插值和拟合

        插值是一种数学和计算方法，用于在给定数据点或数值之间估计未知的中间数值。插值的目标是在已知数据点的范围内，通过构建一个函数或曲线，预测或估计在这些点之间的数值。这有助于填补数据的缺失，平滑曲线，以及在实验或测量中获取的离散数据点之间进行更精确的估计。在数学和统计学中，拟合是指通过一个数学模型或函数来逼近或适应一组观测到的数据点。拟合的目标是找到一个函数，使得该函数与观测数据的差异最小化，从而能够表示数据的总体趋势或模式。在matlab中可以直接使用interp1函数进行插值，polyfit进行数据拟合，使用polyval返回插值点的函数值，其函数具体参数如vq

• vq= interp1(x,y,vq) 使用线性插值返回一维函数在特定查询点的插入值。向量 x 包含样本点，v 包含对应值v(x)。向量 xq 包含查询点的坐标。
• p = polyfit(x,y,n) 返回次数为 n 的多项式 p(x) 的系数，该阶数是 y 中数据的最佳拟合（基于最小二乘指标）。p 中的系数按降幂排列，p 的长度为 n+1。主要用来返回拟合多项式的系数，
• y = polyval(p,x) 计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量，其元素是 n 次多项式的系数（降幂排序）。主要用来输入x的向量，返回对应的函数值向量。  

具体代码如下：

%% 
% 插值
x=[0, 1, 2, 3];    % 输入自变量x
y=[1, 4, 9, 16];   % 输入因变量y
xi=0:0.1:3;        % 确定插值范围
yi=interp1(x, y, xi); % 进行函数插值
plot(x, y, 'o', xi, yi,'*') % 绘制插值图像
%% 
% 拟合
x=linspace(0,4*pi,10); % 输入自变量x
y=sin(x);              % 输入因变量y
p=polyfit(x,y,7);      % 对x、y用7次函数进行拟合
x1=linspace(0,4*pi);   % 输入插值范围点
y1=polyval(p,x1);      % 输出对应插值值
figure                   % 创建画布
plot(x,y,'o',x1,y1)      % 对原数据及插值结果进行绘制

运行结果如下图：

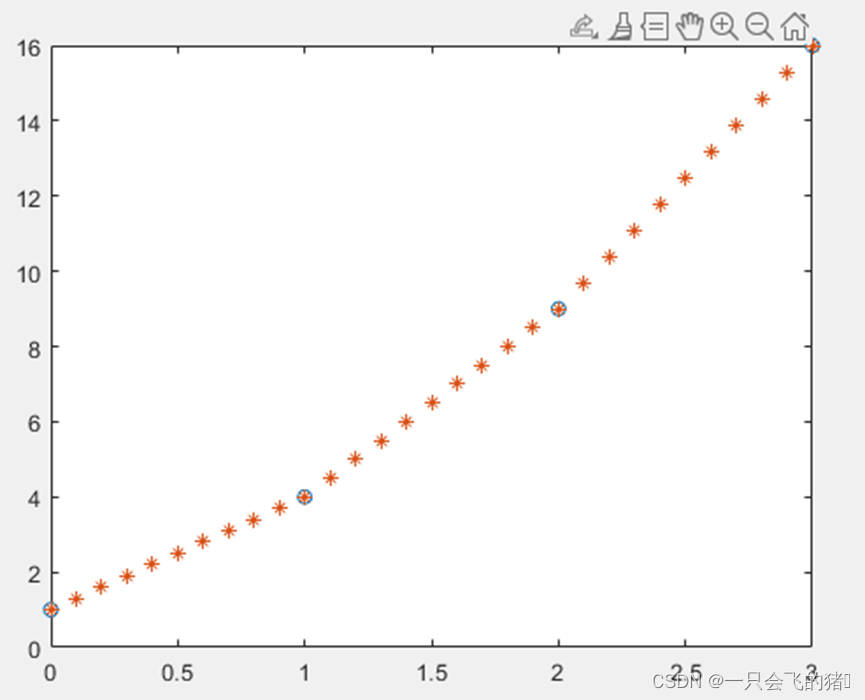
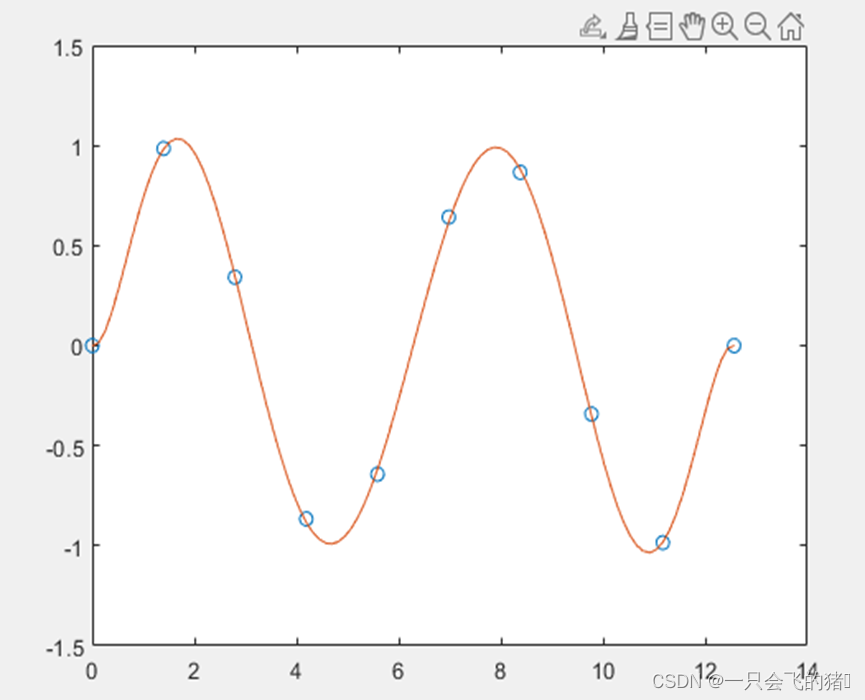
        插值可以在有限数据中产生更多的数据点，拟合主要是将离散的数据点拟合成连续的曲线，然后可以在对应需要的点的位置取出函数值。在拟合中往往不同阶数拟合结果不同，往往阶数越高拟合效果越好，对于同一问题的不同阶数拟合的代码段和结果如下： 

function[]=nihe()
clc;
clear all;
date1=load("data.txt");
x=date1(:,1);
y=date1(:,2);
%%%一次拟合
dat=polyfit(x,y,1);
y1=dat(1).*x+dat(2);
%%%二次拟合
dat2=polyfit(x,y,2);
y2=dat2(1).*x.*x+dat2(2).*x+dat2(3)
% polyval(dat2,x)
%%%三次拟合
dat3=polyfit(x,y,3);
y3=dat3(1).*(x.^3)+dat3(2).*(x.^2)+dat3(3).*x+dat3(4);
n=16;
datn=polyfit(x,y,n);
yn=0;
for i=1:1:n+1
    yn1=datn(i).*(x.^(n+1-i));
    yn=yn1+yn;
end
plot(x,y,'o',x,y1,'r-',x,y2,'b-',x,y3,'g-',x,yn,'k-');
legend('密度线','线性拟合','二次拟合','三次拟合','n次拟合');
dd=[x,y];
save dd.txt dd -ascii
end

 4 线性方程组求解

        线性方程组是一组包含线性方程的方程集合，其中每个方程都是未知数的一次幂与常数的线性组合。求解线性方程组的目标是找到一组未知数的值，使得方程组中的每个方程都得到满足。求解线性方程组往往是通过一系列的行变换来进行求解。对于系数矩阵满秩的方程组，可以通过逆矩阵来进行运算，矩阵的逆表示为inv(A)。

代码段及运行结果如下：

%% 
% 线性方程求解
A=[5 1 4  8;4 3 6 7;2 5 4 3;3 7 5 11]; % 输入方程组系数
B=[3;10;4;9];                          % 输入已知项
X=inv(A)*B                             % 解线性方程组
X=A\B                                  % 解线性方程组
B_1=A*X                                % 验证结果正确性

        该线性方程组的系数矩阵是一个满秩矩阵，其解既可以使用矩阵求逆的方法，也可以使用行变换求解，经过运算两者求解结果一致。同时将运算结果带入方程组可以解出线性方程组对应的常数项，验证结果正确。

5 非线性方程组求解

        非线性方程组是一组方程，其中至少有一个方程包含了非线性项。求解非线性方程组的目标是找到一组对应的值，使得所有的方程都成立。与线性方程组不同，非线性方程组的求解通常更为复杂，因为非线性函数的存在使得无法直接应用类似于矩阵求逆的线性代数技术来解决。常常使用牛顿法、拟牛顿法、迭代法进行运算。在matlab中可以使用fsolve函数进行求解，其函数具体参数如下：

• x = fsolve(fun,x0) 从 x0 开始，尝试求解方程 fun(x) = 0（全零数组）。先将方程组全变为相减为0的形式，通过一个初始的种子去遍历迭代来找到一个同时满足两个方程组的点，即为此非线性方程组的解。

代码段及运行结果如下：

% 定义非线性方程组
function F = root2d(x)
    F(1) = exp(-exp(-(x(1)+x(2)))) - x(2)*(1+x(1)^2);
    F(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5;
end

%% 
% 非线性方程求解
fun=@root2d;           % 获得函数句柄
x0=[0,0];              % 定义种子
x=fsolve(fun,x0)       % 求解

        将种子设置为(0,0)通过不断的迭代缩小范围求出函数的解为0.3532，0.6061，带入非线性方程组验证解的正确性。 

6 常微分方程求解

        常微分方程是描述一个或多个未知函数及其导数之间关系的方程。这类方程中，未知函数仅依赖于一个独立变量，而不涉及多个独立变量的偏导数。求解常微分方程的过程涉及找到满足方程的未知函数y(x)。其求解主要包括求通解和求特解两种，对于同一通解，不同的初值会产生不同的特解。在matlab中使用dsolve函数进行常微分方程求解，其函数具体参数如下：

S=dsolve(eqn,cond,Name,Value) eqn为给定的常微分方程(组)，Value为给定的常微分方程(组)的指定符号自变量，默认变量为t。cond1,cond2,…为给定的常微分方程(组)给定的边界条件(或初始条件)。

代码段及运行结果如下：

%% 
% 常微分方程求解
dsolve('Dy=3*x^2','x')   % 求通解
dsolve('Dy=3*x^2','y(0)=2','x') % 求特解
[x,y]=dsolve('Dx=y,D2y-Dy=0','x(0)=2,y(0)=1,Dy(0)=1') % 求解微分方程组

        常微分方程求通解会产生常数项C，带入初始条件可以解出固定的C，产生对应的特解。求线性方程组时，在matlab常常使用参数t来作为变量。求解参数方程组解出来的结果含有相同的参数t。