数学知识：中国剩余定理

最新推荐文章于 2025-04-05 16:10:52 发布

辰chen

最新推荐文章于 2025-04-05 16:10:52 发布

阅读量1.2k

点赞数 15

分类专栏：基础算法文章标签：算法数学数论中国剩余定理孙子定理

本文链接：https://blog.csdn.net/qq_52156445/article/details/117414509

版权

基础算法专栏收录该内容

108 篇文章

订阅专栏

本文介绍了中国剩余定理的基本概念，并结合AcWing204题——表达整数的奇怪方式，进行了详细解析。通过AC代码展示了如何应用孙子定理解决实际问题，虽然原题并未限制两两互质，但依然可以通过变形求解。遗憾的是，文章暂时未给出时间复杂度的详细分析和证明。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

复习acwing算法基础课的内容，本篇为讲解数学知识：中国剩余定理，关于时间复杂度：目前博主不太会计算，先鸽了，日后一定补上。

一、中国剩余定理

即孙子定理，具体定理即推导见：孙子定理，注意中国剩余定理必须要求两两互质，本博客例题中没有限制两两互质，故不能直接套用中国剩余定理的公式，需要在基础之上进行变形

二、AcWing 204. 表达整数的奇怪方式

本题链接：AcWing 204. 表达整数的奇怪方式
本博客提供本题截图：
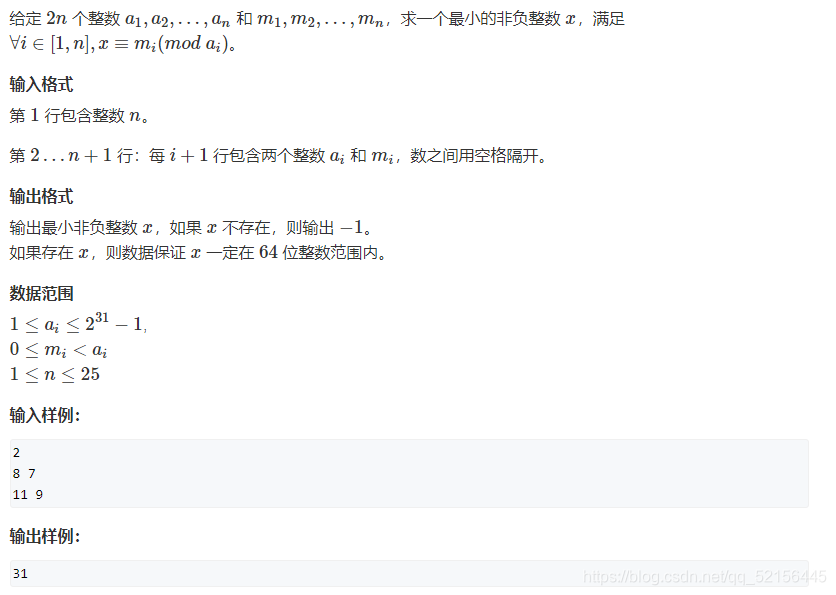
在这里插入图片描述

本题解析

理论推导见OI爷的博客：墨染空 ,

AC代码

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;


LL exgcd(LL a, LL b, LL &x, LL &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }

    LL d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}


int main()
{
    int n;
    cin >> n;

    LL x = 0, m1, a1;
    cin >> m1 >> a1;
    for (int i = 0; i < n - 1; i ++ )
    {
        LL m2, a2;
        cin >> m2 >> a2;
        LL k1, k2;
        LL d = exgcd(m1, -m2, k1, k2);
        if ((a2 - a1) % d)
        {
            x = -1;
            break;
        }

        k1 *= (a2 - a1) / d;
        k1 = (k1 % (m2/d) + m2/d) % (m2/d);

        x = k1 * m1 + a1;

        LL m = abs(m1 / d * m2);
        a1 = k1 * m1 + a1;
        m1 = m;
    }

    if (x != -1) x = (x % m1 + m1) % m1;

    cout << x << endl;

    return 0;
}