写信（单调队列优化）

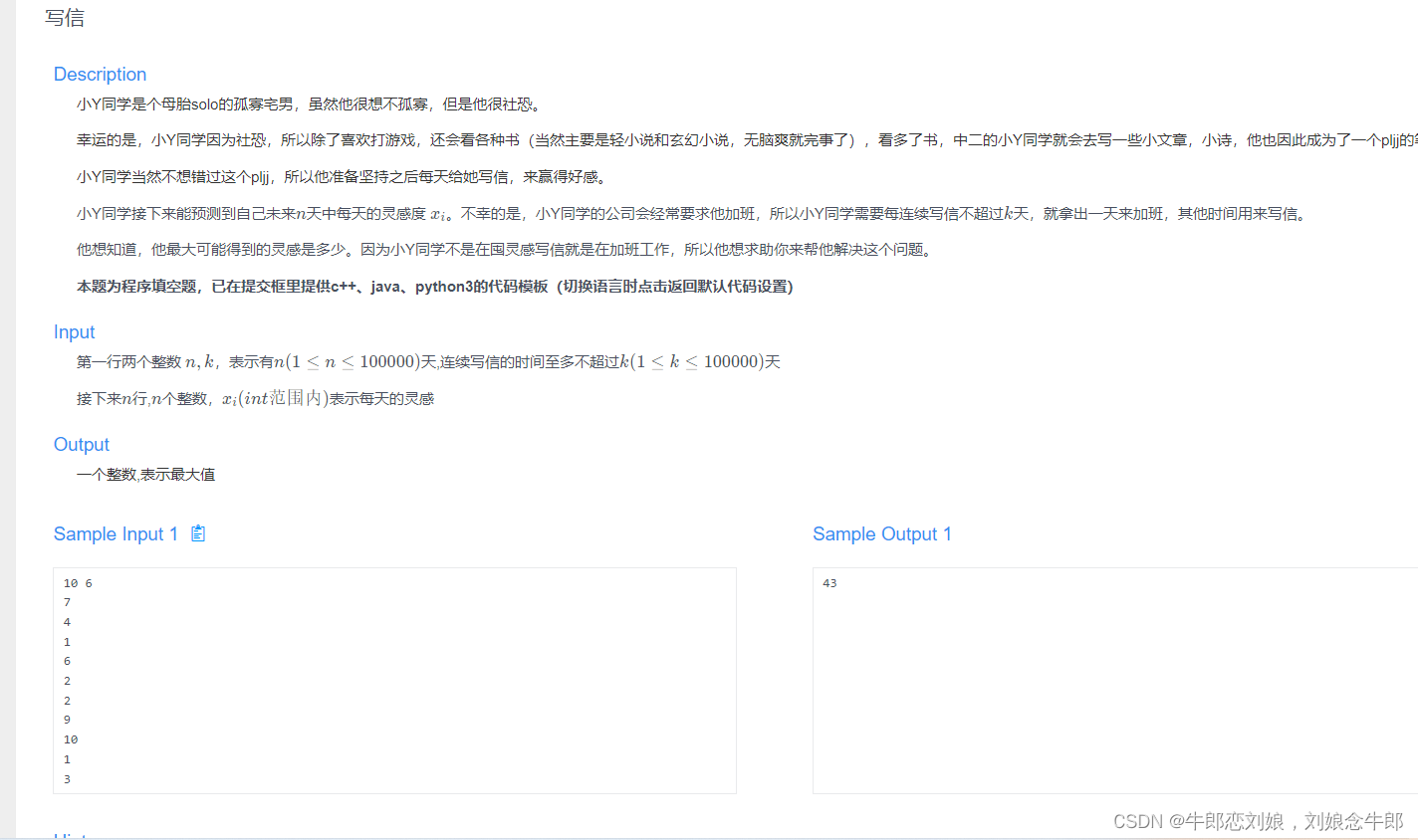
求每隔不超过k个数就必须删去一个数，使得删去数的和最小。
我们设 f[i] 为前i个数中，在一定删除第i个数的情况下，满足上述条件的答案。
那么我们可以得到 f[i] = x[i] + min(f[i - k]…f[i - 1]);
但是按照题目数据范围这样做会超时，所以我们引入一个新得数据结构叫单调队列，对min这个部分进行优化：我们建立一个队列，保证队列是单调递减的，这样我们就可以保证当 f[j] >= f[i] （j >= i）时 f[j]无法入队。

同时我们保证单调队列长度不超过k，那么我们就可以保证题目所说的每不超过k个数删除一个的条件。这样我们每次取队首更新f[i]即可。

在提交的时候发现题目关闭了 这个代码只过了样例

前k个 f[i]=x[i]; 同时维护单调队列

#include<bits/stdc++.h>
using namespace std;
map<int,int>mp;
const int maxn=2e6+100;
//bool number[maxn + 5];
int n,m,k,sum,cnt;
#define PI 3.141592653 
typedef long long ll;
//ll a[1000009],b[1000009];
const int mod=998244353;
const int N=1e6;
typedef pair<int,int> PII;

ll f[1000000];
ll arr[1000000];

int pos[N], que[N];//, MAX[N], MIN[N];

int head = 1, tail = 0;


int main(){
	cin>>n>>k;
	for(int i=1;i<=n;i++){
		cin>>arr[i];
		sum+=arr[i];
	}
	if(k>=n){
		cout<<sum;
		return 0;
	}
	for(int i=1;i<=k;i++){
		f[i]=arr[i];
		while(head <= tail && que[tail] > arr[i]) --tail;//队尾元素 > 当前元素, tail前移至 队尾元素 <= 当前元素//插入 
		que[++tail] = arr[i];
		pos[tail]   = i;
	//	if(i<k) f[i]=arr[i];
	//	else 
		if(i < k) continue;//窗口大小未至 k 
		while(pos[head] < i - k + 1) ++head;//删队头, 因为在滑动过程中, 队头元素会被舍弃 
		//MIN[i - k + 1] = que[head]; 
	}
	for(int i = k+1; i <= n; ++i)
	{
	//	cin>>arr[i];
	//	if(i>=k) 
		f[i]=arr[i]+que[tail];
		
		while(head <= tail && que[tail] > f[i]) --tail;//队尾元素 > 当前元素, tail前移至 队尾元素 <= 当前元素//插入 
		que[++tail] = f[i];
		pos[tail]   = i;
		//if(i<k) f[i]=arr[i];
	//	else 
	//	if(i < k) continue;//窗口大小未至 k 
		while(pos[head] < i - k + 1) ++head;//删队头, 因为在滑动过程中, 队头元素会被舍弃 
	//	MIN[i - k + 1] = que[head]; 
	}
	ll mina=1000000000;
	for(int i=n-k+1;i<=n;i++){
		mina=min(mina,f[i]);
	}
	cout<<sum-mina;
	return 0;
}