Top-k问题————TA, NRA, LARA算法

Top-k问题就是当前有大量数据，每条数据有一个或多个attribute，有一个针对这些变量的aggregate function f，函数output就是combined score，找到score最高或最低的前k个数据。
最简单的例子就是一堆商品信息，找到最贵的2个商品。

普通情形

关于大量数据的Top-k问题，已经有无数文章讨论过，比如TOP-K问题（清晰，巨全）和Top K算法详细解析—百度面试。
网上的最佳答案是HASH+堆。而对于各种变种，这里一篇文章已经讲得很清楚：教你如何迅速秒杀掉：99%的海量数据处理面试题。其中思路也比较值得借鉴。其基本思路就是：能够放到内存中的数据量，则采用bitmap，bloom filter等方法放到内存；不能放到内存中的数据，则分开为小文件或者小节点，每个小文件分别计算，最后汇总计算。

数据库情形

很多时候我们的数据是在数据库中，很多时间已经有index排序某些列，针对这些情况，我们有以下算法利用这种特性进行ranking query。
注意：以下算法都要求aggregate function f 聚合函数是distributive, monotone的
distributive可分配的: f(x,y,z,w)= f(f(x,y),f(z,w))
e.g., A+B+C+D = (A+B) + (C+D)
monotone单调的: if x<y and z<w, then f(x,z)<f(y,w)
e.g., 3 < 5 and 2 < 8 -> 3+2 < 5+8

TA算法(threshold algorithm)

**TA算法（threshold algorithm）**是一种经典的Top-k算法，只能用于支持随机读取数据的环境，要求distributive, monotone。
算法流程：

1. 该算法需要先对聚合函数涉及到的attributes都进行1-dimension（1-D）排序，排序顺序得看该列对函数是递增还是递减的以及求得分小还是大，但总之排序靠前越容易得出我们想要的k项，我们排序后有几个表，每个表对应涉及的一个attribute，虽然顺序打乱了但我们还是知道某个表的某一项和另一个表的哪一项原本是一行数据里的，将这些排序后的表看成是一个表。
2. 不断对排序后的表从头开始遍历，一行为一轮，每一轮计算出该行的score聚合函数得分T，该行并不真的存在，对该行中每一attributes找到其对应的真实数据（随机读取），计算这些真实行的得分，保存得分最大/最小的前k项数据，求得分大就保存大的。
3. 遍历停止条件：当该轮中得分T小于/大于之前计算保存的第k项数据得分时，遍历停止，输出前k项数据，求得分大的就是小于。

解析：以求最大得分k项为例。我们对各个attributes排序后，聚合函数（monotone）得分高的肯定是有attribute排序前列的，以单调递增为例，attribute大才得分高，我们查询了有某attribute大的所有行，而遍历的T肯定是理想情况，停止时，排序表当前行的T中所含attribute的所属行要么查询过了（所属行的其他attribute很大之前出现过），要么没查询，没查询的情况是所属行其他attributes小于当前遍历的排序表的值，那该所属行得分一定小于该T，而T小于第k项得分，所属行得分比第k项低，不用记，以此类推，之后所有查询行都会低于第k项，当然就停止了。
Example:
图中a、b、c…代表原本所属同一行真实数据

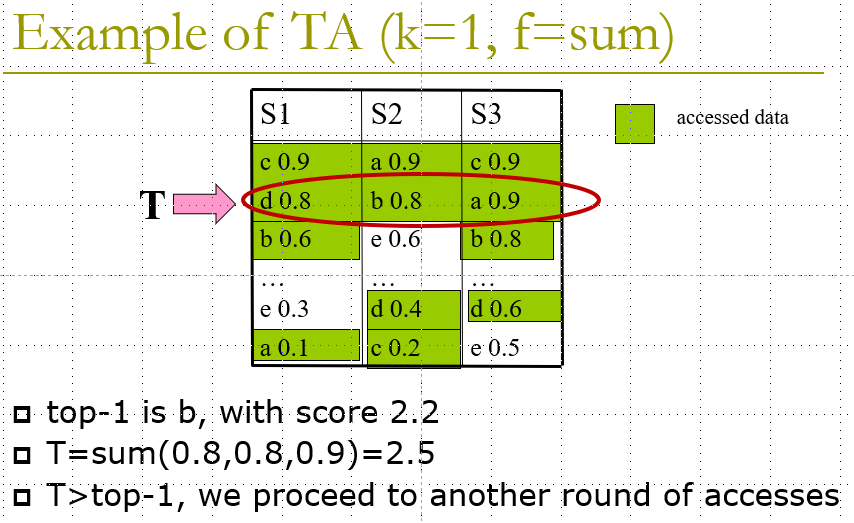
NRA(No Random Access)

很多时候random access成本很高或者不支持随机读取，那就需要NRA算法，算法要求distributive, monotone。
算法流程：

1. 就像TA算法。该算法需要先对聚合函数涉及到的attributes都进行1-dimension（1-D）排序，排序顺序得看该列对函数是递增还是递减的以及求得分小还是大，但总之排序靠前越容易得出我们想要的k项，我们排序后有几个表，每个表对应涉及的一个attribute，虽然顺序打乱了但我们还是知道某个表的某一项和另一个表的哪一项原本是一行数据里的，将这些排序后的表看成是一个表。
2. 不断对排序后的表从头开始遍历，一行为一轮，每一轮对该行中每一attributes找到其对应的真实行ID，将该真实行ID放入待计算list，计算这些真实行的最大可能得分和最小可能得分，毕竟不能随机读取计算不出真实得分，每轮都得重新计算待计算list中的真实行。而每轮待计算list中最小可能得分较大的前k个真实行视为该轮的目标list。待计算list中最大可能得分比目标list所有最小可能得分小的话，后面是可以不用计算了，毕竟没可能大了。
   
   以求最大k项、单调递增所以降序为例：
   最大可能得分=已知的该真实行的列值+未知列对应排序表的已遍历的最小值。因为未知列还没出现只能比排序表中已扫描的值小，最大可能性也不能大于加上排序表最小值的情况。
   最小可能得分=已知的该真实行的列值+0（默认）或最小可能得分=已知的该真实行的列值+未知列对应排序表最小值（含负数情况），这里不确定对不对，老师只用默认情况。
3. 遍历停止条件：
   以求最大k项、单调递增所以降序为例：
   取出该轮目标list里最小可能得分最小的真实行，取出未在目标list但待计算list里最大可能得分最大的真实行，若前者最小可能得分比后者最小可能得分还大，则停止并输出目标list中真实行，这就是前k项。
   注意：有可能得到前k项结果但并没有实际上遍历到所有attribute值，也就是可能还没得到真实得分。

Cost: O(n) per access (the expected distinct number of objects accessed so far is O(n))

解析：以求最大得分k项为例。我们对各个attributes排序后，聚合函数（monotone）得分高的肯定是有attribute排序前列的，以单调递增为例，attribute大才得分高，最小可能得分都比别的行最高得分高了，那肯定是前k项最高的了。

Example:
图中a、b、c…代表原本所属同一行真实数据，Wk就是k项目标list

LARA(Attice-based Rank Aggregation)

LARAL是NRA的改良版本，所以无需random access，算法要求distributive, monotone。
对NRA的观察：
以下以求最大k项、单调递增所以降序为例
如TA一样令T=每一轮遍历到的排序表的该行的score聚合函数得分。易得NRA里每轮中，所有还没进入待计算list的真实行的得分一定比T低。毕竟还没进的真实行的所有attributes值都比该行低。
令t=每一轮的目标list中最小的最小可能得分。

• Observation 1：当t<T时，后面进入待计算list的真实行有可能是我们要的top-k的一项。
• Observation 2：当t<T时，此时待计算list里的真实行都有可能是我们要的top-k的一项。
  注意：不代表t>T时，目标list有哪些行定死了，待计算list里的真实行还是有可能进入目标list。只是说t<T时一定存在Observation 2的情况
• Observation 3：当$t\ge T$时，后面进入待计算list的真实行不可能是我们要的top-k的一项。
  对NRA观察的思考：
  Observation 3是Observation 1的后续，也就是说只有t<T时，进入待计算list的真实行才有可能是我们要的top-k的一项。

1. 也就是说t>T后我们没必要往待计算list里添加candidate了。
2. 也只有$t\ge T$后才需要开始计算最大可能得分去判断停止条件。

算法流程：

1. 就像TA、NRA算法。该算法需要先对聚合函数涉及到的attributes都进行1-dimension（1-D）排序，排序顺序得看该列对函数是递增还是递减的以及求得分小还是大，但总之排序靠前越容易得出我们想要的k项，我们排序后有几个表，每个表对应涉及的一个attribute，虽然顺序打乱了但我们还是知道某个表的某一项和另一个表的哪一项原本是一行数据里的，将这些排序后的表看成是一个表。
2. growing phase（成长期）：不断对排序后的表从头开始遍历，一行为一轮，每一轮对该行中每一attributes找到其对应的真实行ID，将该真实行ID放入待计算list，计算这些真实行的最小可能得分，计算方法和NRA一样，每轮都得重新计算。而每轮待计算list中最小可能得分较大的前k个真实行视为该轮的目标list，得到t和T，判断$t是否\ge T$，若$t\ge T$则进入收缩期

Wk is updated at O(logk) cost after each access (heap implementation). T’s update cost is O(1).

4. shrinking phase （收缩期）：$t\ge T$时进入。虽然继续遍历但不再往待计算list里添加candidate了。开始不断计算待计算list里各行的最大可能得分，最小可能得分也继续算，而每轮待计算list中最小可能得分较大的前k个真实行视为该轮的目标list。取出该轮目标list里最小可能得分最小的真实行，取出未在目标list但待计算list里最大可能得分最大的真实行，若前者最小可能得分比后者最小可能得分还大，则停止并输出目标list中真实行，这就是前k项。

解析： NRA的改良版，改良部分看前文对NRA的观察和思考。

Growing phase: O(logk) per access
Shrinking phase: O(2m+logk) per access
Computational cost is much lower than the O(n) cost of NRA

Example：