基于Lumerical FDTD超透镜仿真的简单案例

已于 2024-10-26 11:54:49 修改
阅读量1w 收藏 159
点赞数 68
文章标签： 经验分享
于 2024-07-24 22:19:28 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_52317002/article/details/140673860
版权

    本文将要介绍的是使用FDTD仿真软件仿真透射式聚焦超透镜的流程。

一、本文的主要工作

1.1 复现一种几何(PB)相位超透镜

    参考文献：基于PB相位的等离子体超透镜设计-夏习成，姚赞。文中采用了在金属膜上刻蚀矩形孔的方法形成一种PB相位超原子。见下图。

图 1

    根据PB相位理论，使用圆偏振入射，出射光中有一部分将会变成相反的手性，并且获得和旋转角度成2倍关系的附加相位。

图 2

1.2 复现一种全电介质几何相位超透镜

    1.1中提到的超透镜在可见光波段聚焦效率不高，因而本文又复现了一种全电介质材料超透镜。

    参考文献：Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging-Mohammadreza Khorasaninejad, Wei Ting Chen,  Robert C. Devlin,   Jaewon Oh, Alexander Y. Zhu, Federico Capasso

    （上面这篇文章来自Capasso课题组，他们在超透镜领域做的工作很好，广义斯涅尔定律就是他们提出来的） 

偏振转化率随波长的变化；左边是原文仿真结果，右边是本文复现结果。

图 3

1.3 一种简单的传播相位超透镜设计及优化

    几何相位（PB相位）要求入射光为圆偏振光。为了解除这种限制，本文利用90°旋转对称的超原子构成偏振不敏感超透镜进行仿真。

图 4

二、超原子设计及优化

2.1 结构生成

    首先构建图1中的超原子，原文中给出的参数为：金膜厚度为40nm；刻蚀孔长215nm,宽60nm。文中没有给出仿真光源的位置以及基底的厚度。一般来说，光源可以距离结构近一些以减小仿真空间，但也要留一定空间方便后续添加光阑、监视器等。

    可以采用图形界面交互或者脚本控制来构建结构。本文先用脚本生成基本结构，再用图形界面交互的方法调整。脚本可以写在右边栏Script File Editor（脚本编辑器）中，也可以写在左边物品栏的结构组中，注意二者会相互冲突。

    下面是一段使用脚本编辑器构建图1中超原子的代码。这段代码包含了基本结构、由两个正交的线偏振光构成的圆偏振光、仿真区域与仿真边界等。此脚本缺少监视器，可以通过图形界面交互的方式给出。(监视器在下面的分析组提及)

nm=1e-09;
um=1e-06;

deleteall;

hight=0.04*um;#金膜及刻蚀孔厚度
lambda=0.6e-6;#光源波长
p=0.35*um;#周期
#基底
addrect;
set("name","substrate");
set("x",0);set("x span",0.4*um);
set("y",0);set("y span",0.4*um);
set("z max",0);set("z min",-0.1*um);
set("material","SiO2 (Glass) - Palik");
#金薄膜
addrect;
set("name","gold-layer");
set("x",0);set("x span",0.4*um);
set("y",0);set("y span",0.4*um);
set("z max",hight);set("z min",0);
set("material","Au (Gold) - Palik");
#添加刻蚀孔
addrect;
set("name","etch");
set("x",0);set("x span",0.215*um);
set("y",0);set("y span",0.06*um);
set("z max",hight);set("z min",0);
set("material","etch");
#添加光源
addplane;
set("name","Source_x");
set("injection axis","z");
set("direction","Backward");
set("plane wave type",1);
set("x",0);set("x span",0.4*um);
set("y",0);set("y span",0.4*um);
set("z",2*hight);
set("wavelength start",lambda);
set("wavelength stop",lambda);

addplane;
set("name","Source_y");
set("injection axis","z");
set("direction","Backward");
set("plane wave type",1);
set("polarization angle",90);set("phase",90);
set("x",0);set("x span",0.4*um);
set("y",0);set("y span",0.4*um);
set("z",2*hight);
set("wavelength start",lambda);
set("wavelength stop",lambda);
#仿真区域
addfdtd;
set("dimension",2);  #  1 = 2D, 2 = 3D
set("x",0);
set("x span",p);
set("y",0);
set("y span",p);
set("z max",0.1*um);
set("z min",-0.8*um);
set("mesh accuracy",2);
set("x min bc",3);  #这里用序号而不是Periodic的名称
set("y min bc",3);
set("z min bc",1);
set("z max bc",1);
#刻蚀孔处划分更细致的网格
addmesh;
set("based on a structure",1);
set("structure","etch");
#规定旋转主轴
setnamed("etch","first axis","z");

2.2 参数扫描

    我们关心的超原子的两个参数：附加相位和透射率。对于PB相位的超原子来说，后者（透射率）即偏振转化率。偏振转化率即和入射光手性相反的那部分出射光的功率和入射光功率之比。

    PB相位超原子的作用类似于半波片，可以用琼斯矩阵推导附加相位的变化。推导过程参考文献《长波红外宽带消色差超透镜研究》-邬灏。结果见下式，理论上附加相位是超原子旋转角度的两倍。

    至于偏振转化率，它是波印廷矢量的面积分与入射光功率之比：

    下面介绍参数扫描的具体流程。 

    扫参有两项：附加相位随旋转角度的变化；偏振转化率随入射光波长的变化。

    1. 分析组及监视器

    相位监视器要使用点监视器，偏振转化率监视器则是面监视器。

图5 分析组

添加监视器后右键可以改变位置，将监视器移到分析组下面看到它自动缩进即可。 

图6 相位监视器和透射率（偏振转化率监视器）放在分析组内 

 附加图1 相位监视器参考参数

 附加图2 透过率监视器参考参数

    2. 定义扫参变量

    需要的扫参变量分别为波长lambda和刻蚀孔旋转主轴rotation1的旋转角度。rotation1在结构构建脚本中已经设定为刻蚀孔etch的旋转主轴，不需要额外定义。以下是定义变量lambda的流程：

    依次点击model>Edit object:

    依次点击setup>variables>add：

    然后切换到script:

    3. 定义扫参结果

    依次点击anlysis group>edit object:

    依次点击analysis>script，处理运行工程文件后产生的数据。

Ex=getdata("phase","Ex");
Ey=getdata("phase","Ey");
E_R=Ex+1i*Ey;
E_L=Ex-1i*Ey;
Phase1=angle(E_R);
Phase2=angle(E_L);#phase1和phase2分别是两种手性出射光的相位

T_1=getresult("T1","T");
T_2=-T_1.T;

f=getdata("T1","f");
x = getdata("T1","x");
y = getdata("T1","y");
Ex = getdata("T1","Ex");
Ey = getdata("T1","Ey");
Hx = getdata("T1","Hx");
Hy = getdata("T1","Hy");

E_r = (Ex - 1i*Ey)/sqrt(2);
E_l = (Ex + 1i*Ey)/sqrt(2);
H_r = (-1i*Hx +Hy)/sqrt(2);
H_l = (1i*Hx + Hy)/sqrt(2);

# 计算波印廷矢量的z分量
Pz_r = E_r*conj(H_l); #复共轭
Pz_l = E_l*conj(H_r);
# 积分
Tr_r=-integrate(real(Pz_r)/2,1:2,x,y)/sourcepower(f); # 在x,y面积分
Tr_l=-integrate(real(Pz_l)/2,1:2,x,y)/sourcepower(f);

    上述代码得到右旋圆偏振出射光的相位phase1和偏振转化率Tr_l以及左旋圆偏振出射光的相位phase2和偏振转化率Tr_r。然后点击variables，在results中添加扫参结果量。

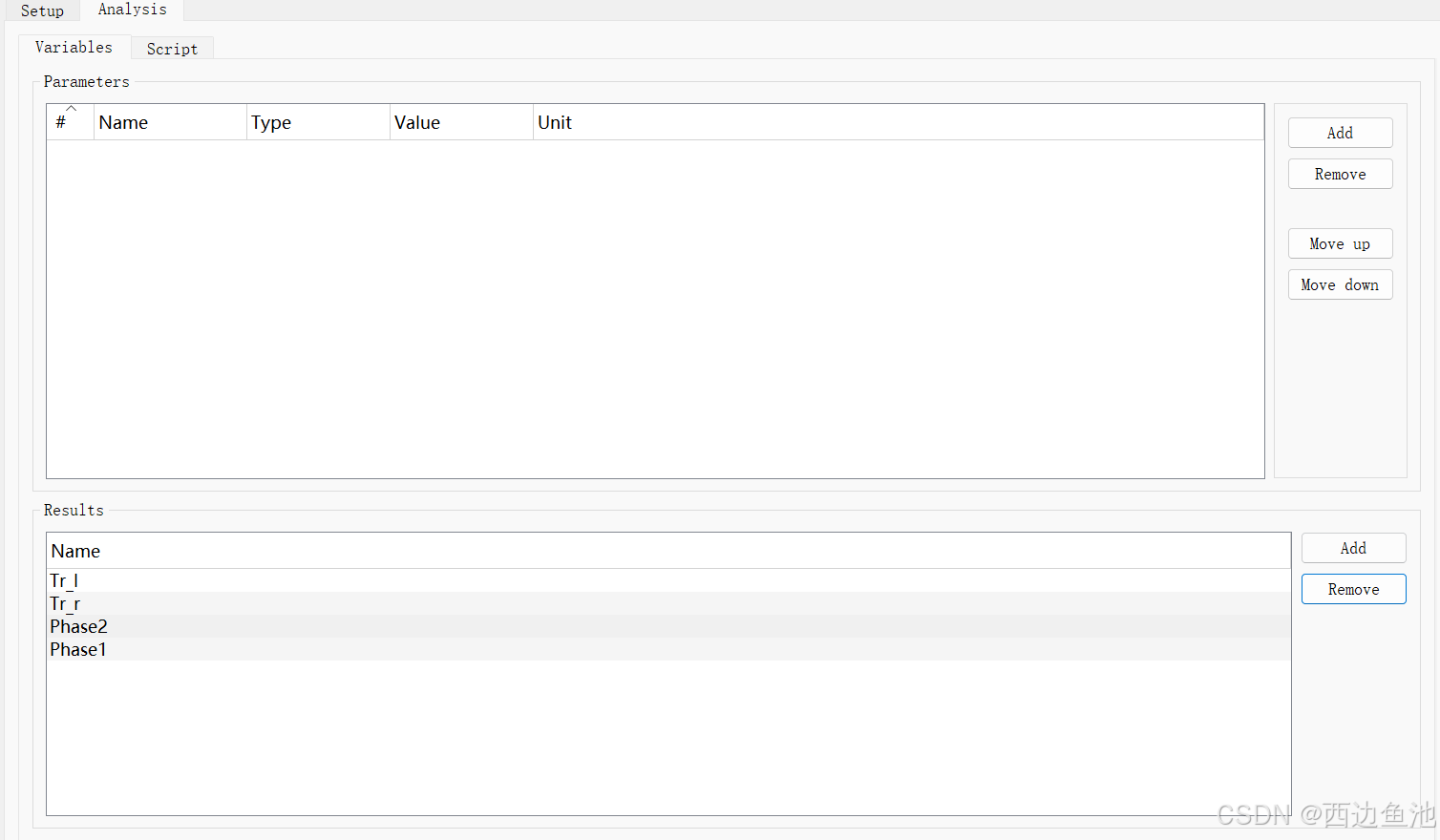
    4. 扫参进程

    扫参可以在右边栏的optimization and sweeps中设置，它一般和脚本在同一个窗口，如果没有可以在view>windows中打开。点击下图框中按钮添加扫参进程。下面两个是对相位和偏振转化率（PCR）扫参的项目。 

   首先示范相位扫参进程设置方法：

   新建一个扫参进程，右击，选择Edit。 

    弹出窗口如下。主要有三部分：命名、参数和结果。

    命名随意设置，方便区分记忆即可。

    Parameters（参数）这一部分，Type可以选择一段范围（Ranges），这样扫参的数据点将根据后面设定的起始值和点的数目（Number of points）均匀划分；或者Type选择数值（Values）,那么具体的扫参数据点需要用户给出。方便起见这里采用前者。

    点击右侧的add，见下图：

    附加相位由结构的旋转引起，这里的参数应是刻蚀孔的旋转角度。

    找到parameter>model>objects>etch，选中rotation1(在结构构建的脚本中已将rotation1设定为z轴的旋转角度)。

     起始数值分别为0和360。可以给参数命名。设置完成界面如下：

     下面设置扫参结果（Results）。在model>objects>analysis group>results中找到phase1/phase2，它是前面在分析组中定义的左旋/右旋圆偏振光相位。

    设置完成界面如下：

    运行扫参进程，注意要点击窗口内的运行按钮，不要点击顶部栏的运行按钮。

    运行完成后点击这个运行进程，默认在左下栏出现扫参结果。下图表明仿真结果符合PB相位理论。

     偏振转化率扫参进程的设置与相位扫参差别不大.

     下图是本文构建的超原子的偏振转化率(左)和原文(右)的对比.

三、超透镜仿真及优化

3.1 构建超透镜

    透射式聚焦超透镜将平面波前调制成球面波前。

     其相位分布公式为：

    假设超表面结构在一个二维平面上，将平面网格化。 根据PB相位理论，得到每个格点所需的旋转角度。

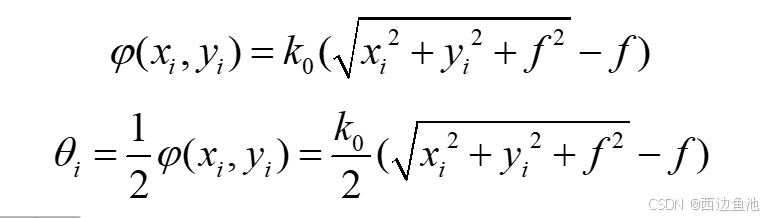
    使用Matlab计算得到“旋转角度-平面坐标”数据集合（当然也可以在lumerical FDTD中计算，不过lumerical的语法和matlab不太一样，需要另写脚本）。

%单位使用微米
clc;clear;
f=4;
D=10;
p=0.35;
lambda=0.7;
n=floor(D/p);
k=1;
for i=1:n
    for j=1:n
        x=-(n*p/2-p/2)+p*(j-1);
        y=-(n*p/2-p/2)+p*(i-1);
        s=sqrt(x^2+y^2);
        if s<=D/2
            Po(k,1)=x;Po(k,2)=y;
            Po(k,3)=180*(f-sqrt(x^2+y^2+f^2))/lambda;
            k=k+1;
           
        end
    end
end
[Po(k,1),Po(k,2)]=size(Po);
Po;
save("P70.mat","Po");

     上面这段代码定义了设计透镜的焦距f、直径D、网格周期p。最后需要生成一个.mat文件，该文件是旋转角度与坐标点对应的数据表。

selectall;
delete;
nm=1e-09;
um=1e-06;

hight=0.04*um;#金膜及刻蚀孔厚度
lambda=0.7e-6;#光源波长
L=0.215*um;
W=0.06*um;#刻蚀孔的长宽
p=0.35*um;#周期
D=10*um;#直径
matlabload("P70");
#基底
addrect;
set("name","substrate");
set("x",0);set("x span",10.5*um);
set("y",0);set("y span",10.5*um);
set("z max",0);set("z min",-0.1*um);
set("material","SiO2 (Glass) - Palik");
#金薄膜
addrect;
set("name","gold-layer");
set("x",0);set("x span",10.5*um);
set("y",0);set("y span",10.5*um);
set("z max",hight);set("z min",0);
set("material","Au (Gold) - Palik");
#添加刻蚀孔
addgroup;
set("name","structure");

m=640;#微结构数量
for (i=1:m){
addrect;#添加矩阵
name="etch"+num2str(i); 
set("name",name);#设置物体的名称
set("material","etch");#设置材料
set("render type","wireframe");#默认是细节渲染，也就是detailed
set("x",Po(i,1)*um);#设置x坐标，p矩阵第一列，单位微米
set("y",Po(i,2)*um);#设置y坐标，p矩阵第二列，单位微米
set("x span",L);
set("y span",W);
set("z min",0);
set("z max",hight);#尺寸设置
set("first axis","z");
set("rotation 1",Po(i,3));#旋转角设置
addtogroup("structure");
}
#添加光源
addplane;
set("name","Source_x");
set("injection axis","z");
set("direction","Backward");
set("plane wave type",1);
set("x",0);set("x span",11*um);
set("y",0);set("y span",11*um);
set("z",2*hight);
set("wavelength start",lambda);
set("wavelength stop",lambda);

addplane;
set("name","Source_y");
set("injection axis","z");
set("direction","Backward");
set("plane wave type",1);
set("polarization angle",90);set("phase",90);
set("x",0);set("x span",11*um);
set("y",0);set("y span",11*um);
set("z",2*hight);
set("wavelength start",lambda);
set("wavelength stop",lambda);

#在光源和结构之间添加光阑
x_span = D+0.5*um;   # x span of structure
y_span = D+0.5*um;   # y span of structure
R = D/2;      # 通光孔半径
x = R*cos(linspace(0,2*pi,80));
y = R*sin(linspace(0,2*pi,80));
V = [x,y;
     x_span/2,0;
     x_span/2,-y_span/2;
    -x_span/2,-y_span/2;
    -x_span/2, y_span/2;
     x_span/2, y_span/2;
     x_span/2,0];
add2dpoly;
set("name","aperture");
set("vertices",V);
set("x",0);set("y",0);set("z",-0.05*um);
set("material","PEC (Perfect Electrical Conductor)");
#仿真区域
addfdtd;
set("dimension",2); #1 = 2D, 2 = 3D
set("x",0);
set("x span",10.25*um);
set("y",0);
set("y span",10.25*um);
set("z max",0.1*um);
set("z min",-5*um);
set("mesh accuracy",2);
set("x min bc",1);  #这里用序号而不是Periodic的名称
set("y min bc",1);#1是PML边界；3是周期性边界
set("z min bc",1);
set("z max bc",1);



addpower;
set("x",0);set("x span",0.4*um);
set("y",0);set("y span",0.4*um);
set("z",-0.05*um);
set("name","T1");

addpower;
set("monitor type",5);
set("y",0);set("y span",10*um);
set("z max",0);set("z min",-5*um);
set("x",0);
set("name","T2");

    上面是构建超透镜结构的代码，新建一个空表的脚本新进去即可。 此脚本是构建整个透镜的脚本，与前面所述的与超原子有关的脚本不相干。

    此脚本包括光源(波长700纳米)、基底、基底上的超原子、仿真区域、光阑（因仿真区域为长方体，所以要加入一片圆形的通光孔）、监视器等。此脚本里面可以暂时不用添加监视器，待明确了要获取的数据后再手动添加也好。

    上图中的绿色区域即脚本中所指的“PEC” ，PEC是完美导体，起到屏蔽电磁场的作用。

3.2 超透镜仿真

    如果仿真区域包含光源,超透镜结构以及焦点所在的空间,这种方式可以称为直接仿真;如果仿真区域不包含焦点在内则称为间接仿真.间接仿真方法留在后面讨论，下面先介绍直接仿真。

1. 直接仿真

    光源沿着z轴的负方向入射,此时位于YZ平面(或者是XZ平面)上监视器能够记录焦点一侧空间中的光强分布(实际是电场强度的平方)。

clc;
clear;
E=getresult("T2","E");
x=getdata("T2","x");
y=getdata("T2","y");
z=getdata("T2","z");
f=getdata("T2","f");
E1=getattribute(E);
E2=E.E2;#|E|^2,前面的E2只是一个名称，是任意的，后面的E2是平方的意思，是固定用法
E3 = E.E;  # get all components in a single matrix. An extra dimension of length 3 will be added to the matrix, for each vector component.
E33=abs(E.Ex)^2+abs(E.Ey)^2+abs(E.Ez)^2;
E4=pinch(E2,4);
E4=pinch(E4,1);
E4=pinch(E4,1,length(y)/2);
plot(-z*1e6,E4,"z(um)","E^2");legend("z_line_plot");
po=findpeaks(E4);
zmax=-z(po)*1e6;

E5=pinch(E2,1);
E5=pinch(E5,3);#择去x和lambda
E5=pinch(E5,2,po);
plot(y*1e6,E5,"y(um)","E^2");legend("focal_plane_plot");
#计算半高宽
po2=findpeaks(E5);
top=E5(po2);
E5=-abs(E5-top/2);
plot(y*1e6,E5);
po3=findpeaks(E5,2);
FWHM=abs(y(po3(2))-y(po3(1)))*1e6;

    如果取z轴上光强最大处为实际焦点的位置, 那么实际焦距3.8微米与设计焦距4微米有一定差距。所以如果要获得焦平面的光强分布，还需要在实际焦点位置设置监视器进行二次仿真。

    直接仿真由于仿真区域大而占用了较大的内存，所需时间较多。二次仿真又使仿真时间增长一倍。而间接仿真可以有效地缩减所需内存和所用时间。

2. 间接仿真

    根据表面等效原理：如果一个给定的电磁结构，例如共振天线或者散射体，可以由一个具有一定的电流和磁流密度分布的等效封闭表面来代替。可以证明位于表面内的源向表面外辐射的场可以由表面上的场分量精确地确定。由于Maxwell方程是线性的，表面外的场可以通过计算表面上每个区域的远场投影，然后求和得到。

   间接仿真不仅能够节约仿真时间，还能在不重复仿真的情况下做任意空间位置的投影。在实际仿真的过程中，本文使用近场平面的电磁场信息做远场投影，这就要求该平面据结构足够近以接收更多的散射光。

    下面是间接仿真相关的一个脚本案例。其中“full_lens.fsp”是在直接仿真一节中构建的超透镜工程文件。在间接仿真的工程里面，不再需要在特定位置放置监视器（T1/T2），而需要在距离超表面结构不远处放置一个近场监视器T。下面这段代码主要是对函数farfieldexact3d的应用。

um=1e-6;

load("full_lens.fsp");
switchtolayout;

select("T1");
delete;
select("T2");
delete;
select("FDTD");
set("z min",-0.5*um);
addpower;
set("name","T");
set("x",0);set("x span",11*um);
set("y",0);set("y span",11*um);
set("z",-0.4*um);#基底的最底端是-0.1微米

#save("full_lens_farfield.fsp");

#load("full_lens_farfield.fsp");
if (haveresult("T")==false)
{
run;
}

#轴向方向上的远场投影
z=linspace(-0.1*um,-5*um,200);
x=0;y=0;
E_far=farfieldexact3d("T",x,y,z,{"field":"E and H"});
E2=E_far.E2;
E2=pinch(E2,4);
E2=pinch(E2);
plot(-z*1e6,E2,"z(um)","|E|^2");legend("E-z");
pos=findpeaks(E2);
z_f=z(pos);
#焦平面上的远场投影
x=linspace(-4*um,4*um,150);
y=linspace(-4*um,4*um,150);
E_far_focal=farfieldexact3d("T",x,y,z_f,{"field":"E and H"});
E3=E_far_focal.E2;
E3=pinch(E3,4);
E3=pinch(E3);
#visualize("E3");
image(x,y,E3,"x(um)","y(um)","|E|^2");
#电场强度分布曲线
E4=0.5*(pinch(E3,2,length(y)/2)+pinch(E3,2,length(y)/2+1));
plot(x*1e6,E4,"x(um)","|E|^2");legend("E-x");
E6=E4;
x6=x;
#计算半高宽
po2=findpeaks(E4);
top=E4(po2);
E4=-abs(E4-top/2);
#plot(y*1e6,E4);
po3=findpeaks(E4,2);
FWHM=abs(x(po3(2))-x(po3(1)))*1e6;

#YZ平面电场强度分布
y=linspace(-5*um,5*um,150);
z=-linspace(0*um,5*um,150);
x=0;
E_far_YZ=farfieldexact3d("T",x,y,z,{"field":"E and H"});
E5=E_far_YZ.E2;
E5=pinch(E5);
#plot(y,z,E5,"y(um)","z(um)","|E|^2");
image(y,z,E5,"y(um)","z(um)","|E|^2");

     下面对比直接仿真和间接仿真的结果是否一致。

直接仿真和间接仿真的对比。(a)(b)分别是直接仿真和间接仿真

在YZ平面上的光强分布；(c)沿Z轴的光强曲线

四、聚焦效率半高宽等参数的评估

     本文采用一种常用的定义来计算聚焦效率：在焦平面内，以焦斑中心为圆点，3倍半高宽为直径内的圆内的透过功率与透过光阑的总功率之比即为聚焦效率（此外还有一种基于艾里斑的定义）。

4.1 聚焦效率

     在运行过超透镜的仿真之后，首先投影出Z轴上光强并找出极值，该极值即为实际焦点。然后投影出焦点所在平面的场分布，积分计算透过功率。

um=1e-6;

load("full_lens.fsp");
switchtolayout;

#delete("T1");
select("T1");
delete;
select("T");
delete;
select("T2");
delete;
select("FDTD");
set("z min",-0.5*um);
addpower;
set("name","T");
set("x",0);set("x span",11*um);
set("y",0);set("y span",11*um);
set("z",-0.4*um);#基底的最底端是-0.1微米
setnamed("aperture","z",0.05*um);
addpower;
set("name","T1");
set("x",0);set("x span",11*um);
set("y",0);set("y span",11*um);
set("z",0.045*um);
save("full_lens_efficiency.fsp");

load("full_lens_efficiency.fsp");

if (haveresult("T")==false)
{
run;
}

#轴向方向上的远场投影
z=linspace(-0.1*um,-5*um,200);
x=0;y=0;
E_far=farfieldexact3d("T",x,y,z,{"field":"E and H"});
E2=E_far.E2;
E2=pinch(E2,4);
E2=pinch(E2);
plot(-z*1e6,E2,"z(um)","|E|^2");legend("E-z");
pos=findpeaks(E2);
z_f=z(pos);
#焦平面上的远场投影
x=linspace(-4*um,4*um,150);
y=linspace(-4*um,4*um,150);
E_far_focal=farfieldexact3d("T",x,y,z_f,{"field":"E and H"});
E3=E_far_focal.E2;
E3=pinch(E3,4);
E3=pinch(E3);
#visualize("E3");
image(x,y,E3,"x(um)","y(um)","|E|^2");
#电场强度分布曲线
E4=0.5*(pinch(E3,2,length(y)/2)+pinch(E3,2,length(y)/2+1));
plot(x*1e6,E4,"x(um)","|E|^2");legend("E-x");
#计算半高宽
po2=findpeaks(E4);
top=E4(po2);
E4=-abs(E4-top/2);
#plot(y*1e6,E4);
po3=findpeaks(E4,2);
FWHM=abs(x(po3(2))-x(po3(1)))*1e6;

#三倍半高宽区域内积分

f=E_far_focal.f;
pz=E_far_focal.Ex*conj(E_far_focal.Hy)-E_far_focal.Ey*conj(E_far_focal.Hx);
pz=pinch(pz);
pz=real(pz);
  x_center=0;	# integration range in m, set by user
  y_center=0;
  
  radius=1.5*FWHM*um;
  X=meshgridx(x,y);
  Y=meshgridy(x,y);
  filter = (radius)>=sqrt((X-x_center)^2+(Y-y_center)^2);
  T_filtered = 0.5* integrate(pz*filter,1:2,x,y);
  T1=getresult("T1","T");T1=T1.T;
T_filtered = T_filtered/sourcepower(f);
T_filtered=T_filtered/T1;
# Plot filter and transmission
image(x*1e9,y*1e9,filter,"x (nm)","y (nm)", " integration region");
#plot(f/1e12,T_filtered*100,"frequency (THz)","Power"," filter");

    上面这段代码与3.2-2中有共同片段。

    最终得到该超透镜的聚焦效率为36.76%。 在构建该超透镜的过程中，光阑被放在了金膜之后。实际上光阑放置在金膜之前（即光源与金膜之间）更为合理。所以，这个聚焦效率是偏高的。不过，即使是36.76%这个数值对于超透镜的聚焦效率来说也不算高。

4.2 半高宽

     根据弗朗禾费圆孔衍射理论，聚焦焦斑为一系列明暗相间的圆环，其光强分布为：

    其中m=(\pi Rsin\theta )/\lambda ，J_{_{1}}是一阶贝塞尔函数。设焦平面上一点到焦斑中心的距离为r，则有sin\theta =r/\sqrt{r^{2}+f^{2}}，绘制出r-I_{p}/I_{0}曲线，与归一化的焦斑垂切曲线对比。matlab中内置有贝塞尔函数。

%Ip=I0*J1(2m)^2/m^2,m=pi*R*sin()/lambda
%长度单位是微米
R=8;
f=6;
lambda=0.45;
%画离散的贝塞尔函数
z=-2:0.001:2;
for i=1:length(z)
    sin(i)=z(i)/sqrt(z(i)^2+f^2);
    m2(i)=2*pi*R/lambda*sin(i);
    J(i)=besselj(1,m2(i));
    m(i)=m2(i)/2;
    I(i)=J(i)^2/m(i)^2;
    x(i)=z(i);
end
plot(x,I);
hold on;
ylabel("归一化强度");
xlabel("Y(um)");

d=xlsread("聚焦光斑与夫朗和费衍射.xlsx",2);
d(:,1)=d(:,1)*1e6;
p=max(d(:,2));
d(:,2)=d(:,2)/p;
scatter(d(:,1),d(:,2),'.');
legend("衍射极限强度分布","仿真数据");

    (a)和(b)分别是直接仿真与间接仿真下的焦斑垂切与衍射极限曲线。而此时的衍射极限聚焦半高宽\Delta =\frac{\lambda }{2NA}=448nm（NA是数值孔径）。这说明该超透镜实现了接近衍射极限的聚焦行为。

五、写在后面

     这篇文章的开头提及了三种超透镜，但后两种目前不打算写了。这三种超透镜结构都很简单也很相似，掌握基本方法即可。

    不过后面的仿真其实也有问题：传播相位超透镜基本实现了偏振不敏感性，但聚焦焦斑不是圆形，而是在入射光偏振方向存在长轴的微椭圆；以及没有实现连续消色差超透镜等。

    初学者学习fdtd，一定好好利用官方资源。官方提供了丰富的脚本指令说明，简单案例等。一些资源门户）icon-default.png?t=O83Ahttps://innovationspace.ansys.com/forum/forums/topic/ansys-insight-lumerical-jishuziyuanjiqis-hiyongyaoqiu/

       一些官方案例：

     本文完结，欢迎讨论。

FDTD算法仿真超透镜，包括单元参数扫描和选择，聚焦建模设计
neDlJVl的博客
03-01 1974
在选择超透镜结构时，我们可以考虑不同的参数，如超透镜的厚度、曲率和材料选择。通过单元参数扫描和选择、聚焦建模设计、近场计算远场、相位计算及离散等步骤，我们可以实现对不同材料和波长的超透镜聚焦效果。通过对远场计算结果进行分析和处理，我们可以得到超透镜的远场信息，如聚焦光斑的形状和强度分布。通过监测仿真区域内的电磁场分布，我们可以获得超透镜的近场信息。FDTD算法仿真超透镜，包括单元参数扫描和选择，聚焦建模设计，近场计算远场，相位计算及离散，对不同材料 不同波长只需修改相关周期，高度等参数就可以实现聚焦。
基于Lumerical FDTD透射式聚焦超透镜仿真的简单案例（二）
qq_52317002的博客
11-03 2770
而且，我后面的工作也有一些没解决的问题：使用二氧化钛材料后聚焦效率获得显著提升，但是没有达到论文的水平（论文的在80%，我的不超过70%）；4.这里再多提一嘴，我是在个人电脑上运行的仿真，受算力所限，我的超透镜的尺寸都比较小，网格划分也会比较粗略。复现的Capasso文章的案例，超原子的尺寸和他用的一致，数值孔径也一致，但是我的透镜尺寸就要小的多。介绍了一种由金膜刻蚀矩形孔为基本单元构成的几何相位超透镜的仿真流程，有读者私信想要看复现Capasso课题组的那篇文献的几何相位超透镜仿真案例。
Metalens超构透镜设计：扫参分析、目标相位与半径计算及Lumerical FDTD与MATLAB的关联应用,出Metalens超构透镜lumerical fdtd仿真文件 本人研究生阶段从事的
02-09
Metalens超构透镜设计：扫参分析、目标相位与半径计算及Lumerical FDTD与MATLAB的关联应用,出Metalens超构透镜lumerical fdtd仿真文件。 本人研究生阶段从事的是超构透镜设计，可1如何扫参得到相位和半径的关系可2目标相位和目标半径计算代码(传输相位，几何相位型均有) 3.Lumeical fdtd和MATLAB关联设计一键建模和运行有关超透镜，超构透镜和lumerical fdtd的 ,Metalens超构透镜; Lumerical FDTD仿真; 扫参方法; 相位与半径关系; 目标相位和目标半径计算代码; MATLAB关联设计; 一键建模和运行; 超透镜设计。,研究生超构透镜设计研究：仿真参数扫描与代码求解以及Lumerical FDTD与MATLAB的一键建模与运行。
FDTD模拟教程
06-09
是讲述FDTD的详细教程，可以对光场分布进行模拟，是很不错的学习资料
多波长 独立聚焦超构透镜 fdtd仿真 超表面 复现论文：2017年OE：Dispersion controlling meta-lens at
最新发布
AwGaVKXvuUPs的博客
03-06 469
论文介绍：单元结构为硅矩形纳米柱结构，通过调节结构的长宽尺寸，可以找到三个波长处高偏振转换效率的参数，通过调整纳米柱的转角实现连续的几何相位调节，构建具有三个独立波长聚焦相位分布的超构透镜模型，可实现可见光波段的三原色聚焦和成像；最后，我们根据设计的超构透镜模型和进行仿真所得的结果，复现了实际的聚焦效果。案例内容：主要包括硅纳米柱的单元结构仿真、偏振转换效率的计算，几何相位的计算，超构透镜的不同色散曲线对应的超构透镜相位计算matlab代码，不同色散的超构透镜模型以及对应的远场电场分布计算；
基于几何相位设计的超构透镜：从可见光到任意波段的聚焦与成像技术,基于几何相位设计的超构透镜：从可见光到任意波段的聚焦与成像技术,几何相位超构透镜，圆偏振聚焦，超表面 复现：2016年Science ：
03-03
基于几何相位设计的超构透镜：从可见光到任意波段的聚焦与成像技术,基于几何相位设计的超构透镜：从可见光到任意波段的聚焦与成像技术,几何相位超构透镜，圆偏振聚焦，超表面 复现：2016年Science ：Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging 介绍：二氧化钛纳米柱由几何相位设计，实现接近衍射极限的超构透镜模型，用于可见光波段聚焦和成像； 案例内容：主要包括二氧化钛纳米柱的单元结构仿真、几何相位计算，超构透镜的双曲相位计算代码以及可见光波段405nm 532nm和633nm三个波长的超构透镜模型，和对应的远场电场分布计算以及聚焦效率计算； 案例包括fdtd模型、fdtd设计脚本、Matlab计算代码和复现结果，以及一份word教程，超构透镜的相位计算代码和几何相位与结构的匹配代码可用于任意波段的超构透镜，具备可拓展性。 ,几何相位; 复现研究; 超构透镜; 纳米柱单元; 双曲相位计算代码; 远场电场分布; 聚焦效率计算; 几何相位
Lumerical官方案例、FDTD时域有限差分法仿真学习（十四）——超透镜（Metalens）
热门推荐
weixin_45719141的博客
07-08 2万+
这个例子的目的是设计一个由圆柱形纳米棒组成的衍射超透镜。 纳米棒的半径和排列经过调整以在超透镜表面上产生所需的相位分布。 该设计通过近场和远场分析在 Ansys FDTD、RCWA（严格耦合波分析）和 OpticStudio 中得到验证。...
FDTD应用入门与实例
01-13
英文版的FDTD solution的入门以及实例的介绍
Lumerical官方案例、FDTD时域有限差分法仿真学习（二）——宽带光栅耦合器(Broadband grating coupler (2D))
weixin_45719141的博客
03-03 1万+
这个 2D FDTD 示例展示了如何获得光栅耦合器的宽带特性，并将结果与实验数据进行比较。
Lumerical官方案例、FDTD时域有限差分法仿真学习（十）——光栅耦合器（Grating coupler）
weixin_45719141的博客
04-02 1万+
设计一个光栅耦合器，将光子芯片表面的单模光纤连接到集成波导。 内置粒子群优化工具用于最大化耦合效率，并使用组件 S 参数创建 INTERCONNECT 中的紧凑模型。 它还展示了如何使用 CML 编译器提取这些参数以生成紧凑模型。
FDTD仿真实例直播合集
YHJX57的博客
09-06 1247
2022年10月22日-10月23日 在线直播 2022年10月29日-10月30日 在线直播
超透镜.rar_FDTD 超透镜_FDTD 透镜_FOCUSING _fdtd_超透镜
07-14
Metalenses at visible wavelengths:Diffraction-limited focusing and subwavelength resolution imaging使用FDTD仿真脚本文件
FDTD经典教程
06-04
比较全面的关于FDTD算法的介绍。欢迎下载。主要用于电磁计算方面。
基于FDTD方法模拟一维电磁波在超材料的传播（Matlab）
05-14
用FDTD方法，使用Matlab模拟电磁波从自由介质传入到超材料（左手材料）的代码，在一维中。
微环谐振器，r=10um，fdtd仿真
04-23
lumerical fdfd仿真文件，r=10um，适合初步仿真的例子,运行完文件太大上传不了，自己运行一下
metalens.rar_FDTD超透镜_metalens_metalens FDTD_超透镜_透镜
07-15
在FDTD solutions 绘制超透镜
关于有限时域差分法，Lumerical-FDTD Solutions的中文指导手册
09-02
《关于有限时域差分法，Lumerical-FDTD Solutions的中文指导手册》是一份详尽的教程，针对光学建模仿真领域的初学者和专业人士。该手册覆盖了Lumerical公司的FDTD Solutions软件的各个方面，从基本界面介绍到高级...
Ansys Lumerical | 超透镜设计第三部分：如何基于Lumerical以及OpticStudio完成全面的超透镜设计
ueotek的博客
10-22 1576
在前两部分的文章中，我们主要讨论了如何在 Lumerical 中定义目标相位的分布，并将该解析解用于 OpticStudio 中设计理想的相位掩膜，并且后续可以使用 FDTD 或者 RCWA 算法对其进行扫描仿真。在这一步中，我们扫描纳米棒的高度和半径，并获得其透射、相位和近场信息，从而选择出对应所需传输和相位特性的纳米棒高度情况，然后保存相位与光场相对于半径的结果以供后续步骤使用。本案例的目的是设计一个由圆柱形纳米棒组成的衍射超透镜，人为调整纳米棒的半径和排列可以在超透镜表面上产生所需的相位分布。
fdtd超表面仿真案例
12-29
### FDTD 方法用于超表面仿真的案例 #### 使用 Lumerical FDTD 对超透镜进行建模 当涉及到超透镜的设计与仿真时，Lumerical 提供了一个详细的实例来展示如何利用已知的半径分布创建并优化这些结构。这种方法虽然...
评论 160
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值