数学——图形题

1：计算不同区域面积

在图中，有一个正方形ABCD，其中，AB=BC=CD=DA=a。以四个顶点A, B, C, D为圆心，以a为半径，画四个圆弧：以A为圆心的圆弧，从相邻顶点B开始，到相邻顶点D结束；所有其他的圆弧都以类似的方式画出。如图所示，以这种方式在正方形中画出了三种不同形状的区域，每种区域用不同阴影表示。请您计算不同阴影部分的总面积。
在图中，有一个正方形ABCD，其中，AB=BC=CD=DA=a。以四个顶点A, B, C, D为圆心，以a为半径，画四个圆弧：以A为圆心的圆弧，从相邻顶点B开始，到相邻顶点D结束；所有其他的圆弧都以类似的方式画出。如图所示，以这种方式在正方形中画出了三种不同形状的区域，每种区域用不同阴影表示。请您计算不同阴影部分的总面积。

输入格式:
输入的每一行都给出一个浮点数a（0<=a<=10000），表示正方形的边的长度。输入以EOF结束。

输出格式:
对于每一行的输入，输出一行，给出三种不同阴影部分的总面积：给出三个保留小数点后三位的浮点数，第一个数字表示条纹区域的总面积，第二个数字表示点星罗棋布的区域的总面积，第三个数字表示其余区域的面积。

输入样例:
0.1
0.2
0.3
输出样例:
0.003 0.005 0.002
0.013 0.020 0.007
0.028 0.046 0.016

输入格式:
输入的每一行都给出一个浮点数a（0<=a<=10000），表示正方形的边的长度。输入以EOF结束。

输出格式:
对于每一行的输入，输出一行，给出三种不同阴影部分的总面积：给出三个保留小数点后三位的浮点数，第一个数字表示条纹区域的总面积，第二个数字表示点星罗棋布的区域的总面积，第三个数字表示其余区域的面积。

输入样例:

0.1
0.2
0.3

输出样例:

0.003 0.005 0.002
0.013 0.020 0.007
0.028 0.046 0.016

![在这里插入图片描述](https://img-blog.csdnimg.cn/7b4b0b4c6b924894bbf53194103f98c2.png
题目解析：如图所示把所求分别连接AE，BE，然后作三角形ABE的垂线EO，由题意可知AE，BE，AB分别为各自所在圆的半径，所以有AE=BE=AB=a，由图形可以得出x + y == S_扇形DEA - （S_扇形BEA - S_三角形AEB）
==> x + y == (1 / 3)_S扇形ADB - ((2 / 3)S_扇形ADB - S_三角形AEB)
==> x + y == sqrt(3) / 4 a² - pi / 12 a² - - - - - - (1)
由图可得：
4 * x + 4 * y + z == a² - - - - - - (2)
2x + 3y + z == (1 / 4) pi a² - - - - - - (3)
化简求阴影得：
4x == a²(4 - sqrt(3) - (2/ 3) pi)
4y == a²(2sqrt(3) - 4 + pi / 3)
z = a²(1 - sqrt(3) + pi / 3)

#include <iostream>
#include <cmath>

#define pi 3.1415926535

using namespace std;

int main()
{
    double a;
    while (cin >> a)
        printf("%.3f %.3f %.3f\n", 
               a * a * (1 - sqrt(3) + pi / 3),
               a * a * (2 * sqrt(3) - 4 + pi / 3),
               a * a * (4 - sqrt(3) - 2 * pi / 3));
    return 0;
}

2：我是送分题

大家最喜欢的送分题他来了，现在有一个等式F(n) = F(n - 1) + 2 * F(n - 2) + 3 * F(n - 3)，F(1) = 1, F(2) = 2,F(3) = 3,
现在给出一个n请你求出F(n)对1e9+ 7取模.看到这里你是不是想大喊一声芜湖，起飞，老送分题咯。

输入格式:
简简单单一个n(4 <= n <= 1e9)

输出格式:
输出F(n)对1e9+ 7取模

输入样例:
在这里给出一组输入。例如：

4

输出样例:
在这里给出相应的输出。例如：

10

代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB

解析：首先从时间考虑，这题数据范围在4 ~ 1e9 O(N)肯定是过不去的，所以我们需要考虑log(N)的做法（快速幂和最大公约数），这题显然可以看出和最大公约数没关系，所以我们从快速幂入手，由题意可知，我们需要根据递推式求出如下的目标矩阵

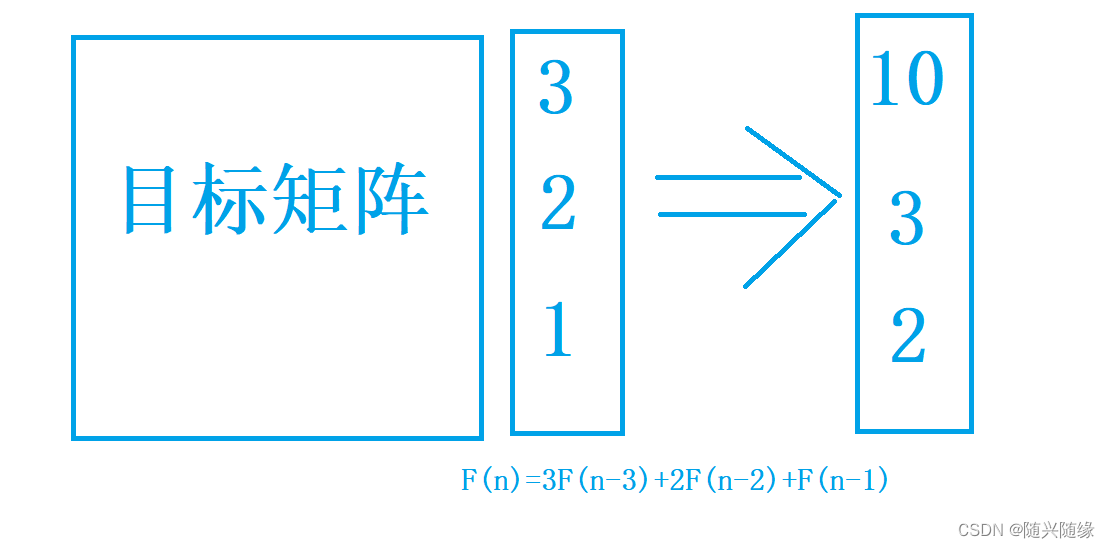
可以推出如下结果：

当n>3时推出如下公式

#include <iostream>
#include <cstring>

using namespace std;

const int mod = 1e9 + 7;

typedef long long LL;

struct Mx
{
    LL g[3][3];
    Mx()
    {
        memset(g, 0, sizeof g);
    }
};

Mx mul(Mx a, Mx b) //  矩阵乘法
{
    Mx res;
    for (int i = 0; i < 3; i ++ )
        for (int j = 0; j < 3; j ++ )
        {
            LL sum = 0;
            for (int k = 0; k < 3; k ++ )
                sum = (sum + a.g[i][k] * b.g[k][j]) % mod;
            res.g[i][j] = sum;
        }
    return res;
}

Mx Mx_pow(Mx a, LL b) //  矩阵快速幂
{
    Mx res;
    //  构造单位矩阵
    res.g[0][0] = res.g[1][1] = res.g[2][2] = 1;
    
    while (b)
    {
        if(b & 1) res = mul(res, a);
        a = mul(a, a);
        b >>= 1;
    }
    return res;
}

int main()
{
    LL n;
    Mx a;
    
    cin >> n;
    
    //  目标矩阵
    a.g[0][0] = a.g[1][0] = a.g[2][1] = 1;
    a.g[0][1] = 2;
    a.g[0][2] = 3;
    
    a = Mx_pow(a, n - 3);
    
    LL ans[3][1], num[3][1];
    num[0][0] = 3, num[1][0] = 2, num[2][0] = 1;
    
    for (int i = 0; i < 3; i ++ )
    {
        LL sum = 0;
        for (int j = 0; j < 3; j ++ )
            sum = (sum + a.g[i][j] * num[j][0]) % mod;
        ans[i][0] = sum;
    }
    cout << ans[0][0];
    
    return 0;
}