代码说明
- 导入库和数据x,y:必须都是数组或者列表,否则会报错

import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
import pandas as pd
from math import e
fp=pd.read_excel('人口.xlsx')
Xi = np.linspace(0,68,69)
Yi = fp["实际总人口数/亿"].values
这里提一下列表和数组如何转换,如果报Xi和Yi的错,就是这个问题。
列表->数组:np.array()
数组->列表:np.tolist()
- 目标函数:参数中放入参数和变量x,值得注意的是变量必须从零开始,不然会出错,图会不匹配。(应该和原理有关系,会消除偏移量的影响)
def func(p,x):
a,b,c=p
return (a-2.0*b)*(5.5196-b)/(5.5196-b+(a-b-5.5196)*e**(-c*x))+b #此处记得自然底数需要引入math库,否则会报错
- 残差函数:为了使用差值判断拟合程度
def error(p,x,y):
return func(p,x)-y #x、y都是数组(列表),故返回值也是个数组(列表)
- 给定参数的初始值:有几个参数就给几个初始值,这个初始值是拟合时候使用的。随便给,影响不大。
p0=[18.0571,3.4704,0.0603]
- 主函数:leastsq函数是黑箱操作,按要求写参数就行,返回Para[0]是未知参数,Para[1]是状态,1-4表示拟合成功
Para=leastsq(error,p0,args=(Xi,Yi)) #把error函数中除了p以外的参数打包到args中
a,b,c=Para[0]
print("a=",a,"b=",b,"c=",c)
- 画图:
plt.figure(figsize=(8,6))#设置画布大小
plt.scatter(Xi,Yi,color="b",label="Sample Point",linewidth=1) #画样本点
x=np.linspace(0,101,1000)
y=(a-2.0*b)*(5.5196-b)/(5.5196-b+(a-b-5.5196)*e**(-c*x))+b
plt.xticks(range(1949,2020,5))
plt.plot(x,y,color="r",label="Fitting Line",linewidth=2) #画拟合直线
plt.legend()
plt.show()
print((a-2.0*b)*(5.5196-b)/(5.5196-b+(a-b-5.5196)*e**(-c*2050))+b)
完整代码
###最小二乘法试验###
import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
import pandas as pd
from math import e
###采样点(Xi,Yi)###
fp=pd.read_excel('人口.xlsx')
Xi = np.linspace(0,68,69)
Yi = fp["实际总人口数/亿"].values
###需要拟合的函数func及误差error###
def func(p,x):
a,b,c=p
return (a-2.0*b)*(5.5196-b)/(5.5196-b+(a-b-5.5196)*e**(-c*x))+b
def error(p,x,y):
return func(p,x)-y #x、y都是列表,故返回值也是个列表
#TEST
p0 = [18.0571,3.4708,0.0603]
#print( error(p0,Xi,Yi) )
###主函数从此开始###
Para=leastsq(error,p0,args=(Xi,Yi)) #把error函数中除了p以外的参数打包到args中
a,b,c=Para[0]
print("a=",a,"b=",b,"c=",c)
###绘图,看拟合效果###
plt.figure(figsize=(8,6))
plt.scatter(Xi,Yi,color="b",label="Sample Point",linewidth=1) #画样本点
x=np.linspace(0,101,1000)
y=(a-2.0*b)*(5.5196-b)/(5.5196-b+(a-b-5.5196)*e**(-c*x))+b
plt.xticks(range(1949,2020,5))
plt.plot(x,y,color="r",label="Fitting Line",linewidth=2) #画拟合直线
plt.legend()
plt.show()
print((a-2.0*b)*(5.5196-b)/(5.5196-b+(a-b-5.5196)*e**(-c*2050))+b)
实例
2050年人口预测
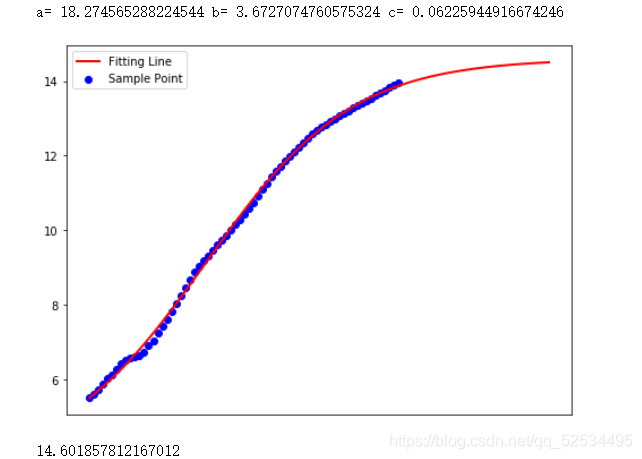








 该代码实例展示了如何运用最小二乘法(leastsq函数)对人口增长数据进行拟合。首先,从Excel文件中读取人口数据,然后定义目标函数和残差函数。通过leastsq函数找到最佳参数,实现对数据的曲线拟合。最后,绘制样本点和拟合曲线,预测2050年的人口数量。
该代码实例展示了如何运用最小二乘法(leastsq函数)对人口增长数据进行拟合。首先,从Excel文件中读取人口数据,然后定义目标函数和残差函数。通过leastsq函数找到最佳参数,实现对数据的曲线拟合。最后,绘制样本点和拟合曲线,预测2050年的人口数量。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








