第二型线面积分（习题部分）

目录​​​​​​​

第一型曲线积分

第二型曲线积分

第二型曲面积分

---

• 第一型曲线积分

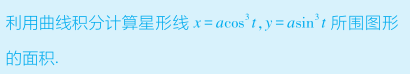
用二型积分的知识求面积，想到格林公式，从右往左用，将表示面积的二重积分转化为第二型曲线积分即可。

所以我们选取 ,正向为积分路径C，选取被积表达式中的Q=x, P=-y即可，由格林公式得

 

                ​​​​​​​        ​​​​​​​        ​​​​​​​         

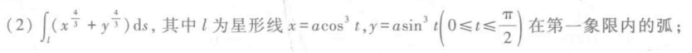
 分析：

这两道题目都有一个共同点技巧，就是巧妙地利用已知的积分曲线方程，去简化被积表达式。

第一个题，给出的圆周方程与被积表达式存在代数恒等关系，可以利用平方将被积表达式转化为只含有a的常数式子，提到积分号外部，计算的其实就是空间圆周的周长。

计算周长，需要圆的半径，此时用立体几何知识，求出圆心到平面的距离，勾股定理求出来。

解：

第二个题，由于曲线方程具有对等性，x、y、z三者地位相同，就向着平方和的形式转化。 

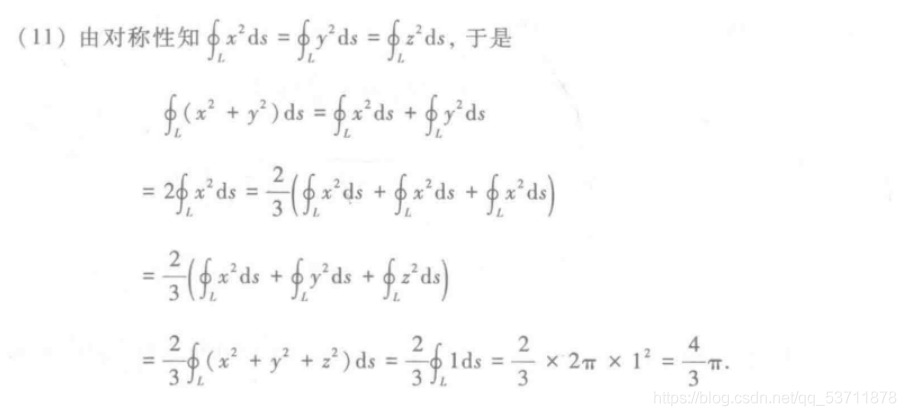
• 第二型曲线积分

 

去年考题，比较基础 

首先计算偏导数之差

 虽然不简洁，但是注意这个结果是转化后的二重积分的被积表达式，利用对称性知道这个结果为零，因此考虑使用格林公式。

 

利用两者关系，关键是求出正确的方向向量的方向余弦。方向向量的方向要与曲线的方向一致。

• 第二型曲面积分

画出大致图形，利用高斯公式。 

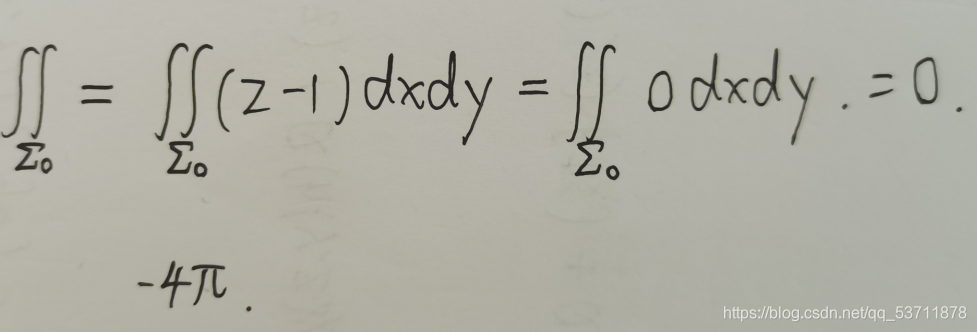
 首先需要求出曲面方程，注意技巧，需要记忆公式，绕着哪个轴旋转，哪个轴对应的变量就不变，用另外两个变量的平方和的平方根代替另一个变量。

 剩下的就是利用高斯公式了。