一些习题,补充说明本章的考点,并复习本章的主要内容。
习题的主要考点:
阿贝尔引理与收敛半径的求法
1.


这两道题思路完全一致,首先需要明白条件收敛的概念,然后结合阿贝尔引理来得出收敛域。

2.

为方便使用阿贝尔引理,我们先作换元,将x+1换成t,即幂级数的标准形式,随即使用阿贝尔引理:

我们可以知道收敛半径一定大于等于4。假设R大于4,由阿贝尔引理,当-R< x < R时,幂级数是绝对收敛的,与此处矛盾,所以收敛半径R=4。
3.

给出的是一个数项级数的敛散性,但是可以将-2抽象成变量x,它就变成了一个幂级数;
-2处幂级数是收敛的,因此当-2 < x < 2时,幂级数绝对收敛;
当x=1时,幂级数也收敛。
4.


根据已知的幂级数的收敛半径,待求幂级数只是作了一个换元而已(比如第一题是用代换了x,因此可以很方便地解不等式得到结果。

幂级数展开式的求法
5.

此题无非就是一个逐项微分的问题,其他的套用公式运算即可。

接下来就可以逐项微分了:
时刻注意下标问题(一般是不会出现负数的,届时需要调整)。
最后一步需要求一次收敛域,写出最终结果。

6.

可以分子分母同时乘以x^2-1,实现一连串的处理:

7.


8.
![]()

最后的形式都应该是(x-5)的幂的和的形式(非标准形式的幂级数),所以我们最好换一个元,令x-5 = t,将新的函数在t=0处展开为幂级数(可以直接套用公式),最后再换回来。处理方法会用到因式分解与裂项。

(关于系数的得来,根据待定系数法)
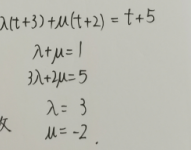
最后还需要求收敛域

幂级数的求和

9.
求幂级数的和函数:

此题要用到的公式是公式六,有分母,所以需要逐项积分,并且分母中有二次,积分也相应地需要积分两次。
可以先在草稿纸上演算一番:

然后得到了这样一个代换式后,就可以开始求和了。
当然第一步求收敛域:

第二步,求和函数(积分与求和换序):
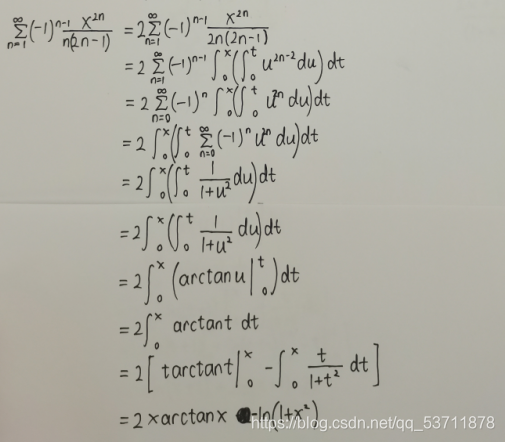
思考过程也可以先求出求二阶导后的级数的和函数,再对和函数求两次积分。
10.


11.
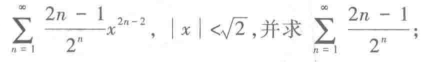
要求一个具体的数项级数,首先需要求出一般情况下的函数项级数(幂级数)的和函数,将变量换成1代入和函数,就可以得到结果。


傅里叶级数与收敛定理
12.

这题主要就是考查狄利克雷条件,根据这个定理就可以求出结果,无需计算傅里叶级数的系数。

13.
![]()

解

判断级数敛散性与相关性质
14.
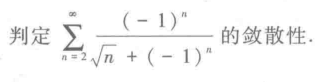

15、


16、

选B,用比值法判断出原级数不绝对收敛,故原级数发散。
17、



























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










