《机器翻译：基础与模型》笔记：统计机器翻译（三）（基于词的机器翻译建模）_用于把单词区分开来。而它的输出结果是一个概率,表示在给定输入的情况下,最可能返-CSDN博客

本文链接：https://blog.csdn.net/qq_53769632/article/details/147463634

文章目录

前言
基于词的机器翻译
参考文献
写在文末

前言

本期将进行深入统计机器翻译，详细介绍基于词的机器翻译建模以及介绍噪声信道模型与IBM模型1，介绍其建模，训练，解码的过程。

基于词的机器翻译

在翻译一个句子的时候，我们可以把其中的每个单词翻译成对应的目标语言单词，然后调整目标语言单词的语序，最后得到整句句子。我们把这个过程总结为三个步骤，分析转化生成。

分析：将源语言句子表示为适合机器翻译的结构。在基于词的翻译模型中，处理单元是单词，因此在这里也可以简单地将分析理解为分词。
转换：把源语言句子中的每个单词翻译成目标语言单词。
生成：基于转换的结果，将目标语译文变成通顺且合乎语法的句子。
但是如何通过机器实现这一个过程，就是我们需要解决的，这个思路被称为基于词的机器翻译。同时这个过程包括基于单词的转化、句子的转化以及词序的调整，我们先从单词级翻译模型进行介绍，再介绍基于句子的翻译模型还有n-gram语言模型保证词序。

单词级翻译模型

单词翻译概率

单词翻译概率描述的是一个源语言单词与目标语言译文构成正确翻译的可能性。以汉译英为例，当翻译“我”这个单词时，可能直接会想到用“I”、“me”或“I’m”作为它的译文。不同的词有不同的概率，像“you”等词在翻译我的时候会获得很低的概率。然而如何得到这个概率呢，让我们接着往下看。
在这里插入图片描述

如何学习单词翻译概率

我们还是可以采用基于频次的方法，令X和Y分别表示源语言和目标语言的词汇表。对于任意源语言单词x∈X，所有的目标语单词y∈Y 都可能是它的译文。给定一个互译的句对(s,t)，可以把P(x↔y;s,t) 定义为：在观测到(s,t)的前提下x和y互译的概率。其中x是属于句子s中的词，而y是属于句子t中的词。P(x↔y;s,t)的计算公式描述如下：
在这里插入图片描述
如果有更多的句子，假设有K个互译句对，仍然使用基于相对频次的方法估计翻译概率P(x,y)，只需对其进行求和即可：

在小规模数据上，翻译现象可能不明显，但当使用的数据量增加到一定程度，翻译的规律会很明显的体现出来。

句子级翻译模型

有了单词级翻译模型不够，最重要的还是需要句子级翻译模型，能把一句话翻译为另一句话，即对应源语言s和目标语言t，计算P(t|s)。由于无法像单词级翻译模型那要进行计数统计，这里我们引入一个函数g(s,t)来表示P(t|s)。给定s，翻译结果t出现的可能性越大，g(s,t)的值越大；t出现的可能性越小，g(s,t)的值越小。换句话说，g(s,t)和翻译概率P(t|s)呈正相关。
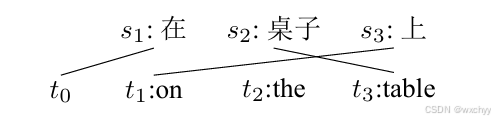
在这里插入图片描述
分母对于函数g(s,t)在做归一化，使相加之和为1。但现在如何对g(s,t)进行设计和计算，我们引入一个重要概念，词对齐。词对齐描述了平行句对单词之间的对应关系。**本质上句子的对应是由单词之间的对应所表示的。**通过单词概率的对应关系，我们表示句子对应的对应关系。看一个具体的实例：
在这里插入图片描述
我们可以把这些词对齐连接构成的集合作为词对齐的一种表示，记为A，即A={(1,1),(2,4),(3,5),(4,2),(5,3)}。对于句对(s,t)，假设可以得到最优词对齐A^，于是可以用上述我们介绍的单词翻译概率来计算g(s,t)：

现在我们就通过单词级翻译模型构建了句子级翻译模型。
在这里插入图片描述
不过它有一个重要的问题，我们没有考虑词序，源语言句子“我对你感到满意”有两个翻译结果，第一个翻译结果是“I am satisfied with you”，第二个是“I with you am satisfied”。它们的g(s,t)是一致的，然而词序却有明显差异。这里我们通过第一期博客介绍的n-gram模型，它也是统计机器翻译中确保流畅翻译结果的重要手段之一，以2-gram 语言模型为例，可以使用如下公式计算一个词串的概率：
在这里插入图片描述
由此，我们得到新的g(s,t),不仅考虑了翻译的准确性，同时考虑了流畅度。

解码

有了句子级翻译模型，我们就能对新输入的句子生成最佳译文，这个过程被称为解码。
在这里插入图片描述
然而如何找到argmax以实现找到最佳译文是解码的任务，如果去枚举整个搜索空间，它的复杂度是指数级别的，是NP问题。这里我们使用一种贪心的搜索方法以实现机器翻译的解码，他把解码分为若干个步骤，每步只翻译一个单词，并保留当前最好的结果，直至所有原语言单词都被翻译完毕。
在这里插入图片描述

该算法的核心在于，系统一直维护一个当前最好的结果，之后每一步考虑扩展这个结果的所有可能，并计算模型得分，然后再保留扩展后的最好结果。注意，在每一步中，只有排名第一的结果才会被保留，其他结果都会被丢弃。这也体现了贪婪的思想。
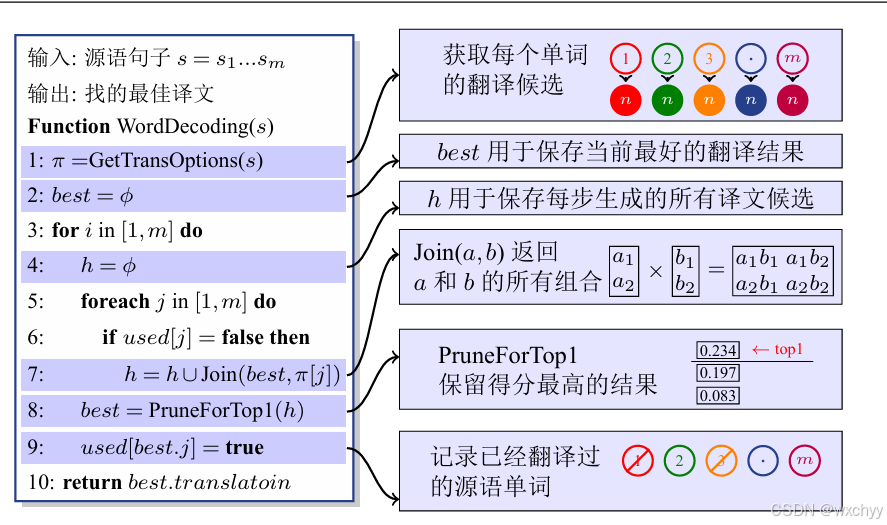
在这里插入图片描述

噪声信道模型

之前介绍了一个简单的基于词的统计机器翻译模型，不过如何用更严密的数学模型进行描述呢。这里引入了IBM模型，而IBM模型又是基于噪声信道模型。它是由Shannon在上世纪40年代末提出来的，并于上世纪80年代应用在语言识别领域，后来又被Brown等人用于统计机器翻译中。
在噪声信道模型中，目标语言句子t（信源）被看作是由源语言句子s（信宿）经过一个有噪声的信道得到的。如果知道了s和信道的性质，可以通过P(t|s)得到信源的信息。
在这里插入图片描述
举个例子，对于汉译英的翻译任务，英语句子t可以被看作是汉语句子s加入噪声通过信道后得到的结果。换句话说，汉语句子经过噪声信道传输时发生了变化，在信道的输出端呈现为英语句子。于是需要根据观察到的汉语特征，通过概率P(t|s)猜测最为可能的英语句子。这个找到最可能的目标语句（信源）的过程也被称为解码（Decoding）。直到今天，解码这个概念也被广泛地使用在机器翻译及相关任务中。这个过程也可以表述为：给定输入s，找到最可能的输出t，使得P(t|s)达到最大：
在这里插入图片描述
在IBM模型中，可以使用贝叶斯准则对P(t|s) 进行如下变换：
包括三个部分：

第一部分是由译文t到源语言句子s的翻译概率P(s|t)，也被称为翻译模型。它表示给定目标语句t生成源语句s的概率。需要注意是翻译的方向已经从P(t|s) 转向了P(s|t)，但无须刻意地区分，可以简单地理解为翻译模型描述了s 和t的翻译对应程度；
第二部分是P(t)，也被称为语言模型。它表示的是目标语言句子t出现的可能性
第三部分是P(s)，表示源语言句子s出现的可能性。因为s是输入的不变量，而且P(s)>0，所以省略分母部分P(s)不会影响 P(s|t)P(t)/ P(s)最大值的求解。
接下来我们具体看一下IBM模型如何对我们之前的基于词的机器翻译进行描述，训练，以及解码。

统计机器翻译的三个基本问题

现在我们简单总结一下统计机器翻译，为了实现这个过程，我们需要三个流程：

建模：如何建立P(s|t)和P(t)的数学模型，换句话说，就是用可计算的方式对翻译问题和语言建模问题进行描述。
训练：如何获得P(s|t)和P(t)所需的参数。如何从数据中得到模型的最优参数。
解码：如何完成搜索最优解的过程，也就是求argmax。
接下来我将通过IBM模型对这个流程进行详细的介绍。

1 IBM模型的一个基本的假设就是词对齐假设，词对齐描述的词对齐给我们之前介绍的词对齐有一些区别。

一个源语言单词只能对应一个目标语言单词。但是却没对目标语言单词进行约束，我们称之为非对称的词对齐。
源语言单词可以翻译为空，这是它对应一个虚拟或者伪造的目标语单词 $t_0$ 上。我们称之为空对齐。

2 IBM模型假设：句子之间对对于可以由单词之间的对应进行表示，由此翻译句子的概率被转化为词对齐生成的概率。这里我们将词对齐a看成翻译的隐变量。通过访问s和t之间所有可能的词对齐a，并把对应的对齐概率进行求和，得到了t到s的翻译概率。

在这里插入图片描述
举个实际求解的例子：

然而隐含变量a仍然很复杂，在IBM模型中，进一步对其进行分解，使用链式法则：

简单来说，当求P(s,a|t)时，首先根据译文t确定源语言句子s的长度m；当知道源语言句子有多少个单词后，循环m次，依次生成第1个到第m个源语言单词；当生成第j个源语言单词时，要先确定它是由哪个目标语译文单词生成的，即确定生成的源语言单词对应的译文单词的位置；当知道了目标语译文单词的位置，就能确定第j个位置的源语言单词。

我们用实例来解释一下：例子中，源语言句子“在桌子上”目标语译文“onthetable”之间的词对齐为a={10,23,31}。计算过程如下：

首先根据译文确定源文s的单词数量（m=3），即P(m=3|“t0 on the table”)；
再确定源语言单词s1由谁生成的且生成的是什么。可以看到s1由第0个目标语单词生成，也就是t0，表示为P(a1 =0 |ϕ,ϕ,3,“t0onthetable”)，其中ϕ表示空。当知道了s1是由t0生成的，就可以通过t0生成源语言第一个单词“在”，即P(s1 =“在”|{1−0},ϕ,3,“t0 on the table”)
类似于生成s1，依次确定源语言单词s2和s3由谁生成且生成的是什么；
最后得到基于词对齐a的翻译概率为：

IBM模型1

但是上述公式这其中还是有两个问题。

首先，求P(s,a|t)要求对所有的词对齐概率进行求和，但是词对齐的数量随着句子长度是呈指数增长，如何遍历所有的对齐a。
其次，虽然对词对齐的问题进行了描述，但是模型中的很多参数仍然很复杂。
为此提出了IBM模型1、IBM模型2、IBM模型3、IBM模型4以及IBM模型5。本期介绍较为简单的IBM模型1。
假设P(m|t)为常数ε，即源语言句子长度的生成概率服从均匀分布，如下：
对齐概率仅依赖于译文长度l，即每个词对齐连接的生成概率也服从均匀分布。对于任意源语言位置j对齐到目标语言任意位置都是等概率的。
源语单词sj 的生成概率仅依赖与其对齐的译文单词

最终得到P(s|t)的表达式：

解码

如果模型参数给定，可以使用IBM模型1对新的句子进行翻译。可以使用之前介绍的贪婪搜索算法，对齐进行计算每个译文候选的IBM模型翻译概率。

训练

在完成了建模和解码的基础上，剩下的问题是如何得到模型的参数。这也是整个统计机器翻译里最重要的内容。统计机器翻译模型的训练是一个典型的优化问题。简单来说，训练是指在给定数据集（训练集）上调整参数使得目标函数的值达到最大（或最小），此时得到的参数被称为是该模型在该目标函数下的最优解。
在这里插入图片描述
我们将其写成数学形式。

回到IBM模型的优化问题上。以IBM模型1为例，优化的目标是最大化翻译概率P(s|t)。

我们可以对其使用拉格朗日乘数法将其转化为无约束问题。

对其求导计算以及待入：

最后使用期望最大化算法(EM)对其进行迭代计算，使其最终收敛到最优值。通过EM算法进行实现。算法最终的形式并不复杂，因为只需要遍历每个句对，之后计算f(·|·)的期望频次，最后估计新的f(·|·)，这个过程迭代直至f(·|·)收敛至稳定状态。
在这里插入图片描述
至此，IBM模型1的训练也介绍完了。