强化学习:TRPO,PPO,GRPO算法（一文深度解析deepseek中的强化学习算法）——手把手教你入门强化学习(九)

wxchyy

已于 2025-03-22 16:25:00 修改

阅读量2.3k

点赞数 63

分类专栏：强化学习文章标签：算法深度学习神经网络

于 2025-03-17 19:09:36 首次发布

本文链接：https://blog.csdn.net/qq_53769632/article/details/146311507

版权

强化学习专栏收录该内容

10 篇文章

订阅专栏

前言

在上期我们介绍了策略梯度（PG算法），这期我们将继续深入PG算法，从TRPO、PPO，到最后最近大火的deepseek中的强化学习算法GRPO。

前期回顾

强化学习:基础知识篇(包含Gym库的简单实践)——手把手教你入门强化学习（一）
强化学习:Markov决策过程(MDP)——手把手教你入门强化学习(二)
强化学习:实践理解Markov决策过程(MDP)——手把手教你入门强化学习(三)
强化学习:动态规划求解最优状态价值函数——手把手教你入门强化学习(四)
强化学习:蒙特卡罗求解最优状态价值函数——手把手教你入门强化学习(五)
强化学习:时间差分(TD)(SARSA算法和Q-Learning算法)——手把手教你入门强化学习(六)
强化学习:一文通透DQN算法及其变种(你要的深度强化学习算法)——手把手教你入门强化学习(七)
强化学习:策略梯度算法(PG算法族)——手把手教你入门强化学习(八)

一、理论基础

KL散度

在学习之前，首先我们需要先了解一下KL散度，KL 散度是信息论中的概念，它是用来两个概率分布差异的指标。我们先看一下公式：
在这里插入图片描述

若P和Q一致，则KL散度为0
若P和Q差异越大，则KL散度越高。
一般在强化学习中，我们比它用于新旧策略 $\pi_{old}$ 和 $\pi_{new}$ 的差异度量，防止策略突变。

KL惩罚

KL惩罚则是将KL散度作为正则项加入到目标函数中，控制策略更新的幅度。在强化学习中，我们会将KL散度作为正则项加入优化目标，限制策略更新幅度。类似这样，加在目标函数中。
在这里插入图片描述
$\beta$ :权衡策略性能与保守性的系数。
很好理解，当差异越大时，目标函数就会变小，防止因策略变换太大，目标函数急剧增大。

自然梯度

这里我就不详细展开了，简单说一下，自然梯度通过引入概率分布的几何结构，修正普通梯度的方向，使其更符合策略分布的“真实”变化，核心思想是用KL散度衡量策略分布的差异，并基于此重新定义梯度方向。主要解决了传统梯度更新方向不匹配，步长难以控制两个问题，因为在传统梯度下降中，参数的更新方向由损失函数的梯度决定，参数空间是欧氏空间（即参数变化对策略的影响是均匀的）。然而，在强化学习中，策略是一个概率分布 $\pi_{\theta}(a|s)$ ，参数空间与策略分布空间的几何结构并不一致。
简单来说，我们用自然梯度在更新策略函数的时候，能更符合策略分布的“真实”变化。
公式如下：
在这里插入图片描述
$\nabla_{\theta}L(\theta)$ 是普通梯度
F 是Fisher信息矩阵，反映策略分布的局部曲率。

Fisher矩阵度量了策略分布 $\pi_{\theta}$ 对参数 $\theta$ 变化的敏感度。

若某参数方向导致策略分布剧烈变化，Fisher矩阵在该方向上的值较大。
若某参数方向对策略分布影响微弱，Fisher矩阵在该方向上的值较小。

二、TRPO算法

在了解了KL散度，KL惩罚，自然梯度之后，我们来学习TRPO算法，TRPO是英文单词Trust Region Policy Optimization的简称，翻译成中文是“置信域策略优化”。它的主要思想就是，如果策略更新，那它必须在以旧策略为中心的“信任域”内（KL散度 ≤ δ），就是新策略更新要有个范围。我们可以看一下它的数学形式。我们希望最大化优势函数，并且新策略的性能不比旧策略差。
不过在推导数学公式之前，我们需要先了解一下重要性采样系数：
在这里插入图片描述
通过重要性采样系数，将旧策略的数据分布 “校正” 为新策略的分布。例如，旧策略选动作 A 的概率是 0.2，新策略选 A 的概率是 0.4，重要性采样系数 2 表示新策略对该动作的 “重视程度” 是旧策略的 2 倍，通过放大旧数据中该动作的优势，近似新策略的期望。
若新策略多执行优势为正的动作，少执行优势为负的动作，整体回报就会提升。因此，最大化优势函数的期望，本质是引导策略向 “高价值动作” 倾斜。
我们再看一下在旧策略下优势函数：
在这里插入图片描述
在旧策略 $a_{\pi(\theta_{k})}(S,A)$ 收集的状态 - 动作对中，某个动作 A 在状态 S 下，相较于 “平均表现” 的额外收益。

在这里插入图片描述
但是，自然梯度算法并没有直接求解这个问题，而是求解了一个近似的问题。因为如果用自然梯度算法求解的话，在高维或非线性策略空间中，KL散度的局部形状可能非二次，导致自然梯度方向不准确，同时近似可能也不是最优，甚至变差。为了解决这一个问题，我们先需要采用共轭梯度法求解自然梯度，我们看最终迭代式扩展为：
在这里插入图片描述
信任域策略优化算法则用以下方法确定j的值：j从非负整数到0,1,2,…中依次寻找首个满足期望KL散度约束并且能提升代理梯度的值。
对此，我们看一下TRPO如何进行求解的。
（1） 初始化参数:θ←任意值（策略参数），w←任意值（价值函数参数）；
（2） 时序差分更新:对每个回合执行以下操作：
1）用策略π(θ)生成轨迹；使用当前策略π(θ)与环境交互,生成轨迹数据。
2）用生成的轨迹和由w确定的价值函数估计θ处的策略梯度g和优势函数A。
优势函数：A(s,a) = Q(s,a) - $V_{\omega}(s)$ ，Q值通过TD算法求得，V值由价值网络预测产生。
策略梯度：通过轨迹数据计算，表示策略性能提升的方向。在这里插入图片描述
3 共轭梯度法求解自然梯度和最终更新量
用共轭梯度算法迭代得到x自然梯度方向，再结合信任域约束求得缩放因子得到最终更新量 $\sqrt{\frac{2\delta}{x^{T}FX}}x$ ;
4 策略更新
确定j的值，使得新策略在信任域内，并且代理优势有提升。
更新策略参数 $\theta \leftarrow \theta +\alpha_{j} \sqrt{\frac{2\delta}{x^{T}Fx}}x$
5 价值函数更新
更新w以减小价值函数的误差，最小化时序差分误差（TD Error）。
在这里插入图片描述
通过梯度下降更新w，提升优势函数估计的准确性。

三、PPO算法

由于TRPO 通过求解带 KL 散度约束的优化问题（需计算 Hessian 矩阵和共轭梯度），计算复杂度高（O (n³)），工程实现困难。在PPO（近端策略优化）算法中，引入了剪切比率以及自适应 KL 控制。
我们看一下它的具体改进：
1 它通过剪裁概率比来近似实现TRPO算法中的KL散度的约束，从而避免复杂的二阶优化。
在这里插入图片描述
其中

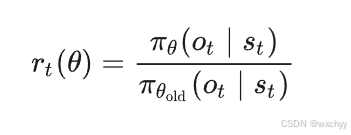
表示新旧策略在该动作上的概率比。如果该比值偏离 1 太远，它将被裁剪在 $([1-\varepsilon,1+\varepsilon]$ 范围内，这限制了策略在一次更新中可以变化的程度。
优势：无需显式计算 KL 散度和 Hessian，仅用一阶梯度下降（如 Adam），计算复杂度降至 O (n)，代码量减少 90% 以上。
2 PPO采用自适应 KL 控制，PPO-KL惩罚
TRPO 的问题：手动设定 KL 散度阈值 $\delta$ 需反复调参，过小导致收敛慢，过大易退化。
在 PPO 中，这通过添加对参考模型（初始策略）的 KL 惩罚来体现。具体来说，我们在损失函数中加入类似以下内容：
在这里插入图片描述
目标函数变为：

通过监测 KL 值自动调整 $\beta$ （如 KL 超过目标值则增大 $\beta$ ，反之减小），避免手动调参。

四、GRPO算法

GRPO算法——组相对策略优化，用“多次模拟平均值”替代价值函数，为什么要消除价值函数呢，因为PPO 依赖价值网络（Critic）估计状态价值，需同时训练策略和价值两个模型，显存占用高（如 32B 模型需额外 20GB 显存），且价值函数误差易导致策略退化。
&emsp；那我们用什么替代价值函数呢，用“多次模拟平均值”替代价值函数。直接删除 Critic，对每个输入生成K 个候选输出，用组内平均奖励作为基线计算相对优势。简单来讲，现在我们用策略函数随机生成多个输出，在再组内求个平均，作为基准。举个例子：我们做数学题前，先生成 8 个解题步骤，奖励最高的候选优势为正，最低的为负，通过组内比较消除绝对奖励偏差。我们看一下公式。
在这里插入图片描述
同时，GRPO保留了 PPO 的裁剪和 KL 机制，以确保稳定、合规的更新。我们看一下目标函数公式：

通过计算同一问题的多个输出的平均值并进行标准化，得出“相对分数”。这样，我们不再需要专用的价值函数，但仍能获得动态的“分数线”，简化训练并节省资源。
GRPO 通过砍掉价值函数、用分组替代单样本、极简奖励，在大模型时代找到了 “少即是多” 的路径：牺牲部分生成效率，换取显存、训练成本和推理质量的突破。