数字逻辑技术基础（三十八）——进制译码器

1 进制译码器

进制译码器是一种将输入的编码信号转换为特定进制的输出信号的数字电路。常见的编码器包括二-十进制译码器、BCD到十进制译码器等。

 1.1  二-十进制译码器

二-十进制译码器是将输入的BCD码转换为10个高、低电平输出信号。

真值表如下所示：

图1 二-十进制译码器的真值表

可以看到，输入是二进制的0000~1001，输出只有一位低电平有效。

总结真值表，可以得到如下逻辑式：

                               

                                

                                

                                

                                 

二-十进制译码器的电路图如下所示：

图2 二-十进制的电路图

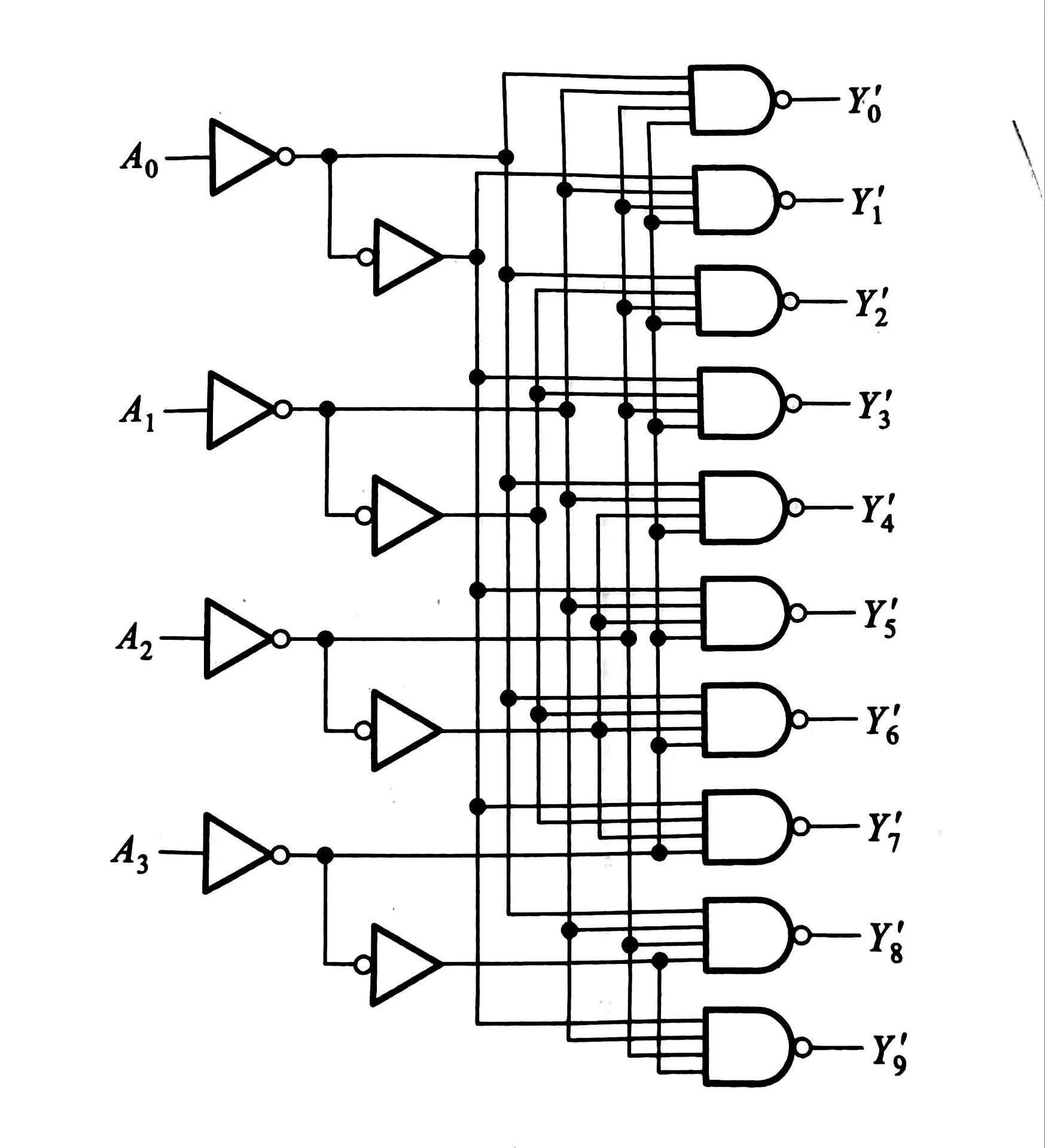
二-十进制译码器的应用包括控制7段数码管的数字显示，同时在工业控制中在PLC或者自动化设备中作为状态译码器。

1.2 8421码转换为4位循环码

如下所示电路图：

图2 8421码转换为循环码的电路图

通过上图的输入可以得到如下所示的真值表：

表1 8421码转换为4位循环码的真值表

0	0	0	0	0	0	0	0
0	0	0	1	0	0	0	1
0	0	1	0	0	0	1	1
0	0	1	1	0	0	1	0
0	1	0	0	0	1	1	0
0	1	0	1	0	1	1	1
0	1	1	0	0	1	0	1
0	1	1	1	0	1	0	0
1	0	0	0	1	1	0	0
1	0	0	1	1	1	0	1
1	0	1	0	1	1	1	1
1	0	1	1	1	1	1	0
1	1	0	0	1	0	1	0
1	1	0	1	1	0	1	1
1	1	1	0	1	0	0	1
1	1	1	1	1	0	0	0

在上图中，各个输出与输入之间的关系式如下所示：

                                                                     

                                                                     

                                                                     

                                                                     

因此输出和输入之间的关系为：

                                                                      

通过对比真值表可以看出，输出是4位循环码，本电路实现了从四个二进制数转化为4位循环码的电路。

1.3 余三码转化为8421码

四位余三码转换为8421码的真值表如下所示：

表2 4位余三码转换为8421码的真值表

				D	C	B	A
0	0	1	1	0	0	0	0
0	1	0	0	0	0	0	1
0	1	0	1	0	0	1	0
0	1	1	0	0	0	1	1
0	1	1	1	0	1	0	0
1	0	0	0	0	1	0	1
1	0	0	1	0	1	1	0
1	0	1	0	0	1	1	1
1	0	1	1	1	0	0	0
1	1	0	0	1	0	0	1

通过真值表可以推算相应的逻辑式。

（1）对与逻辑符号A：

图3 逻辑符号A的卡诺图

输出变量A的逻辑式为。

（2）对于输出变量B：

图4 逻辑符号B的卡诺图

输出变量B的逻辑式为

（3）对于输出变量C：

图5 逻辑符号C的卡诺图

输出变量C的逻辑式为

（4）对于输出变量D：

图6 逻辑符号D的卡诺图

 输出变量D的逻辑式为：。

总结上面逻辑式为：

                                                                 

                                                                  

                                                                  

                                                                  

电路结构如下所示：

图7 余三码转换为8421码的电路

运行本电路，例如当输入0101时：

图7 输入0101时的余三码转换为8421码电路图

 可以看到，当输入0101时，输出为0010，属于余三码到8421码的转换。

当输入1000时：

图8 输入1000时的余三码转换为8421码电路图

可以看到输出为1010，属于余三码到8421码的转换。

1.4 8421码转换为余三码

余三码可以转换为8421码，8421码同样也可以转换为余三码。真值表如下所示：

表3 8421码转换为余三码的真值表

				D	C	B	A
0	0	0	0	0	0	1	1
0	0	0	1	0	1	0	0
0	0	1	0	0	1	0	1
0	0	1	1	0	1	1	0
0	1	0	0	0	1	1	1
0	1	0	1	1	0	0	0
0	1	1	0	1	0	0	1
0	1	1	1	1	0	1	0
1	0	0	0	1	0	1	1
1	0	0	1	1	1	0	0

通过真值表可以推算相应的逻辑式。

（1）对于输出变量A：

图9 输出变量A的ka'nuo

输出变量A的逻辑式为。

（2）对于输出变量B：

图10 输出变量B的卡诺图

输出变量B的逻辑式为

（3）对于输出变量C：

图11 输出变量C的卡诺图

输出变量C的逻辑式为。

（4）对于输出变量D：

图12 输出变量D的卡诺图

输出变量D的逻辑式为：

可以总结为：

                                                                     

                                                                     

                                                                      

                                                                      

电路结构如下所示：

图13 8421码转换为余三码的电路图

运行本电路，当输入为0010时：

图14 当输入0010时8421码转化为余三码电路图

可以看到输出为0101，即十进制的5，符合8421码到余三码的转换。

当输入为0110时：

图15 当输入0110时8421码转换为余三码电路图

可以看到输出为1001，即十进制的9，符合8421码到余三码的转换。

当输入为1000时：

图16 当输入1000时8421码转换为余三码的电路图

可以看到输出为1011，即十进制的11，符合8421码到余三码的转换。

 2 利用74LS283实现8421码到余三码的转换

2.1 74LS283芯片介绍

74LS283芯片是一款4位全加器的集成电路芯片，属于TTL系列，能够实现高速的加法运算。

芯片的逻辑框图如下所示：

图17 74LS283的逻辑框图

74LS283芯片一共有14个引脚，其中包括四位被加数，四位加数，四位输出，进位输入和进位输出。

芯片的运行规则如下所示：

图18 74LS283的逻辑框图

74LS283芯片是CPU和计算的基本运算器件，应用较为广泛。

2.2 电路设计

现在要使用加法器实现8421码到余三码的转换，实际上就是将四位输入信号加上二进制的0011。可以把四位输入信号当作被加数，把二进制的0011当作加数，进位输入接低电平。然后直接观察输出结果即可。

如下图所示：

图19 当加数为0011的74LS283芯片

使用Multisim软件对于实现该电路得：

图20 使用Mutlisim软件模拟8421码到余三码的转换

字发生器的范围为0000~1001，频率设置为20HZ。

运行该电路，当输入为0010时：

图21 当输入0010时电路的运行结果

可以看到输出结果为0101，符合8421码转换为余三码的结果。

当输入为0110时：

图22 当输入0110时电路的输出结果

可以看出输出结果为1001，符号8421码转化为余三码的结果。

同时经过电路图可以看到，0000~1001转换为余三码之后都没有发生进位。

（本文参考了哈尔滨工业大学的《数字电子技术基础》课程内容）