字节青训入营考核十五题-Java-DNA序列编辑距离

问题

问题描述

小R正在研究DNA序列，他需要一个函数来计算将一个受损DNA序列（dna1）转换成一个未受损序列（dna2）所需的最少编辑步骤。编辑步骤包括：增加一个碱基、删除一个碱基或替换一个碱基。

---

测试样例

样例1：

输入：dna1 = "AGT",dna2 = "AGCT"
输出：1

样例2：

输入：dna1 = "AACCGGTT",dna2 = "AACCTTGG"
输出：4

样例3：

输入：dna1 = "ACGT",dna2 = "TGC"
输出：3

样例4：

输入：dna1 = "A",dna2 = "T"
输出：1

样例5：

输入：dna1 = "GGGG",dna2 = "TTTT"
输出：4

思路

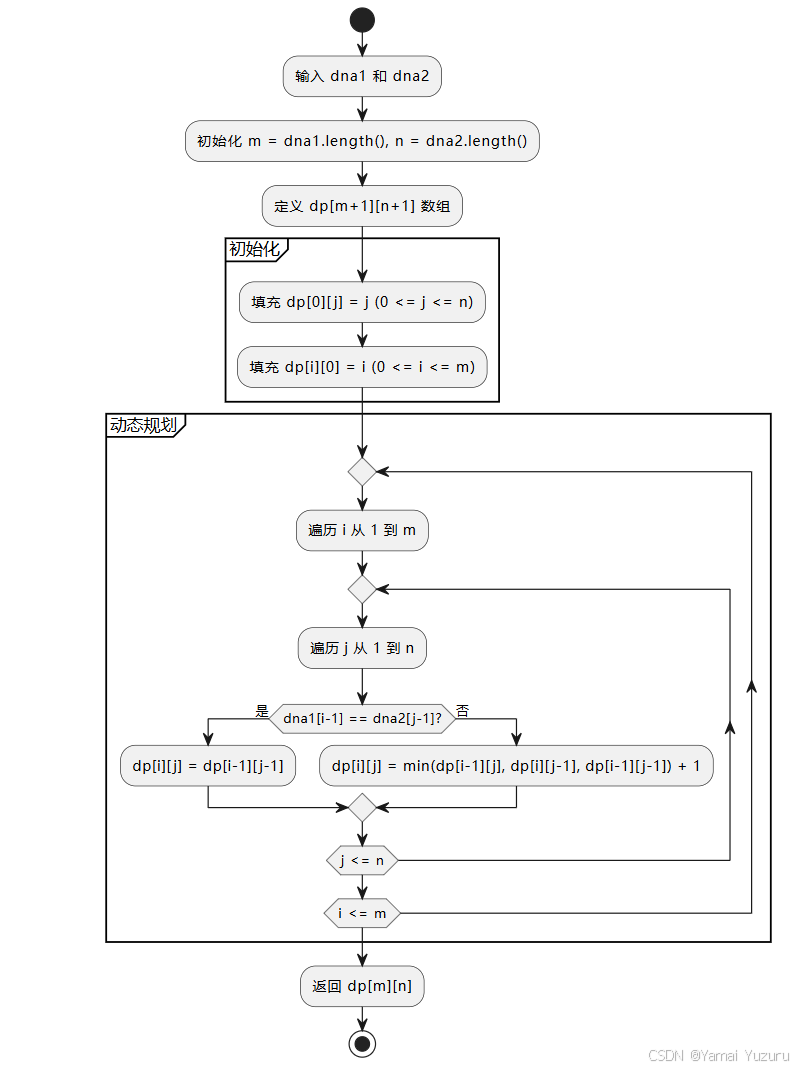
示例 1：solution("AGT", "AGCT")

• dna1 = "AGT", dna2 = "AGCT"
• 动态规划过程：
  • 初始化 dp 数组为 4x5 的矩阵（m = 3, n = 4）。
  • 填表后，dp[3][4] = 1，表示最小编辑距离是 1，即在 AGT 后插入字符 'C'。
• 输出：1

示例 2：solution("AACCGGTT", "AACCTTGG")

• dna1 = "AACCGGTT", dna2 = "AACCTTGG"
• 动态规划过程：
  • 初始化 dp 数组为 9x9 的矩阵（m = 8, n = 8）。
  • 填表后，dp[8][8] = 4，表示最小编辑距离是 4，即替换两个 'G' 为 'T'，以及插入一个 'C'。
• 输出：4

示例 3：solution("ACGT", "TGC")

• dna1 = "ACGT", dna2 = "TGC"
• 动态规划过程：
  • 初始化 dp 数组为 5x4 的矩阵（m = 4, n = 3）。
  • 填表后，dp[4][3] = 3，表示最小编辑距离是 3，替换和插入操作。
• 输出：3

示例 4：solution("A", "T")

• dna1 = "A", dna2 = "T"
• 动态规划过程：
  • 初始化 dp 数组为 2x2 的矩阵（m = 1, n = 1）。
  • 填表后，dp[1][1] = 1，表示最小编辑距离是 1，需要替换字符 'A' 为 'T'。
• 输出：1

示例 5：solution("GGGG", "TTTT")

• dna1 = "GGGG", dna2 = "TTTT"
• 动态规划过程：
  • 初始化 dp 数组为 5x5 的矩阵（m = 4, n = 4）。
  • 填表后，dp[4][4] = 4，表示最小编辑距离是 4，即替换四个 'G' 为 'T'。
• 输出：4

代码

public class Main {
    public static int solution(String dna1, String dna2) {
        int m = dna1.length();
        int n = dna2.length();
        // 定义 DP 数组
        int[][] dp = new int[m + 1][n + 1];

        // 初始化
        for (int i = 0; i <= m; i++) {
            dp[i][0] = i; // 删除操作
        }
        for (int j = 0; j <= n; j++) {
            dp[0][j] = j; // 插入操作
        }

        // 动态规划填表
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (dna1.charAt(i - 1) == dna2.charAt(j - 1)) {
                    // 当前字符相等，无需额外操作
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    // 当前字符不等，考虑插入、删除、替换操作
                    dp[i][j] = Math.min(dp[i - 1][j], 
                                 Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
                }
            }
        }

        // 返回最终结果
        return dp[m][n];
    }

    public static void main(String[] args) {
        // 测试样例
        System.out.println(solution("AGT", "AGCT")); // 输出 1
        System.out.println(solution("AACCGGTT", "AACCTTGG")); // 输出 4
        System.out.println(solution("ACGT", "TGC")); // 输出 3
        System.out.println(solution("A", "T")); // 输出 1
        System.out.println(solution("GGGG", "TTTT")); // 输出 4
    }
}

• 最小编辑距离的计算是通过动态规划来实现的，时间复杂度为 O(m * n)，其中 m 和 n 是两个字符串的长度。
• 程序通过构建一个 dp 数组逐步计算编辑距离，并在最后返回结果。

提交结果