固体微电子学与半导体物理学（三）

四、半导体载流子的平衡态统计分布

---

四、半导体载流子的平衡态统计分布

4.1 状态密度

4.1.1 三维情况下的自由电子气

4.1.2 能量状态密度

4.2 费米能级和载流子统计分布

4.2.1 费米-狄拉克(Fermi-Dirac)分布函数和玻尔兹曼(Boltzmann)分布函数

4.2.2 导带电子和价带空穴浓度

4.3 本征半导体载流子浓度的统计

4.3.1 本征载流子浓度

 4.3.2 本征费米能级位置

4.4 杂质半导体载流子统计

4.4.1 单一杂质情形

4.4.2 杂质补偿

4.5 简并半导体

---

4.1 状态密度

4.1.1 三维情况下的自由电子气

将电子困在一个边长为L的立方体里

三维情况下自由粒子遵守薛定谔方程，ψ(r）是电子波函数

要求波函数是x,y,z的周期性函数，则需要满足周期性条件

 这也就可以解释，为什么k空间中，一个允许波矢所需要的最小体积是（2π）³/V

若考虑电子的自旋，则k空间的态密度是2V/(2π)³

—— 状态密度 ：单位能量间隔内的状态数目 g(E)=dZ/dE

——K空间考虑自旋状态密度=dZ/dΩ*

4.1.2 能量状态密度

以球形等能面为例求能量状态密度

同理可得价带顶

 注意：

（1）最后得到的结果并不是约化普朗克常量

（2）状态密度与能量呈抛物线关系

（3）有效质量越大，状态密度也就越大

（4）仅适用于能带极值附近

---

一般的，晶体是各向异性的，因此其等能面是椭球面。

导带极值在k=k0处，等能面为椭球面

值得注意的是：对于硅来说有六个椭球面（六个极值），dΩ*的变化引起的体积变化应乘以6；而

锗有四个完整椭球（四个极值），则锗应该乘以4。

因此我们对各向异性晶体的能量状态密度表达式做出修正

导带：

价带：

硅与锗的价带，极值在k=0，分重空穴和轻空穴两支能带

在一维，二维，三维情况下的g(E)-E关系

4.2 费米能级和载流子统计分布

4.2.1 费米-狄拉克(Fermi-Dirac)分布函数和玻尔兹曼(Boltzmann)分布函数

费米分布函数f(E)表示：能量为 E 的一个量子态被一个电子占据的几率

玻尔兹曼分布函数：费米分布函数的特例力，适用于非简并系统，解决小概率事件问题

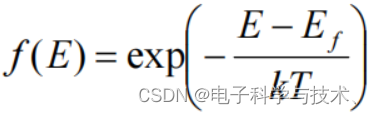
费米能级(Ef)：费米能级标志了电子填充水平，反映半导体的导电类型和参杂水平

4.2.2 导带电子和价带空穴浓度

从图上就可以看出，电子真正在的区域仅仅是导带底的一小块，而导带大部分仍是空的

 价带同理

 

 ——g(E)dE可以理解为是单位能量间隔内的空房间数，这些空房间按照f(E)的分布方式给电子占

据

——m e * ， m h * ， Eg 和 T 有关，与 EF 或掺杂浓度无关（前三项只与材料有关）

——无论本征半导体还是杂质半导体，只要是热平衡状态的非简并半导体，都适用！

4.3 本征半导体载流子浓度的统计

4.3.1 本征载流子浓度

——电中性条件：n=p=ni

 在室温下(300K)       本征载流子浓度（300K）       极限工作温度（ni＜5x10^14）

Ge：0.67eV                    ni=2.4x10^13n                             370K

Si：1.12eV                     ni=1.5x10^10                               520K

GaAs：1.43eV               ni=1.1x10^7                                 720k(高温半导体)

 4.3.2 本征费米能级位置

电中性条件n=p

 mdp和mdn同数量级，所以第二项是一个比较小的负值，可以忽略。因此我们说：本征费米能级Ei基本上在禁带中线处。

4.4 杂质半导体载流子统计

4.4.1 单一杂质情形

术语定义：

 求解载流子浓度思路：写电中性方程，只要T确定了,Ef也就确定，n0 p0也就确定了

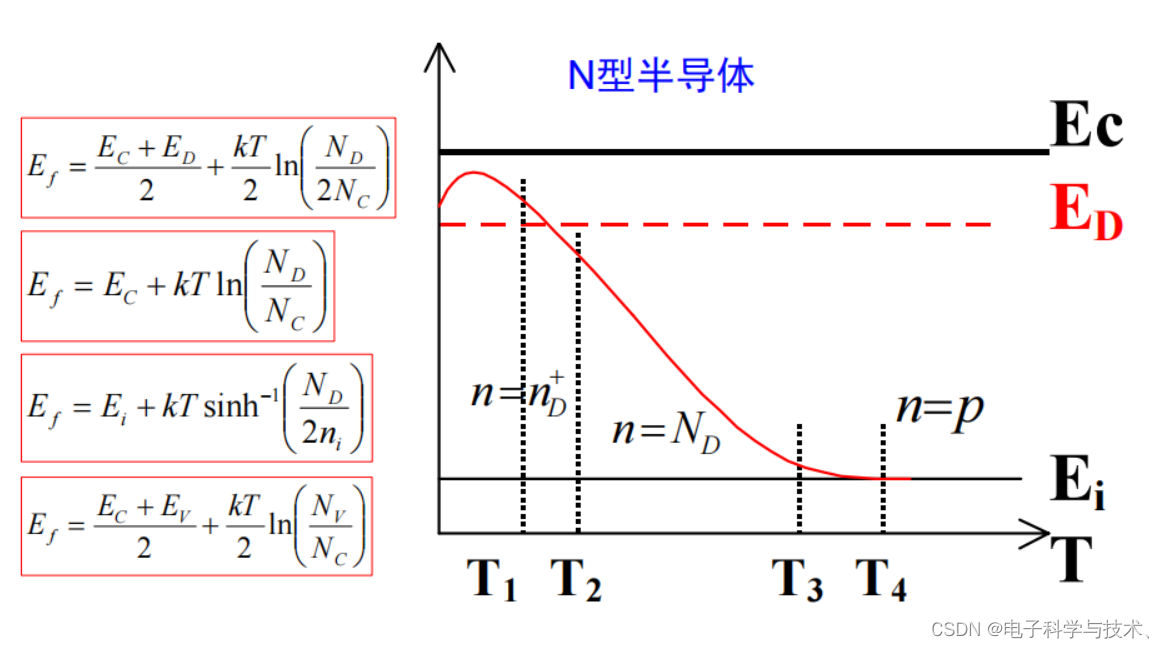
4.4.2 杂质补偿

 （从上式可以看出，仅有温度和Ef是未知的）

1）在低温弱点离区，Ef钉扎在ED附近，此时的电中性方程可以写为

ND=n0+NA+nD：施主电子一部分用于补偿受主能级，一部分用于导带导电，一部分留在施主能级上

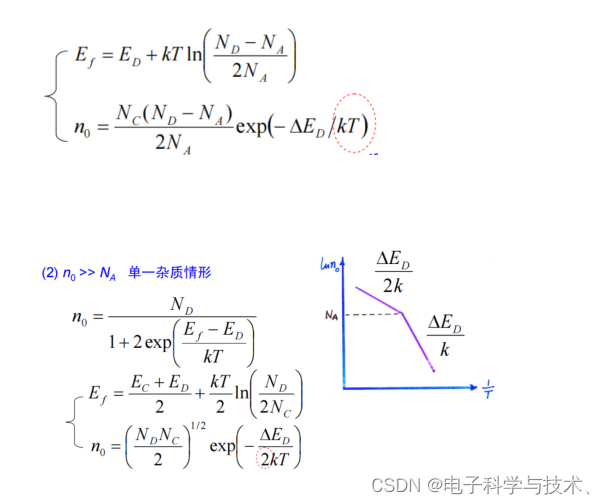
2）强电离区：ND - NA >> ni

3）过渡区（考虑本征激发） 

4.5 简并半导体

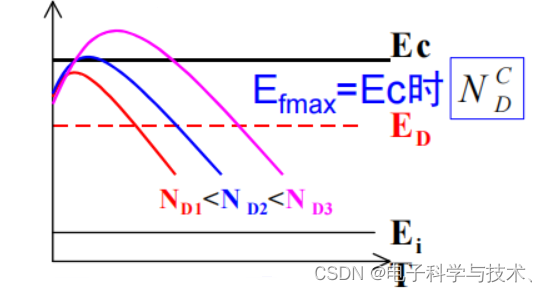
——简并化：参杂浓度过高，费米能级进入导带。杂志不能完全电离，需要考虑泡利不相容原理。随着掺杂浓度升高，费米能级的极大值点对应的温度

值也会升高。

——简并判据：

 ——强简并条件（定量）

1  发生简并时，ND ≥ ~ N C ~ 10^19 cm-3 重掺杂

2  ND 之值与 Δ ED，m e* 有关

3  ND 之值与 T 有关 ，Δ ED越小，发生简并化的浓度越小

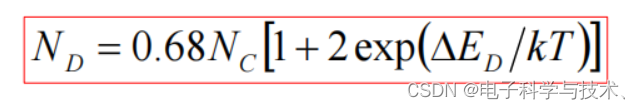
——禁带变窄效应：简并半导体中杂志能及扩展为能带并进入导带，与导带相连，形成新的简并导带，使能带边缘延伸，导致禁带宽度变窄。本征载流子浓度因禁带变窄而增加

---

本章是半导体物理计算的基础。需要重点推导不同温区的各个公式。由于内容数量庞大，一些公式本文不做具体推导，只给出结论。想深入了解的同学请自行推导

---