自适应信号检测——GLRT, AMF, Rao test, Wald test的解析和对比

最新推荐文章于 2024-07-14 18:15:43 发布

XD_MaoHai

最新推荐文章于 2024-07-14 18:15:43 发布

阅读量2.6k

点赞数 26

分类专栏：雷达数据处理文章标签：算法信号处理目标检测

本文链接：https://blog.csdn.net/qq_56937808/article/details/135489324

版权

雷达数据处理专栏收录该内容

2 篇文章 5 订阅

订阅专栏

三、广义似然比检测（Generalized Likelihood Ratio Test, GLRT）

3.1 检测器推导

3.2 GLRT性能参数

3.3 GLRT性能讨论

四、自适应匹配滤波检测（Adaptive Matched Filter Test, AMF Test）

4.1 检测器推导

4.2 AMF检测性能参数

4.3 GLRT和AMF检测性能对比

五、Wald检测和Rao检测（Wald Test and Rao Test）

5.1 检测器表达式

5.2 Wald和Rao检测性能参数

5.3 GLRT、AMF和Rao检测性能对比

参考文献

一、引言

自适应在进化论中指的是生物体或种群更好地适应环境的过程或特征，同样在信号处理领域，自适应信号检测可理解为检测器（生物体）在未知时变的杂噪和干扰背景（生存环境）中适应性的做出判决的过程。这种通过学习环境而自适应更新进化的特征在检测器中体现为利用基于样本数据的估计值替代未知参数的操作，而通过不同的替代或近似过程可以得到不同的自适应检测器，其中比较典型的包括广义似然比检测（Generalized Likelihood Ratio Test, GLRT），自适应匹配滤波检测（Adaptive Matched Filter Test, AMF Test）,Wald和Rao检测。本文主要就笔者近期的学习对这几种自适应检测器作以总结分析和性能对比，有不当之处还请斧正。

此外，本文所出现的图线均来自文末的参考文献，本文引用时会标明出处，如有侵权请联系删除。

二、非相干积累检测器和性能参数

本节主要对非相干融合检测器进行分析介绍，并对其性能参数给出理论结果。

2.1 非相干积累检测器

假设接收器对目标进行了N次独立采样，每次采样的复信号在不同假设条件下的表示形式为：

$z[n]=\left\{\begin{matrix} s[n]+w[n] & ,H_1\\ w[n] & ,H_0 \end{matrix}\right.,\\ n=1,\cdots,N.$

其中s[n]表示目标信号复标量幅度，其根据不同的目标起伏模型服从不同的分布。w[n]表示服从零均值复高斯分布的杂噪部分，功率为 $\sigma_{w}^{2}$ 。假设目标非起伏（Swerling 0或5），即s[n]为常数，则信号幅值的似然概率密度函数为[2]：

$p(|z[n]|)=\left\{\begin{matrix} \frac{2|z[n]|}{\sigma_{w}^{2}}e^{-|z[n]|^{2}/\sigma_{w}^{2}} & ,H_{0}\\ \frac{2|z[n]|}{\sigma_{w}^{2}}e^{-(|z[n]|^{2}+|s[n]|^{2})/\sigma_{w}^{2}}I_{0}(\frac{2|s[n]||z[n]|}{\sigma_{w}^{2}}) & ,H_{1} \end{matrix}\right.$

上式中 $H_1$ 假设条件下的概率密度函数称为莱斯分布，其中 $I_{0}(\cdot)$ 为修正的零阶第一类贝塞尔函数，该分布从某一门限到正无穷的积分（该条件下的检测概率）是雷达检测计算中常用的Marcum的Q函数(Marcum Q-function)，但该积分至今仍未得到闭式解。

由于各采样值独立同分布，因此由N个样本的幅值构成的矢量z的似然概率密度函数为：

$p(\mathbf{z}|H_{0})=\prod_{n=1}^{N}p(|z[n]|\mid H_{0}),\\ p(\mathbf{z}|H_{1})=\prod_{n=1}^{N}p(|z[n]|\mid H_{1})$

基于Neyman-Person准则可以得到最优检验统计量为：

$l(\mathbf{z})=\frac{p(\mathbf{z}|H_{1})}{p(\mathbf{z}|H_{0})}=\sum_{n=1}^{N}\ln[I_{0}(\frac{2|s[n]||z[n]|}{\sigma_{w}^{2}})]$

为避免未知量对检测的影响以及复杂的对数计算，利用平方律检波器替代上述检验统计量并省去常数项可得到非相干积累检验统计量：

$u=\sum_{n=1}^{N}|z[n]|^{2}/\sigma_{w}^{2}$

可以看到，该检验统计量u是各采样信号归一化功率（观测信噪比）之和，其概率密度函数为[1]：

$f_{N}(u,a)=e^{-u-a}(u/a)^{(N-1)/2}I_{N-1}(2\sqrt{au})$

其中 $I_{N-1}(\cdot)$ 表示修正的N-1阶第一类贝塞尔函数，a表示目标信号归一化功率之和：

$a=\sum_{n=1}^{N}|s[n]|^{2}/\sigma_{w}^{2}$

易知 $H_{0}$ 条件下a的值为0，此时u服从自由度为2N的卡方分布(厄兰密度)：

$g_{N}(u)=f_{N}(u,0)=\frac{u^{N-1}}{(N-1)!}e^{-u}$

特别的，当N=1时， $g_{1}(u)$ 为指数分布（瑞利变量的平方服从的分布）， $f_{1}(u,a)$ 为服从广义偏正卡方分布（莱斯变量的平方服从的分布）。

当目标散射截面积发生起伏时，目标信号幅值不再为常数，则此时a服从的概率密度函数为：

$f_{0}(a)=\frac{1}{b}g_{M}(\frac{a}{b})=\frac{1}{b}\frac{(a/b)^{M-1}}{(M-1)!}e^{-a/b}$

其中2M表示卡方分布的自由度，b表示独立信号总信噪比，假设单采样点信号的归一化功率均值为1，则不同起伏模型下的M和b的值为：

不同目标起伏模型下的M值和b值
Swerling 模型	M	b
Swerling 1	1	N
Swerling 2	N	1
Swerling 3	2	N/2
Swerling 4	2N	1/2

这样一来目标信号归一化功率之和的均值为：

$\bar{a}=\rm Mb$

由此可给出平均信噪比定义为：

$\rm SNR=\frac{\bar{a}}{N}=\frac{Mb}{N}$

这是Kelly用来描述Swerling模型的方式，也是笔者认为巧妙的地方，也即用两个参数来表示目标信号样本的非相参功率之和的分布，比较方便理解和记忆。

我们得到非相干积累的检验统计量后，令其与某一门限y作比较从而得到非相干积累检测器：

$u\begin{matrix} H_{1}\\ >\\ <\\ H_{0} \end{matrix}y$

与目标信号的建模一致，根据实际应用的不同，门限y也可建模为固定值或浮动值，当y为浮动值时，我们常会发现这种情况下的检测器虚警概率与杂噪的协方差矩阵无关，这是因为用以估计协方差矩阵的次要数据（Secondary data）和检测单元数据（Primary data）具有相同的杂噪背景， $H_{0}$ 假设条件下通过白化和归一（3.2节会介绍）的操作可将检测器两端的数据转换为不依赖杂噪协方差矩阵的单位数据，这种性质也是我们熟知的恒虚警率（Constant False Alarm Rate, CFAR）。

当门限值y为浮动值时，可将其建模为：

$y=cx$

其中c为标量值，x表示浮动参数，一般将x建模为自由度为2L的卡方分布：

$x\sim g_{L}(x)$

则门限值的分布为：

$y\sim \frac{1}{c}g_{L}(\frac{y}{c})$

2.2 非相干积累检测器性能参数

本小节对目标信号和门限不同浮动情况下非相干积累检测器的检测概率和虚警概率给出理论结果，具体推导过程可参文献[1]。

（1）固定目标，固定门限

$P_{\rm D}=\int_{y}^{+\infty}f_{N}(u,a){\rm d}u\\ P_{\rm fa}=S_{N}(y)=\int_{y}^{+\infty}f_{N}(u,0){\rm d}u=e^{-y}\sum_{n=0}^{N-1}\frac{y^{n}}{n!}$

其中检测概率 $P_{\rm D}$ 可借助Marcum的Q函数进行求解。特别的，当N为1时（只有一个检测样本），虚警概率简化为我们熟知的指数形式 $e^{-y}$ 。

（2）固定目标，浮动门限

$P_{\rm D}=1-\frac{c^{N}}{(1+c)^{N+L-1}}\sum_{l=0}^{L-1}{\rm C}_{N+L-1}^{N+l}c^{l}S_{l+1}(\frac{a}{1+c})\\ P_{\rm FA}=\frac{1}{(1+c)^{N+L-1}}\sum_{l=0}^{N-1}{\rm C}_{N+L-1}^{l}c^{l}$

特别的，当N为1时，虚警概率简化为单元平均恒虚警检测器的虚警概率 ${(1+c)^{-L}}$ 。

（3）浮动目标，固定门限

该情况下虚警概率和（1）中一致，不同起伏模型下的检测概率为：

① $M=N(\rm Swerling\ 2):$

$P_{\rm D}=S_{N}(\frac{y}{1+b})$

② $M=2N(\rm Swerling\ 4):$

$P_{\rm D}=\frac{1}{(1+b)^{N}}\sum_{l=0}^{N}{\rm C}_{N}^{l}b^{l}S_{N+1}(\frac{y}{1+b})$

③ $M=1(N\geq2)(\rm Swerling\ 1):$

$P_{\rm D}=S_{N-1}(y)+(\frac{b+1}{b})^{N-1}e^{-\frac{y}{b+1}} (1-S_{N-1}(\frac{by}{1+b}))$

④ $M=2(N\geq3)(\rm Swerling\ 3):$

$P_{\rm D}=S_{N-2}(y)+(\frac{b+1}{b})^{N-2}e^{-\frac{y}{b+1}} \{(1-\frac{N-2}{b})[1-S_{N-2}(\frac{by}{1+b})]+\frac{y}{1+b}[1-S_{N-3}(\frac{by}{1+b})]\}$

特别的，当M=N=1时，检测概率简化为我们熟知的Swerling 1（或2）下的指数形式 $e^{\frac{y}{1+b}}$ 。事实上，在③的条件下，当虚警概率远小于1且信噪比较大时，检测概率可以近似为：

$\underset{P_{\rm FA}\ll 1,b \gg 1 }{\lim} P_{\rm D}=(\frac{b+1}{b})^{N-1}e^{-\frac{y}{b+1}}$

（4）浮动目标，浮动门限

该情况下虚警概率和（2）中一致，检测概率只给出以下常用的两种起伏模型下的情况：

① $M=N(\rm Swerling\ 2):$

$P_{\rm D}=(\frac{1+b}{1+b+c})^{L}\sum_{n=0}^{N-1}{\rm C}_{L+n-1}^{n}(\frac{c}{1+b+c})^{n}$

② $M=1(\rm Swerling\ 1):$

$P_{\rm D}=\frac{(1+b)^{N+L-1}}{b^{N-1}(1+b+c)^{L}}+\frac{1}{(1+c)^{N+L-1}}\sum_{l=0}^{N+L-1}{\rm C}_{N+L-1}^{{l}}c^{l}[1-(\frac{b}{1+b+c})^{l+1-N}]$

特别的，当 $M=N=1$ 时，检测概率简化为Swerling 1（或2）下单元平均恒虚警检测器的检测概率 $(1+\frac{c}{1+b})^{-L}$ 。

需要注意的是，以上的非相干积累检测有一个必要性的假设就是N个目标样本值的杂噪信号独立同分布，且各样本值的目标平均信噪比一致，因此检验统计量为各样本归一化功率的等权重加和。但是当各样本值的杂噪信号不再独立且功率不一致时，则需要利用另外的方式进行检测器设计，例如以下的GLRT。虽然检测器形式不一致，但幸运的是，经过一些数理推导后，这些检测器的性能参数可以化简为以上非相干积累检测的性能参数的相关结果，这也是笔者为何要把这一章节放在前面的一个原因。

三、广义似然比检测（Generalized Likelihood Ratio Test, GLRT）

我们知道在Neyman-Person准则下，最优检验统计量是似然比的形式：

$l_{\rm opt}(\mathbf{z})=\frac{P(\mathbf{z}|H_{1},\theta_{1})}{P(\mathbf{z}|H_{0},\theta_{0})}$

其中z表示观测数据， $\theta_{1},\theta_{0}$ 分别表示在 $H_{1},H_{0}$ 假设条件下的未知参数，为了求解这些未知参数，可以利用这些参数的极大大似然估计值进行替代，此时检验统计量为：

$l_{\rm GLRT}(\mathbf{z})=\frac{\underset{\theta_{1}}{\rm max} P(\mathbf{z}|H_{1},\theta_{1})}{\underset{\theta_{0}}{\rm max}P(\mathbf{z}|H_{0},\theta_{0})}$

而这就是GLRT。

3.1 检测器推导

假设某 $N\times 1$ 的待检测复矢量(Primary data)为 $\mathbf{z}$ ，该矢量可以是由 $N_{a}$ 个阵元和 $N_{p}$ 个脉冲对某一距离门的复数观测数据组成的矢量，也即有 $N=N_{a}N_{p}$ 。次要数据(Secondary data)由相邻K个距离门的观测复矢量组成，即 $\{\mathbf{z}(k) \in \mathbb{C}^{N\times1}|,k=1,2,\cdots,K\}$ 。在不同的假设条件下，可将上述数据建模为：

$\left\{\begin{matrix} \mathbf{z}=\left\{\begin{matrix} b\mathbf{s}+\mathbf{w}&,H_{1}\\ \mathbf{w}&,H_{0} \end{matrix}\right.\\ \mathbf{z}(k)=\mathbf{w}(k),H_{1}\ {\rm and}\ H_{0} \end{matrix}\right.$

其中b表示未知的复标量幅度，s表示目标信号的归一化矢量，其中包含了阵列的相位信息、多普勒信息以及未知的扰动信息，在文献[3]中该矢量被建模为了已知的导向矢量。事实上，笔者认为，虽然我们无法得知目标的多普勒和导向矢量信息，但一般实际工程中是通过滤波器组对多普勒维和空间维进行搜索，搜索过程中多普勒通道和空间谱通道形成的确定相位矢量就可认为是s。其实，可以从后续的结果中看到，GLRT检验统计量就是一个滤波器的形式，因此此处将s建模为已知的是合理的。

$\mathbf{w},\mathbf{w}(k)\in \mathbb{C}^{N\times 1}$ 是背景杂噪矢量，假设其服从相同的零均值复高斯矢量分布，因此有：

$f[\mathbf{z}(k)]=\frac{1}{\pi^{N}\left \| \mathbf{M} \right \|}e^{-\mathbf{z}(k)^{H}\mathbf{M}^{-1}\mathbf{z}(k)},\\ f(\mathbf{z})=\left\{\begin{matrix} \frac{1}{\pi^{N}\left \| \mathbf{M} \right \|}e^{-(\mathbf{z}-b\mathbf{s})^{H}\mathbf{M}^{-1}(\mathbf{z}-b\mathbf{s})} & ,H_{1}\\ \frac{1}{\pi^{N}\left \| \mathbf{M} \right \|}e^{-\mathbf{z}^{H}\mathbf{M}^{-1}\mathbf{z}} & ,H_{0} \end{matrix}\right.$

其中M表示杂噪的协方差矩阵：

$M=E[\mathbf{w}\mathbf{w}^{H}]=E[\mathbf{w}(k)\mathbf{w}(k)^{H}]$

此时观测数据的似然联合概率密度分别为：

$H_{0}:f_{0}[\mathbf{z},\mathbf{z}(1),\cdots,\mathbf{z}(k)]=\{\frac{1}{\pi^{N}\left \| \mathbf{M} \right \|}e^{-{\rm tr}(\mathbf{M}^{-1}\mathbf{T}_{0})}\}^{K+1},\\ H_{1}:f_{1}[\mathbf{z},\mathbf{z}(1),\cdots,\mathbf{z}(k)]=\{\frac{1}{\pi^{N}\left \| \mathbf{M} \right \|}e^{-{\rm tr}(\mathbf{M}^{-1}\mathbf{T}_{1})}\}^{K+1}$

其中：

$T_{0}=\frac{1}{K+1}(\mathbf{z}\mathbf{z}^{H}+\sum_{k=1}^{K}\mathbf{z}{(k)}\mathbf{z}{(k)}^{H}),\\ T_{1}=\frac{1}{K+1}((\mathbf{z}-b\mathbf{s})(\mathbf{z}-b\mathbf{s})^{H}+\sum_{k=1}^{K}\mathbf{z}{(k)}\mathbf{z}{(k)}^{H})$

根据复高斯矢量的协方差矩阵极大似然估计公式可知有：

$\underset{\mathbf{M}}{\rm max}f_{0}=f_{0}|_{\mathbf{M}=\mathbf{T}_{0}}=(\frac{1}{(e\pi)^{N}\left \| \mathbf{T}_{0} \right \|})^{K+1},\\ \underset{\mathbf{M}}{\rm max}f_{1}=f_{1}|_{\mathbf{M}=\mathbf{T}_{1}}=(\frac{1}{(e\pi)^{N}\left \| \mathbf{T}_{1} \right \|})^{K+1}$

在 $H_{1}$ 假设条件下还存在未知参数b，对其进行极大似然估计有[3]：

$\widehat{b}=\frac{\mathbf{s}^{H}\mathbf{S}^{-1}\mathbf{z}}{\mathbf{s}^{H}\mathbf{S}^{-1}\mathbf{s}}$

其中：

$\mathbf{S}=\sum_{k=1}^{K}\mathbf{z}(k)\mathbf{z}(k)^{H}$

这里需要注意的是，当K>N时，S会以概率1非奇异，这也是我们后面的一个假设条件。

将上述关于M和b的估计值带入到似然函数中并作似然比，经过一些运算和省去常数项后得到最后的GLRT检验统计量为：

$\eta=\frac{|\mathbf{s}^{H}\mathbf{S}^{-1}\mathbf{z}|^2}{(\mathbf{s}^{H}\mathbf{S}^{-1}\mathbf{s})[1+(\mathbf{z}^{H}\mathbf{S}^{-1}\mathbf{z})]}$

令其与一门限比较可得到GLRT检测器形式：

$\eta \begin{matrix} H_{1}\\ >\\ <\\ H_{0} \end{matrix}\eta_{0}$

讨论：有色滤波器

若用 $\widehat{\mathbf{M}}$ 表示基于次要数据的协方差矩阵估计值：

$\widehat{\mathbf{M}}=\frac{1}{K}S$

则有GLRT检验统计量为：

$\eta=\frac{|\mathbf{s}^{H}\widehat{\mathbf{M}}^{-1}\mathbf{z}|^2}{(\mathbf{s}^{H}\widehat{\mathbf{M}}\mathbf{s})(1+\frac{1}{K}\mathbf{z}^{H}\widehat{\mathbf{M}}^{-1}\mathbf{z})}$

注意到此时若给出如下的权系数定义：

$\widehat{\mathbf{w}}=\widehat{\mathbf{M}}^{-1}\mathbf{s}$

则检验统计量分子可重写为：

$l_{\rm RMB}=|\mathbf{s}^{H}\widehat{\mathbf{M}}^{-1}\mathbf{z}|^2=|\widehat{\mathbf{w}}^{H}\mathbf{z}|^2$

其中 $l_{\rm RMB}$ 就是文献[4]提出的有色滤波器输出的信号功率，同时也可用作检验统计量进行门限检测。其实如果对阵列信号处理有过了解，不难得知有色滤波器权系数 $\widehat{\mathbf{w}}$ 就是最大信噪比加权准则下最优权系数的估计值，文献[3]有对该滤波器进行详细描述和收敛性分析。

3.2 GLRT性能参数

讨论：数据的白化和归一

在进行GLRT性能参数推导之前，我们不妨先来学习下数据白化(Whitening)和归一(Normalization)的概念。假设某随机矢量为 $\mathbf{y}$ ，其协方差矩阵为：

${\rm Cov}(\mathbf{y},\mathbf{y})=\mathbf{Q}$

由于 $\mathbf{Q}$ 为厄密矩阵( $\mathbf{Q}=\mathbf{Q}^{H}$ )，因此可以对其进行酉对角化：

$\mathbf{Q}=\mathbf{P}\mathbf{\Lambda} \mathbf{P}^{H}= (\mathbf{P}\mathbf{\Lambda}^{1/2})(\mathbf{P}\mathbf{\Lambda}^{1/2})^{H}=\mathbf{T}\mathbf{T}^{H}$

其中 $\mathbf{P}$ 为酉矩阵，每列对应 $\mathbf{Q}$ 的特征向量。 $\mathbf{\Lambda}$ 为对角矩阵，对角元素为 $\mathbf{Q}$ 的特征值。不妨构造新的数据矢量：

$\mathbf{x}=\mathbf{T}^{-1}\mathbf{y}=\mathbf{\Lambda}^{-1/2}\mathbf{P}^{H}\mathbf{y}$

则新数据矢量 $\mathbf{x}$ 的协方差矩阵为：

${\rm Cov}(\mathbf{x},\mathbf{x})=\mathbf{\Lambda}^{-1/2}\mathbf{P}^{H}\mathbf{Q}\mathbf{P}\mathbf{\Lambda}^{-1/2}=\mathbf{\Lambda}^{-1/2}\mathbf{P}^{H} \mathbf{P}\mathbf{\Lambda} \mathbf{P}^{H}\mathbf{P}\mathbf{\Lambda}^{-1/2}=\mathbf{I}$

可以看到经过线性变化后的 $\mathbf{y}$ 各变量间不相关且方差为单位1，此时的新数据矢量 $\mathbf{x}$ 方便分析和操作。

其实，这个变换矩阵为 $\mathbf{T}^{-1}$ 的线性变换包含了两步骤操作，第一步就是旋转操作，对应酉矩阵 $\mathbf{P}^{H}$ ，旋转之后的数据矢量各变量间不相关，因此这个过程称为数据白化。第二步是放缩操作，对应对角矩阵 $\mathbf{\Lambda}^{1/2}$ ，放缩之后各不相关的变量的方差均为1，因此这个过程称为数据归一。

其实，我们也能通过白化和归一的过程理解特征值和特征向量的概念和物理意义。首先旋转操作是 $\mathbf{P}^{H}\mathbf{y}$ ，这个式子的结果对应的矢量元素就相当于数据矢量 $\mathbf{y}$ 向各个特征向量的投影长度，也即旋转操作后的得到的矢量 $\mathbf{x}$ 是矢量 $\mathbf{y}$ 在以N个特征向量为基的线性空间内的坐标，则N个特征向量就相当于将原数据矢量线性变换到互不相关的N个变量的N个组合系数，也即变换方向。而投影后的长度就相当于新变量的标准差，为了将这些互不相关的变量的方差归一化，需要对各变量进行放缩，放缩系数大小就是特征值的平方根，而 $\mathbf{\Lambda}^{1/2}$ 的对角元素正好就是放缩系数。

首先，对杂噪协方差矩阵进行特征分解：

$\mathbf{M}=\mathbf{U\Lambda U}^{H}$

且定义：

$\mathbf{M}^{1/2}=\mathbf{U}\mathbf{\Lambda}^{1/2}\mathbf{U}^{H}$

对待检测矢量以及次要数据矢量白化归一：

$\mathbf{x}=\mathbf{M}^{-1/2}\mathbf{z},\\ \mathbf{x}(k)=\mathbf{M}^{-1/2}\mathbf{z}(k),k=1,2,\cdots,N$

需要说明的是这里的白化归一变换相较于本小节开头提到的白化归一变换多出了一步旋转操作，笔者认为这是为了方便用符合厄密特性的 $\mathbf{M}^{1/2}$ 表示，有没有这一步不影响最后的分析结果，因为白化归一后的数据进行旋转后依旧是白化归一的。

此时根据高斯矢量线性变换不变性，得到的新数据矢量依旧服从复高斯矢量分布，且得到的新数据矢量的协方差矩阵均为单位阵。

定义：

$\mathbf{t}=\mathbf{M}^{-1/2}\mathbf{s},\\$

由于有复标量b的存在，我们可以令相位矢量s满足如下的归一化：

$\mathbf{t}^{H}\mathbf{t}=\mathbf{s}^{H}\mathbf{M}^{-1}\mathbf{s}=1$

此时有：

$a=|b|^2=E[\mathbf{z}]\mathbf{M}^{-1}E[\mathbf{z}]=b\mathbf{s}\mathbf{M}^{-1}b\mathbf{s}$

可以看到，上式最后一个等号右边的式子就是最大信噪比准则下的输出信噪比，也即文献[4]中提到的输出信噪比，因此采用如上对s的最小化的好处就是，此时 $|b|^2$ 的物理意义就是信噪比值。

以上提到白化归一后的数据进行旋转后依旧是白化归一的，因此我们不妨对 $\mathbf{x},\mathbf{x}(k)$ 再次利用酉矩阵 $\mathbf{U}$ 进行旋转，且使得 $\mathbf{U}$ 满足：

$\mathbf{Ut}=\mathbf{e}_{1}$

其中 $\mathbf{e}_{1}$ 的第一个元素为1，其余为0。其实这步操作可以理解为相位匹配， $\mathbf{U}$ 的各行对应一个滤波器，且第一行对应的是与 $\mathbf{t}$ 相位匹配的滤波器，其余行的滤波器系数与t正交。这样以来就可以对各矢量和矩阵进行分块，方便计算分析。

需要提出的是，为了简化表示，利用 $\mathbf{U}$ 对 $\mathbf{x},\mathbf{x}(k),\mathbf{t}$ 变换后的矢量表示符号依旧不变。

之后定义新数据矢量协方差矩阵估计值为：

$\mathbf{Q}=\sum_{k=1}^{K}\mathbf{x}(k)\mathbf{x}(k)^{H}=\mathbf{U}\mathbf{M}^{-1/2}\mathbf{S}\mathbf{M}^{-1/2}\mathbf{U}^{H}$

此时Q服从Wishart分布，表示为 $CW(\mathbf{K},\mathbf{N};\mathbf{I})$ 。

此时3.1节中GLRT检验统计量为：

$\eta=\frac{|\mathbf{t}^{H}\mathbf{Q}^{-1}\mathbf{x}|^2}{(\mathbf{t}^{H}\mathbf{Q}^{-1}\mathbf{t})[1+(\mathbf{x}^{H}\mathbf{Q}^{-1}\mathbf{x})]}$

可以看到，上式中并没有出现杂噪协方差矩阵 $\mathbf{M}$ ，同时各随机变量，矢量或矩阵的协方差矩阵均为单位值或单位矩阵，因此将原GLRT检验统计量化为上式形式，一方面可以显现出GLRT检测器具有CFAR性质，另一方面便于之后的推导分析。

之后经过一些数理推导和等价关系后[5]，可以得到最后的GLRT检测器形式为：

$|q|^{2}>(l_{0}-1)\sum_{k=1}^{K+1-N}|q(k)|^2$

其中 $l_{0}$ 为常数，与原始检测门限关系为：

$\eta_{0}=\frac{l_{0-1}}{l_{0}}$

$q(k),k=1,2,\cdots,K+1-N$ 服从独立的标准复高斯分布。 $q$ 的分布为：

$q\sim \left\{\begin{matrix} N(br,1) & ,H_{1}\\ N(0,1) & ,H_{0} \end{matrix}\right.$

其中r为随机信噪比损失因子，也可理解为目标的起伏参数，文献[3—5]均给出了该损失因子的分布为beta分布：

$f(r)=\frac{(N+L-1)!}{L!(N-2)!}(1-r)^{N-2}r^{L}$

其中 $L=K+1-N$ 。信噪比损失均值为：

$E[r]=\frac{K+2-N}{K+1}$

因此为使得信噪比损失小于3dB，次要数据样本量需要满足 $K\geq2N-3\approx 2N$ 。

此时我们不难看到，简化后的检测器就是2.2节中门限浮动的非相参积累检测器，门限服从自由度为 $2(K+1-N)$ 卡方分布。不妨先将信噪比损失因子r和b设置为定值，则该情况下的检测器就是单目标采样点下的固定目标信号，门限浮动的非相参接力检测，也即2.2情况（2）中N=1的特殊情况，因此虚警概率和条件检测概率（“条件”是指r为定值）为：

$P_{\rm FA}=(\frac{1}{l_{0}})^{K+1-N},\\ P_{\rm D}(r,b)=1-\frac{1}{l_{0}^{L}}\sum_{k=1}^{L}{\rm C}_{L}^{k}(l_{0}-1)^{k}S_{k}(\frac{ra}{l_{0}})$

可见虚警概率和杂噪协方差矩阵无关，因此符合CFAR特性。此外，由于r为随机变量，为求解r值还需要对条件检测概率进行期望求解：

$P_{\rm D}(b)=1-\frac{1}{l_{0}^{L}}\sum_{k=1}^{L}{\rm C}_{L}^{k}(l_{0}-1)^{k}H_{k}(\frac{ra}{l_{0}})$

其中：

$H_{k}(y)=\int_{0}^{1}S_{k}(ry)f(r){\rm d}r$

该积分为多项式积分，但文献[5]中指出该结果依旧不简单，因此也没有给出具体结果，但可写成有限和的形式。

若假设目标有起伏且服从Swerling I模型，则检测概率为：

$P_{\rm D}=\int_{0}^{+\infty}P_{\rm D}(b){\rm d}b=(\frac{1+\bar{b^{2}}}{l_{0}+\bar{b^{2}}})^{L}$

这个公式就是我们常见的Swerling I模型下复标量CFAR的检测概率公式。

3.3 GLRT性能讨论

从3.2中的结果可以看到，相对于匹配滤波检测器（也即杂噪协方差矩阵准确已知）而言，GLRT检测器的性能损失主要体现在两部分，一方面是信噪比损失因子r对检测的影响，另一方面是CFAR特性带来的门限估计不准确。为了分析信噪比损失和CFAR损失，文献[5]中给出了不同参数下，匹配滤波检测器（无性能损失，性能参数对应2.2.(1)中N=1的情况），标量CFAR检测器（无信噪比损失，r=1且参考单元数量为L，性能参数对应2.2.(2)中N=1的情况）以及GLRT检测器的ROC曲线对比图如下：

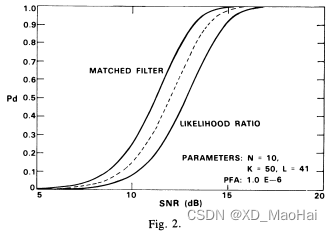
从实验结果中可以得到如下结论：

对比匹配滤波器和标量CFAR检测器（中间虚线），文献[5]中指出CFAR损失主要跟次要样本数量K值有关，且当K值增大时，CFAR损失越小。但并没有做保持L不变而增大K的消融实验，因此笔者感觉影响CFAR损失的应该是L，毕竟简化后GLRT检测器的门限值是自由度为2L的卡方分布。
SNR损失主要跟K/N值有关，且当K/N值增大时，信噪比损失越小。

此外，文献[5]还给出了相同虚警概率不同参数下，为达到与匹配滤波检测器相同的检测概率，GLRT检测器所需的额外信噪比值，也即相对于匹配滤波检测器的检测性能损失（包括信噪比损失与CFAR损失的综合损失）随K值的变化曲线：

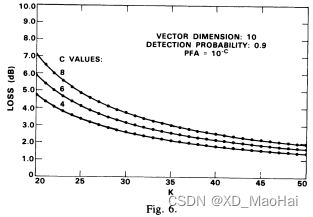
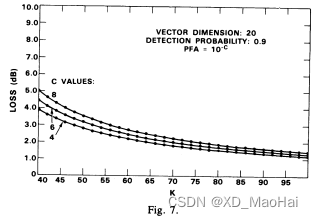
从图中可以看到，GLRT检测器的检测性能损失并不是严格关于K/N的函数，当K/N固定时，我们可以看到性能损失大体上随着N的递增而递减，但笔者认为，这还是L增大的缘故。

四、自适应匹配滤波检测（Adaptive Matched Filter Test, AMF Test）

前面提到，虽然GLRT检测是基于Neyman-Person准则推导的，但由于估计值对真值的替代，事实上GLRT检测并非是一致最大功效检测（Uniformly Most Powerful Test, UMP Test），因此这也说明了存在某种检测器在某些条件下有更好的检测性能，其中一个就是AMF检测器。

一致最大功效检测（Uniformly Most Powerful Test, UMP Test）与局部最大功效检测（Locally Most Powerful Test, LMP Test）

考虑单边检测:

$H_{0}:\theta=\theta_{0},\\ H_{1}:\theta>\theta_{0}$

对于任意虚警概率 $P(H_{1}|H_{0})$ 为 $\alpha$ （某些文献也将该指标称为第一类错误概率、显著水平或概率水平）的检测器 $\varphi$ 来说，对于任意 $\theta>\theta_{0}$ 而言，如果存在一个检测器 $\varphi '$ 的正确检测概率均大于检测器 $\varphi$ ，也即：

$P_{\varphi'}(H_{1}|H_{1},\theta)>P_{\varphi}(H_{1}|H_{1},\theta)$

则检测器 $\varphi '$ 就是UMP检测，也即显著水平为 $\alpha$ 的最优检测器。需要说明的是，UMP检测器仅在单边检测中出现，且某些单边检测问题不一定存在UMP检测器[6]。

相对的，如果仅对于 $\theta_{0}$ 附近的 $\theta$ （雷达目标检测领域可理解为低信噪比目标检测）有：

$P_{\varphi'}(H_{1}|H_{1},\theta)>P_{\varphi}(H_{1}|H_{1},\theta)$

则称 $\varphi '$ 为LMP检测。

4.1 检测器推导

3.1节中GLRT检测器的推导中是先假设目标幅度b已知而先用协方差矩阵 $\mathbf{M}$ 的极大似然估计值替代似然比中的真值，而后再用b的极大似然估计值替代似然比中的真值。若交换 $\mathbf{M}$ 和b估计值的替代次序，最后就可以得到AMF检测器的检验统计量。

具体的，首先假设 $\mathbf{M}$ 已知，得到b的极大似然估计：

$\widehat{b}=\frac{\mathbf{s}^{H}\mathbf{M}^{-1}\mathbf{z}}{\mathbf{s}^{H}\mathbf{M}^{-1}\mathbf{s}}$

将 $\widehat{b}$ 带入到3.1的似然比中并作以简化得到检验统计量：

$l=\frac{|\mathbf{s}^{H}\mathbf{M}^{-1}\mathbf{z}|^{2}}{\mathbf{s}^{H}\mathbf{M}^{-1}\mathbf{s}}$

之后利用次要数据得到 $\mathbf{M}$ 的极大似然估计：

$\widehat{\mathbf{M}}=\frac{1}{K}\sum_{k=1}^{K}z(k)z(k)^{H}$

将上式代入 $l$ 中可得到最终的AMF的检验统计量[3]：

$l_{\rm AMF}=\frac{|\mathbf{s}^{H}\widehat{\mathbf{M}}^{-1}\mathbf{z}|^{2}}{\mathbf{s}^{H}\widehat{\mathbf{M}}^{-1}\mathbf{s}}$

对比 $l_{\rm AMF}$ 与3.1节中GLRT的检验统计量 $\eta$ 可知， $l_{\rm AMF}$ 的分母中省略了 $\eta$ 分母中中括号内的计算项，这大大减轻了AMF的实时计算负担。此外，当次要数据数量K非常大时，AMF检测就和GLRT检测一致了，从后面的实验结果也可以看到这一结论。

4.2 AMF检测性能参数

以上在对信号归一化相位矢量s的讨论中，笔者提到可将其建模为已知量，因为匹配滤波过程中的滤波器系数是固定已知的，此外，上面假设了滤波器系数与实际信号相位完全匹配。然而在实际滤波过程中，我们不但要考虑某些滤波器系数和信号相位矢量的正交性，也即滤波器组对信号的选择性或者说对副瓣杂波信号的抑制能力，还要考虑滤波器组的有限性带来的失配问题，也即离散效应使得与信号相位矢量最匹配的滤波器依旧存在失配，这个时候就需要考虑失配对检测器的影响。

假设信号真实的归一化相位矢量为 $\mathbf{p}$ ，滤波器系数为 $\mathbf{M}^{-1}\mathbf{q}$ ，不同于3.2节中对s做的归一化，此处对p和q的归一化为：

$\mathbf{p}^{H}\mathbf{p}=\mathbf{q}^{H}\mathbf{q}=1$

并且定义内积：

$A_{\mathbf{q}}=\mathbf{q}^{H}\mathbf{M}^{-1}\mathbf{q},\\ A_{\mathbf{p}}=\mathbf{p}^{H}\mathbf{M}^{-1}\mathbf{p}$

此时当且仅当 $\mathbf{p}=\mathbf{q}$ 时，滤波器输出最大信噪比：

${\rm SNR}_{\mathbf{pp}}=|b|^{2}A_{\mathbf{p}}$

可以看到，虽然对相位矢量的归一化不同，但输出信噪比与3.1节中定义的信噪比a一致。

当滤波器系数与信号矢量不匹配时，输出信噪比为：

$a={\rm SNR}_{\mathbf{qp}}=|b|^{2}\frac{|\mathbf{q}^{H}\mathbf{M}^{-1}\mathbf{p}|^{2}}{\mathbf{q}^{H}\mathbf{M}^{-1}\mathbf{q}}$

此时信噪比损失可表示为：

$\cos^{2}\theta=\frac{{\rm SNR}_{\mathbf{qp}}}{{\rm SNR}_{\mathbf{pp}}}=|\frac{\mathbf{q}^{H}\mathbf{M}^{-1}\mathbf{p}}{A_{\mathbf{p}}A_{\mathbf{q}}}|^{2}$

进而有：

$\cos\theta e^{j(N-1)\phi}=\frac{\mathbf{q}^{H}\mathbf{M}^{-1}\mathbf{p}}{A_{\mathbf{p}}A_{\mathbf{q}}}$

其实，如果对数字波束形成有了解，就能联想到，当 $\mathbf{M}$ 为单位阵时， $\cos\theta$ 就是空间谱函数的模值：

$\cos\theta=\frac{\sin(N\phi/2)}{N\sin(\phi/2)}$

其中 $\phi$ 表示导向矢量方向和来波方向正弦值的差值。

如果将 ${\rm SNR}_{\mathbf{qp}}$ 看作目标信号在滤波器系数 $\mathbf{M}^{-1}\mathbf{q}$ 张成的子空间内的信噪比，那么目标在 $\mathbf{M}^{-1}\mathbf{q}$ 张成的子空间的某一正交子空间内的信噪比为：

$c={\rm SNR}_{\mathbf{pp}}\sin^{2}\theta$

基于以上的建模和叙述，这里也直接给出文献[3]中的数理推导结果，首先AMF检测器最终可简化为：

$|v|^{2}\begin{matrix} H_{1}\\ >\\ <\\ H_{0} \end{matrix}\alpha\rho T$

其中 $v$ 的似然函数为：

$v\sim \left\{\begin{matrix} N(\sqrt{\rho}A_{\mathbf{p}}b\cos\theta,1) & ,H_{1}\\ N(0,1) & ,H_{0} \end{matrix}\right.$

$\rho$ 表示信噪比损失，其概率密度函数可建模为：

$f(\rho)=e^{-c\rho}\sum_{m=0}^{L+1}{\rm C}^{m}_{L+1}\frac{(N+L-1)!}{(N+L-1+m)!}c^{m}f_{\beta}(\rho;L+1,N+m-1)$

其中 $f_{\beta}$ 与3.2节中定义的beta函数一致：

$f_{\beta}(x;n,m)=\frac{(n+m-1)}{(n-1)!(m-1)!}x^{n-1}(1-x)^{m-1}$

可以看到，当滤波器不存在失配时，也即第3节中GLRT的隐含假设条件满足时有 $c=0$ ，此时信噪比损失 $\rho$ 与3.2节中信噪比损失r一致。

$\alpha$ 为用以调整门限的常数值。T为服从自由度为2L(这里依旧L=K-N+1)的卡方分布的随机变量。

依旧同3.2节中一样先假设信噪比损失 $\rho$ 为固定值，同时假设目标不起伏即b为常数，则同3.2节一样可以得到AMF检测器的条件虚警概率和条件检测概率为：

$P_{\rm FA}(\rho,c=0)=\frac{1}{(1+\alpha\rho)^{L}},\\ P_{\rm D}(\rho,b)=1-\frac{1}{(1+\alpha\rho)^{L}}\sum_{k=1}^{L}{\rm C}_{L}^{k}(\alpha\rho)^{k}S_{k}(\frac{a\rho}{1+\alpha\rho})$

对其求期望得到：

$P_{FA}=\int_{0}^{1}P_{\rm FA}(\rho,c=0){\rm d}\rho=\int_{0}^{1}\frac{f_{\beta}(\rho;L+1,N+1)}{(1+\alpha\rho)^{L}}{\rm d}\rho,\\ P_{\rm D}(b)=\int_{0}^{1}P_{\rm D}(\rho,b){\rm d}\rho$

这些性能无闭式解[3]，但可以利用其数值解进行分析。此外，根据不同的Swerling模型，还可以通过对 $P_{\rm D}(b)$ 关于b求期望得到不同模型下的检测概率。

4.3 GLRT和AMF检测性能对比

（1）不存在滤波失配情况下的检测器性能对比

当不存在滤波失配且目标不起伏时，文献[3]给出了该假设下不同参数下的匹配滤波检测器、GLRT检测器、和AMF检测器的ROC曲线对比如下：

通过以上结果图可得到如下结论：

以上参数和条件下，GLRT相对于AMF的信噪比增益不足1dB,且该增益随着信噪比的增加而减小，并且在较高信噪比处两曲线会存在交叉，也即AMF的性能好于GLRT，这也说明了GLRT并非UMP检测。
随着样本数量的增加，GLRT和AMF检测器的性能趋近，这也证实了4.1节末尾的分析。

文献[3]还给出了Swrling I起伏模型下的曲线对比图如下：

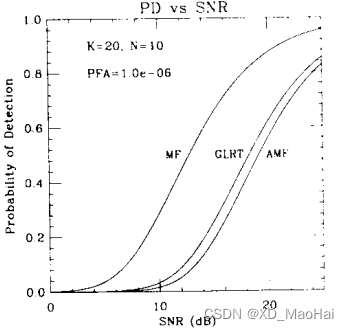
通过对比上图依旧能得到如上的两条结论，此外对比以上四幅图的匹配滤波器曲线可知，低信噪比情况下目标起伏对检测有利，高信噪比时则目标固定会更有利于检测。

（2）滤波失配情况下的检测器性能对比

文献[3]给出了滤波失配情况下（也即 $c\neq0$ ）各检测器的ROC对比图如下：

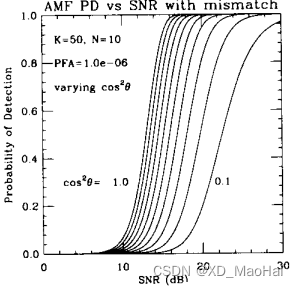
通过对比上图可知，随着失配程度的增大，GLRT检测器的性能急剧下降，AMF检测器则对失配不太敏感，这也说明了GLRT的一个优越之处：信噪比高时有较好的副瓣杂波抑制能力。

为了更好的比较AMF和GLRT的性能差异，文献[3]还给出了为达到与AMF同样的检测性能，GLRT所需额外信噪比随信噪比的变换曲线如下：

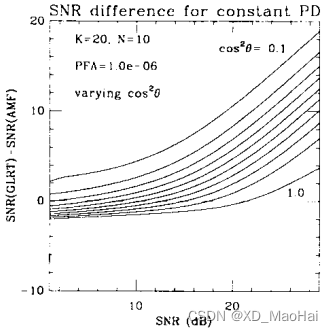
通过对比以上两图可以得到如下结论：

当滤波失配时，随着信噪比的增大GLRT相对于AMF的信噪比损失越大，这也再次说明了GLRT在高信噪比时有较好的副瓣杂波抑制能力，但是低信噪比时两者的杂波抑制能力没有很大差别。
滤波失配情况下，随着K值的增大，以上两图过纵轴原点即GLRT和AMF性能相同的信噪比点越来越小，GLRT高信噪比杂波抑制能力越来越接近AMF。

此外，为进一步具象化杂波抑制能力，文献[3]在数字波束形成的应用场景中，假设损失值 $\cos\theta$ 为 $\sin(N\phi/2)/(N\sin(\phi/2))$ (4.2节中有提到)，给出了GLRT和AMF检测器检测概率随 $\phi$ 的变化曲线如下：

我们熟知空间谱函数，进而不妨将上图理解为检测空间谱函数，为了保证较高测量精度以及较好的杂波抑制能力，我们期望空间普函数主瓣较窄，副瓣较低些。通过上图我们不难得知：

GLRT检测空间谱函数的主瓣比AMF窄，且副瓣较低，因此具有测量精度和杂波抑制能力。
信噪比越低，主瓣越窄，副瓣越低，但付出的代价是检测概率的损失。
次要数据样本量K值越大，检测概率越高，主瓣越宽，副瓣越高。

五、Wald检测和Rao检测（Wald Test and Rao Test）

Wald检测和Rao检测是两种与GLRT检测渐进相同的检测，也即当次要数据样本量K趋近无穷大时，Wald和Rao检测与GLRT检测性能趋于一致[6]，实际中用这两种检测替代GLRT检测器的一大原因就是两种检测的检验统计量计算简单。

由于篇幅限制，以下会简单的给出两种检测器的关键结果公式，具体推导可见文献[6]的Appendix 6A和6B。在给出两种检测器的表达式之前，这里先给出兴趣参数(Interest Parameters)和干扰参数(Nuisance Parameters)的概念。

兴趣参数(Interest Parameters)和干扰参数(Nuisance Parameters)

兴趣参数：衡量不同假设条件下数据关键特征的参数，在前几节的检测问题中，信号复标量幅度就是兴趣参数。

干扰参数：衡量不同假设条件下数据相同特征的参数，在前几节的检测问题中，信号杂噪背景协方差矩阵就是干扰参数。

则对于以下的假设问题而言：

$H_{0}:\mathbf{\theta}_{r}=\mathbf{\theta}_{r0},\mathbf{\theta}_{s}\\ H_{1}:\mathbf{\theta}_{r}\neq\mathbf{\theta}_{r0},\mathbf{\theta}_{s}$

其中 $\mathbf{\theta}_{r}$ 就是兴趣参数， $\mathbf{\theta}_{s}$ 就是干扰参数。

以上提到GLRT检测器是利用未知参数的极大似然估计值推导得来，我们不妨将不同假设条件下的未知参数表示成兴趣参数和干扰参数的组合列向量：

$\mathbf{\theta}_{0}=[\mathbf{\theta}_{r0}^{T},\mathbf{\theta}_{s0}^{T}]^{T},\mathbf{\theta}_{1}=[\mathbf{\theta}_{r1}^{T},\mathbf{\theta}_{s1}^{T}]^{T}$

这些参数的极大似然估计值表示为:

$\widehat{\mathbf{\theta}}_{0}=[\mathbf{\theta}_{r0}^{T},\widehat{\mathbf{\theta}}_{s0}^{T}]^{T},\mathbf{\theta}_{1}=[\widehat{\mathbf{\theta}}_{r1}^{T},\widehat{\mathbf{\theta}}_{s1}^{T}]^{T}$

5.1 检测器表达式

其实Wald检测器和Rao检测器的思路也是用近似值替代含有未知参数的似然概率密度函数。文献[6]中指出，当样本数量较大时，原本有偏的极大似然估计值 $\widehat{\mathbf{\theta}}$ 也会渐进无偏，此时该估计值 $\widehat{\mathbf{\theta}}$ 可达到Cramer-Rao下界，也即满足：

$A:\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}}=\mathbf{I}(\mathbf{\theta})(\widehat{\mathbf{\theta}}-\mathbf{\theta})$

其中 $\mathbf{I}(\mathbf{\theta})$ 表示费舍尔信息矩阵(Fisher Information Matrix)。

费舍尔信息矩阵(Fisher Information Matrix)

费舍尔信息是一种衡量观测数据携带的关于决定数据分布的参数 $\mathbf{\theta}$ 信息量的物理量，费舍尔信息越大，观测数据对 $\mathbf{\theta}$ 掌握的信息越多，参数估计约精确。

统计学中将对数似然函数的梯度称为得分函数(Score/Informant)：

$\mathbf{s}(\mathbf{\theta})=\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}}$

该物理量表示对数似然函数对参数 $\mathbf{\theta}$ 的敏感程度。则费舍尔信息矩阵就表示得分函数的协方差矩阵[7]：

$\mathbf{I}(\mathbf{\theta})=E[\mathbf{s}(\mathbf{\theta})\mathbf{s}^{H}(\mathbf{\theta})]=E[\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{*}}\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{T}}]$

当似然函数二阶可导并且满足正则化条件时：

$\mathbf{I}(\mathbf{\theta})=E[\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{*}}\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{T}}]=-E[\frac{\partial^{2} \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{*}\mathbf{\theta}^{T}}]$

若将参数矢量 $\mathbf{\theta}$ 分块成兴趣参数和干扰参数：

$\mathbf{\theta}=[\mathbf{\theta}_{r}^{T},\mathbf{\theta}_{s}^{T}]^{T}$

则可相应的对 $\mathbf{I}(\mathbf{\theta})$ 进行分块[7]：

$\mathbf{I}(\mathbf{\theta})=\begin{bmatrix} \mathbf{I}_{\mathbf{\theta}_{r},\mathbf{\theta}_{r}}(\mathbf{\theta}) & \mathbf{I}_{\mathbf{\theta}_{r},\mathbf{\theta}_{s}}(\mathbf{\theta})\\ \mathbf{I}_{\mathbf{\theta}_{s},\mathbf{\theta}_{r}}(\mathbf{\theta}) & \mathbf{I}_{\mathbf{\theta}_{s},\mathbf{\theta}_{s}}(\mathbf{\theta}) \end{bmatrix}$

其中：

$\mathbf{I}_{\mathbf{\theta}_{r},\mathbf{\theta}_{r}}(\mathbf{\theta})=E[\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{*}_{r}}\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{T}_{r}}],\\ \mathbf{I}_{\mathbf{\theta}_{r},\mathbf{\theta}_{s}}(\mathbf{\theta})=E[\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{*}_{r}}\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{T}_{s}}],\\ \mathbf{I}_{\mathbf{\theta}_{s},\mathbf{\theta}_{r}}(\mathbf{\theta})=E[\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{*}_{s}}\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{T}_{r}}],\\ \mathbf{I}_{\mathbf{\theta}_{s},\mathbf{\theta}_{s}}(\mathbf{\theta})=E[\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{*}_{s}}\frac{\partial \ln p(x;\mathbf{\theta})}{\partial \mathbf{\theta}^{T}_{s}}]$

对 $\mathbf{I}(\mathbf{\theta})$ 进行一阶泰勒展开并省略高阶项可得：

$\frac{\partial \ln p(\mathbf{x};\mathbf{\theta})}{\partial \mathbf{\theta}}=\mathbf{I}(\mathbf{\widehat{\theta}})(\widehat{\mathbf{\theta}}-\mathbf{\theta})$

对两边求积分并由初始条件可得[6]：

$B:p(\mathbf{x};\mathbf{\theta})=p(\mathbf{x};\mathbf{\widehat{\theta}})\exp[-\frac{1}{2}(\widehat{\mathbf{\theta}}-\mathbf{\theta})\mathbf{I}(\mathbf{\widehat{\theta}})(\widehat{\mathbf{\theta}}-\mathbf{\theta})]$

后续Wald和Rao检验统计量的推导就是利用公式A和B替代似然比函数中的似然概率密度函数。

（1）Wald检测器

令公式B中：

$\mathbf{\widehat{\theta}}=\mathbf{\widehat{\theta}}_{1},{\theta}=\theta_{0}$

并代入到似然比公式中并化简得Wald检验统计量为[6]：

$l=(\widehat{\mathbf{\theta}_{1}}-\mathbf{\theta}_{0})\mathbf{I}(\mathbf{\widehat{\theta}}_{1})(\widehat{\mathbf{\theta}_{1}}-\mathbf{\theta}_{0})$

其中 $\widehat{\mathbf{\theta}_{1}}$ 表示 $H_{1}$ 条件假设下未知参数的极大似然估计值。采用兴趣参数和干扰参数的形式分块表示Wald检验统计量[7]：

$l_{\rm Wald}=(\widehat{\mathbf{\theta}}_{r1}-\mathbf{\theta}_{r0})\{[\mathbf{I}^{-1}(\mathbf{\widehat{\theta}}_{1})]_{\mathbf{\theta}_{r},\mathbf{\theta}_{r}}\}^{-1}(\widehat{\mathbf{\theta}}_{r1}-\mathbf{\theta}_{r0})$

其中 $\{[\mathbf{I}^{-1}(\mathbf{\widehat{\theta}}_{1})]_{\mathbf{\theta}_{r},\mathbf{\theta}_{r}}\}^{-1}$ 是关于 $\mathbf{I}_{\mathbf{\theta}_{s},\mathbf{\theta}_{s}}$ 的舒尔补(Schur complement)：

$\mathbf{I}_{\mathbf{\theta}_{s},\mathbf{\theta}_{s}}=(\mathbf{I}_{\mathbf{\theta}_{r},\mathbf{\theta}_{r}}-\mathbf{I}_{\mathbf{\theta}_{r},\mathbf{\theta}_{s}}\mathbf{I}_{\mathbf{\theta}_{s},\mathbf{\theta}_{s}}^{-1}\mathbf{I}_{\mathbf{\theta}_{s},\mathbf{\theta}_{r}})|_{\mathbf{\theta}=\widehat{\mathbf{\theta}}_{1}}$

依旧采用3.1节中采用的信号模型和数理符号，通过以上步骤可得到该模型下的Wald检测器为[8]：

$l_{\rm Wald}=\frac{|\mathbf{s}^{H}\mathbf{S}^{-1}\mathbf{z}|^2}{\mathbf{s}^{H}\mathbf{S}^{-1}\mathbf{s}}\begin{matrix} H_{1}\\ >\\ <\\ H_{0} \end{matrix}\gamma$

可以看到，Wald检测器与第四节中AMF检测器一致（因为 $\mathbf{S}$ 和 $\mathbf{\widehat{M}}$ 只有一个常数K的差距），也即在复高斯杂噪背景下Wald检测器与AMF检测器性能参数一致。

（2）Rao检测器

利用公式A和B并作参数替换，之后带入到似然比函数中并作化简可以得到Rao检验统计量[6]：

$l_{\rm Rao}=\frac{\partial \ln p(\mathbf{x};\mathbf{\theta})}{\partial \mathbf{\theta}}|_{\mathbf{\theta}=\mathbf{\theta}_{0}}^{T}\mathbf{I}^{-1}(\mathbf{\theta}_{0})\frac{\partial \ln p(\mathbf{x};\mathbf{\theta})}{\partial \mathbf{\theta}}|_{\mathbf{\theta}=\mathbf{\theta}_{0}}^{T}$

采用兴趣参数和干扰参数的形式分块表示Rao检验统计量[7]：

$l_{\rm Rao}=\frac{\partial \ln p(\mathbf{x};\mathbf{\theta})}{\partial \mathbf{\theta}_{r}}|_{\mathbf{\theta}=\widehat{\mathbf{\theta}}_{0}}^{T}[\mathbf{I}^{-1}(\widehat{\mathbf{\theta}}_{0})]_{\mathbf{\theta}_{r},\mathbf{\theta}_{r}}\frac{\partial \ln p(\mathbf{x};\mathbf{\theta})}{\partial \mathbf{\theta}_{r}^{*}}|_{\mathbf{\theta}=\mathbf{\widehat{\theta}}_{0}}^{T}$

同样在3.1节中采用的信号模型和数理符号下，通过上式可得Rao检测器形式为[9]：

$l_{\rm Rao}=\frac{|\mathbf{s}^{H}(\mathbf{zz}^{H}+\mathbf{S})^{-1}\mathbf{z}|^2}{\mathbf{s}^{H}(\mathbf{zz}^{H}+\mathbf{S})^{-1}\mathbf{s}}\begin{matrix} H_{1}\\ >\\ <\\ H_{0} \end{matrix}\gamma$

对比Wald(AMF)检测器可知，Rao检测器中是利用所有数据对杂噪协方差矩阵进行了估计，而Wald(AMF)则仅利用了次要数据矩阵，从此处就可以预测，为了减少待检测数据对协方差矩阵估计的影响，需要大量的次要数据进行稀释，也就是说，当次要样本数据较少时，Rao检测器的性能损失（尤其在高信噪比时）会比较大，后续的实验结果也会验证这一点。

5.2 Wald和Rao检测性能参数

5.1节中已经提到Wald检测与AMF检测器一致，因此其性能参数可参4.2节。

Rao检测器性能参数推导较为繁琐，具体可参文献[9]，这里只给出Rao检测器虚警概率为：

$P_{\rm FA}=(1-\gamma)^{K}$

可见Rao检测器依旧符合CFAR特性。

5.3 GLRT、AMF和Rao检测性能对比

（1）不存在滤波失配情况下的检测器性能对比

文献[9]给出了不存在滤波失配，目标固定不起浮情况下各种检测器的ROC曲线如下：

我们只关注图中的Rao test，AMF和GLRT曲线，可得如下结论：

次要样本数据量K越大，Rao检测的性能越好，且约接近GLRT性能。
低信噪比时Rao检测性能比AMF(Wald)检测性能优越，且样本少时比较明显，笔者认为这是低信噪比时，待检测数据和次要数据功率不会差太多，而Rao运用了所有样本进行参数估计，因此性能优于AMF检测。
高信噪比时，Rao检测与GLRT和AMF的性能差距增大，这是待检测数据污染了协方差矩阵的估计。

（2）滤波失配情况下的检测器性能对比

为了探究Rao检测的杂波抑制能力，文献[9]也给出了同4.2节中失配损失一样的定义，并比较了当虚警概率固定时，在不同失配损失下为达到一定检测概率所需的信噪比值曲线，如下：

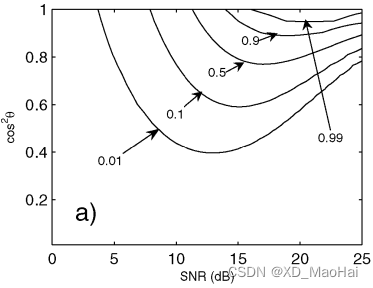
以上两幅图又称为mesa图，当曲线在纵轴分布较宽时，说明在不同损失程度下为达到检测概率不需要太大的信噪比，但这种性质带来的缺点就是量测不精确，杂波抑制能力弱。相反的，如果曲线在纵轴分布较窄时，说明检测器对失配较为敏感，对杂波抑制能力强，但缺点是需要搜索的时间较长。

以上两图中 $P_{\rm FA}=10^{-4},N=5,K=25$ 。可以看出，对于强杂波而言，需要在失配程度较小时才能达到一定的检测概率，这也就说明了Rao检测对于强杂波的抑制能力优于GLRT。

参考文献

[1] Kelly, E.J. Finite-sum expressions for signal detection probabilities. Technical Report 566, Lincoln Laboratory, M.I.T., May 20, 1981.

[2] Richards M A .Fundamentals of Radar Signal Processing, Second Edition[M]. 2005.

[3] Robey, F. C , et al. A CFAR adaptive matched filter detector. IEEE Transactions on Aerospace and Electronic Systems 28.1(1992):208-216.

[4] Reed, I.S., Mallett, J.D., and Brennan, L.E. (1974) Rapid convergence rate in adaptive arrays. IEEE Transactions on Aerospace and Electronic Systems, AES-10 (Nov. 1974), 853-863.

[5] E.J. Kelly. An adaptive detection algorithm, IEEE Transactions on Aerospace and Electronic Systems AES 22 (1) (1986) 115–127.

[6] S.M. Kay, Fundamentals of Statistical Signal Processing: DetectionTheory, Prentice-Hall, Englewood Cliffs, N, 1998.

[7] Liu W , Wang Y , Xie W. Fisher information matrix, Rao test, and Wald test for complex-valued signals and their applications[J]. Signal Processing, 2014, 94: 1-5.

[8] A. De Maio, A new derivation of the adaptive matched filter, IEEE Signal Processing Letters 11 (10) (2004) 792-793.

[9] A.De Maio, Rao test for adaptive detection in gaussian interferencewith unknown covariance matrix, IEEE Transactions on SignalProcessing 55(7)(2007) 3577-3584.

XD_MaoHai

关注

26
点赞
踩
45

收藏

觉得还不错? 一键收藏
打赏
3
评论
自适应信号检测——GLRT, AMF, Rao test, Wald test的解析和对比

本文对自适应信号处理领域中的广义似然比检测（Generalized Likelihood Ratio Test, GLRT），自适应匹配滤波检测（Adaptive Matched Filter Test, AMF Test）,Wald和Rao检测进行了学习总结，并给出了性能对比分析。
复制链接

扫一扫