强化学习丨蒙特卡洛方法及关于“二十一点”游戏的编程仿真

最新推荐文章于 2024-04-19 10:57:44 发布

XD_MaoHai

最新推荐文章于 2024-04-19 10:57:44 发布

阅读量7.5k

点赞数 13

分类专栏：强化学习文章标签：算法 python 马尔可夫链蒙特卡洛方法

本文链接：https://blog.csdn.net/qq_56937808/article/details/121136066

版权

强化学习专栏收录该内容

6 篇文章 11 订阅

订阅专栏

3.1 基于试探性出发的蒙特卡洛（蒙特卡洛ES）

3.1.1 算法介绍

3.1.2 算法应用

3.2 同轨策略（on-policy）MC控制算法

一、蒙特卡洛方法简介

在上一篇文章中，笔者介绍了动态规划算法（Dynamic Programming）的概念和实现，不难发现，动态规划是基于贝尔曼方程提出的一种迭代解法，即利用策略评估迭代计算价值，利用策略改进让智能体进行策略学习，但该算法需要完备的环境知识，即动态函数 $p(s^{'},r|s,a)$ ，另一方面，动态规划算法的迭代过程是自举的过程，即当前价值估计需要基于其他价值的估计。

假设智能体处在一个未知的环境中（其实现实生活中这种环境占大多数），环境的动作收益和状态转移都不能提前预知，这时智能体就需要仅从与环境交互的经验中做出决策，即通过平均样本的回报来解决强化学习问题，同时各个价值的估计互不影响，不具有自举特性，这就是蒙特卡洛方法（Monte Carlo method，MC），运用该算法的一个典型例子就是利用随机点占比来计算 $\pi$ 值，另一个例子就是计算积分，这两个例子比较简单常见，由于篇幅有限这里就不赘述了。

另外，之前笔者也有写过关于多臂老虎机的文章：强化学习丨多臂老虎机相关算法的总结及其MATLAB仿真https://blog.csdn.net/qq_56937808/article/details/120473326?spm=1001.2014.3001.5501https://blog.csdn.net/qq_56937808/article/details/120473326?spm=1001.2014.3001.5501

其实多臂老虎机的问题也是在没有环境的先验知识下，基于平均每个动作的收益来进行决策的，但其与蒙特卡洛方法的区别在于，蒙特卡洛算法对应多个状态，每个状态都是单独的老虎机问题，类似于上下文相关的老虎机，并且这些老虎机是相互关联的。虽有此区别，但在价值函数的估计上蒙特卡洛方法可沿用多臂老虎机的诸多方法（如UCB，ε-贪心算法）。

此外，为了保证得到有良好定义的回报，本篇文章我们只定义用于分幕式人物的蒙特卡洛算法。

二、蒙特卡洛预测

2.1 算法介绍

对于解决有限马尔科夫决策问题，最先考虑的应是一个策略对应的价值预测，即策略评估，了解过多臂老虎机问题的朋友应该不难想到，一个显而易见的方法就是根据经验进行估计，即对该状态后的回报进行平均，随着观测的次数逐渐增多，平均值就会收敛到期望值，这就是蒙特卡洛预测算法的基本思路。

在给定的一幕中，每次状态s出现都成为对其的一次访问，而对于回报的平均有两种访问方法，一种是首次访问，另一种是每次访问。首次访问是利用每幕中第一次对s访问的回报的平均值进行价值估计，而每次访问则是对s所有访问的回报的平均值进行价值估计。

两者虽访问方式不同，但当s的访问次数趋向于无穷时，两种方法下的价值估计都会收敛到正确值 $v_{\pi}(s)$ 。两者不同之处在于，对于首次访问而言，算法的每个回报都是对 $v_{\pi}(s)$ 的一个独立同分布估计，且估计方差有限，且每次平均都是无偏估计，误差的标准差也会随访问次数的增多而慢慢衰减。而在每次访问型中，估计值会二阶收敛到 $v_{\pi}(s)$ 。但在采样样本较少时，为拓展样本量可选用每次访问。以下给出首次访问型MC预测算法流程：

首次访问型MC预测算法

Step1：输入待评估的策略 $\pi$

Step2：初始化状态价值函数 $V(s)$ 、状态回报 $Returns(s)$ 为零向量

Step3：根据需要幕数量进行循环：

根据 $\pi$ 生成一幕序列： $S_{0},A_{0},R_{1},S_{1},A_{1},R_{2},\cdots ,S_{T-1},A_{T-1},R_{T}$

初始化回报 $G=0$

对本幕中的每一步进行倒叙循环,即 $t=T-1,T-2,\cdots,0:$

   $G=\gamma G+R_{t+1}$

若 $S_{t}$ 在 $S_{0},S_{1},\cdots,S_{t-1}$ 中已经出现过：

$continue$

否则：

           $Returns(S_{t})=Returns(S_{t})+G$

   $V(S_{t})=average(Returns(S_{t}))$

若将上述算法流程中的“ 若 $S_{t}$ 在 $S_{0},S_{1},\cdots,S_{t-1}$ 中已经出现过”的判断条件删去而无条件进行下面的回报平均，算法就成为了每次访问型MC预测算法。

2.2 二十一点（Blackjack）

二十一点游戏是蒙特卡洛算法的一个经典问题，接下来本篇文章都会基于此问题来对算法进行实例应用与编程仿真，先给出该游戏规则的介绍：

二十一点（Blackjack）

二十一点游戏是一种卡牌游戏，其目标是使得玩家的牌点数总和在不大于21点的情况下越大越好。所有的人头牌（J,Q,K）的点数为10，A除可用过1点外，在牌点数总和不超过21点的情况下也可以看作为11，并把A叫做“可用A”，若只能当作1就叫做“无可用A”。

游戏开始时会给玩家（Player）和庄家（Dealer）各发两张牌，庄家的牌一张正面朝上，一张背面朝上，若此时玩家的两张牌总和为21则称为天和，除非庄家也是天和，否则玩家直接获胜。之后玩家先根据需要选择是否一张一张的要牌，直到他主动停止要牌（停牌）或是牌总点数大于21（爆牌），若玩家爆牌则直接输掉游戏，否则轮到庄家行动，庄家会根据一个固定的策略进行游戏，假设庄家策略为一直要牌，直到点数等于或超过17时停牌，若庄家爆牌，则玩家获胜，否则谁的牌总点数大谁就获胜。获胜者得到+1的收益，失败者获得-1的收益，平局则均获得0的收益。

若将每局游戏看为一幕（episode），则每次玩家决策时的考量则是自己手牌的总和（12~21），庄家显示的牌（A~10），以及是否有可用A，其中，由于每次要的牌最大不会超过10，即在点数小于11时玩家都会要牌，因此可将玩家手牌的总和区间简化为[12,21]。这样一来，玩家决策的考量依据就可以看作玩家的状态，不难计算玩家的状态数为200。

又由于该游戏中玩家动作有限，即要牌和停牌，且收益仅为-1、+1与0，二十一点游戏是一个典型的分幕式有限马尔可夫决策过程。虽然可根据一定的概率论知识计算出动态函数构建完备的环境知识，进而利用动态规划的算法计算出价值函数，但这一过程无疑是非常困难的。例如假设玩家手牌为13，庄家名牌为2，无可用A，然后选择停牌，则决策后的下一状态和收益分布该怎么计算呢，这是一个非常复杂且易错的过程。

因此，在这种环境知识不好建立的情况下，可选择蒙特卡洛方法。我们不妨将玩家策略定为：在牌点数之和小于20时一直要牌，否则停牌，并利用蒙特卡洛预测算法对其进行价值计算。

2.3 算法应用

首先导入需要用到的库：

# Project Name: BlackJack
# Algorithm   : First visit prediction（首次访问策略评估）
# Author      : XD_MaoHai
# Reference   : Jabes

import matplotlib
import numpy as np
import gym
import sys
from collections import defaultdict
from matplotlib import pyplot as plt

根据算法流程编写首次访问MC预测算法函数：

# 首次访问MC预测算法
def firstvisit_prediction(policy, env, num_episodes):
    """
    policy      : 待评估策略
    env         : 问题环境
    num_episodes: 幕数量
    return      : 返回状态价值函数
    """
    # 初始化回报和
    r_sum = defaultdict(float)
    # 初始化访问次数
    r_count = defaultdict(float)
    # 初始化状态价值函数
    r_v = defaultdict(float)

    # 对各幕循环迭代
    for each_episode in range(num_episodes):
        # 输出迭代过程
        print("Episode {}/{}".format(each_episode, num_episodes), end="\r")
        sys.stdout.flush()

        # 初始化空列表记录幕过程
        episode = []
        # 初始化环境
        state = env.reset()

        # 生成（采样）幕
        done = False
        while not done:
            # 根据当前状态获得策略下的下一动作
            action = policy(state)
            # 驱动环境的物理引擎得到下一个状态、回报以及该幕是否结束标志
            next_state, reward, done, info = env.step(action)
            # 对幕进行采样并记录
            episode.append((state, action, reward))
            # 更新状态
            state = next_state

        # 对生成的单幕内进行倒序迭代更新状态价值矩阵
        G = 0
        episode_len = len(episode)
        episode.reverse()
        for seq, data in enumerate(episode):
            # 记录当前状态
            state_visit = data[0]
            # 累加计算期望回报
            G += data[2]
            # 若状态第一次出现在该幕中则更新状态价值
            if seq != episode_len - 1:
                if data[0] in episode[seq+1:][0]:
                    continue
            r_sum[state_visit] += G
            r_count[state_visit] += 1
            r_v[state_visit] = r_sum[state_visit] / r_count[state_visit]
    return r_v

定义玩家策略：

# 玩家策略
def player_policy(state):
    """
    state : 当前状态
    return: 返回当前状态下的采取动作
    """
    player_score, _, _ = state
    return 0 if player_score >= 20 else 1

绘制状态价值函数三维图像需生成三维数据：

# 处理价值矩阵方便后续绘图
def process_data_for_draw(v, ace):
    """
    v     : 状态价值函数
    ace   : 是否有可用A
    return: 返回处理好的三个坐标轴
    """

    # 生成网格点
    x_range = np.arange(12, 22)
    y_range = np.arange(1, 11)
    X, Y = np.meshgrid(x_range, y_range)

    # 根据是否有可用的A选择绘制不同的3D图
    if ace:
        Z = np.apply_along_axis(lambda _: v[(_[0], _[1], True)], 2, np.dstack([X, Y]))
    else:
        Z = np.apply_along_axis(lambda _: v[(_[0], _[1], False)], 2, np.dstack([X, Y]))
    return X, Y, Z

编写三维画图函数：

# 编写三维画图函数
def plot_3D(X, Y, Z, xlabel, ylabel, zlabel, title):
    fig = plt.figure(figsize=(20, 10), facecolor = "white")
    ax = fig.add_subplot(111, projection = "3d")
    surf = ax.plot_surface(X, Y, Z, rstride = 1, cstride = 1,
    cmap = matplotlib.cm.rainbow, vmin=-1.0, vmax=1.0)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    ax.set_zlabel(zlabel)
    ax.set_title(title)
    ax.view_init(ax.elev, -120)
    ax.set_facecolor("white")
    fig.colorbar(surf)
    return fig

编写主函数：

# 主函数
if __name__ == '__main__':
    # 从gym库中调用Blackjack-v1环境
    env = gym.make("Blackjack-v1")
    # 对策略进行评估（预测）
    v = firstvisit_prediction(player_policy, env, num_episodes=1000000)
    print(v)
    # 3D绘图
    X, Y, Z = process_data_for_draw(v, ace=True)
    fig = plot_3D(X, Y, Z, xlabel="Player Sum", ylabel="Dealer Open Card", zlabel="Value", title="Usable Ace")
    fig.show()
    fig.savefig("./result_picture/Usable_Ace.jpg")
    X, Y, Z = process_data_for_draw(v, ace=False)
    fig = plot_3D(X, Y, Z, xlabel="Player Sum", ylabel="Dealer Open Card", zlabel="Value", title="No Usable Ace")
    fig.show()
    fig.savefig("./result_picture/NO_Usable_Ace.jpg")

在引入的库中，gym库是构造强化学习环境的专用库，其中包含了包括二十一点游戏在内的诸多游戏环境，想具体学习该库及其函数的用法的朋友可参以下链接，由于篇幅有限这里就不班门弄斧了：

会飞的小鸡：强化学习之Gym基础入门(1)https://blog.csdn.net/woshi_caibi/article/details/82344436https://blog.csdn.net/woshi_caibi/article/details/82344436

此外需要注意的是，为了简化程序，文中多次用到了defaultdict函数来构建字典，而不是利用普通的dict函数并逐个遍历状态初始化，这样一来当字典里的key不存在但被查找时，返回的不是keyError而是返回一个和括号里同一类型的默认值，如int对应整数0，float对应浮点数0。

运行程序，学习1000000幕后得到有可用A与无可用A两种情况下的状态函数三维图如下：

将以下代码注释掉，原程序即成为每次访问型算法：

# # 若状态第一次出现在该幕中则更新状态价值
            # if seq != episode_len - 1:
            #     if data[0] in episode[seq+1:][0]:
            #         continue

同样得到结果图如下：

可见两种访问形式下得到的预测结果均收敛且基本一致。

三、蒙特卡洛控制

在明白如何进行策略价值预测即策略评估后，就需要考虑如何基于估计的价值来对策略进行改进，在动态规划算法中就运用了这种策略评估和策略改进相互作用的广义策略迭代思想，其策略改进的方法就是贪心的选择该状态下动作价值函数最高的动作，由于环境知识完备，这种选择方法可以基于评估好的状态价值函数，如下：

但是对于一个未知环境，如果仅得到评估好的状态价值函数，由于不知道动态函数，就无法计算得到在状态s下采取哪个动作会得到最高的期望回报，因此在这种情况下就需要对动作的价值 $Q_{\pi}(s,a)$ 进行评估，这样一来，在利用MC预测算法得到的动作价值函数基础上，贪心的选择某状态对应的最大动作价值的动作，如下：

$\pi(S_{t})=\underset{a}{argmax}\ Q_{\pi}(S_{t},a)$

这样不断的利用MC算法进行策略评估和策略改进的过程就是蒙特卡洛控制（MC控制）。

但是这个算法存在的一个问题就是，因为贪心的选择，被访问过的状态的动作会固定，这样一来其他动作的价值就会得不到预测，智能体就无法学习其他动作，因此最后的策略会局部最优，而非全局最优。这个问题仍是多臂老虎机所提到的开发与试探之间的矛盾所产生的，因此为解决开发（贪心）带来的负面效果，就需要加大试探力度，在本问题中就是如何获得贪心动作之外的其他动作样本，这就是后面几个算法要讨论的问题核心。

3.1 基于试探性出发的蒙特卡洛（蒙特卡洛ES）

3.1.1 算法介绍

很容易想到的一个获取贪心动作之外的其他动作样本的方法就是，在每幕的开始随机生成状态 $S_0$ 和动作 $A_0$ ，然后从此出发以策略 $\pi$ 生成一幕序列，这样就在幕的开始采样到了贪心动作外的其他动作，之后根据生成的幕进行策略评估和改进即得到基于试探性出发的蒙特卡洛算法，其首次访问型算法流程如下：

基于试探性出发的蒙特卡洛（蒙特卡洛ES）（首次访问型）

Step1：任意初始化策略 $\pi(s)\in A(s)$

             初始化状态价值函数 $Q(s,a)$ 、动作回报 $Returns(s,a)$ 为零向量

Step2：根据需要幕数量进行循环：

基于状态和动作空间随机生成状态 $S_0$ 和动作 $A_0$

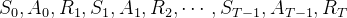
                      之后以策略 $\pi$ 生成一幕序列： $S_{0},A_{0},R_{1},S_{1},A_{1},R_{2},\cdots ,S_{T-1},A_{T-1},R_{T}$

                      初始化回报 $G=0$

对本幕中的每一步进行倒叙循环,即 $t=T-1,T-2,\cdots,0:$

   $G=\gamma G+R_{t+1}$

若 $S_{t}$ 在 $S_{0},S_{1},\cdots,S_{t-1}$ 中已经出现过：

$continue$

否则：

   $Returns(S_{t},A_{t})=Returns(S_{t},A_{t})+G$

   $Q(S_{t},A_{t})=average(Returns(S_{t},A_{t}))$

   $\pi(S_{t})=\underset{a}{argmax}\ Q_{\pi}(S_{t},a)$

注意到这里有平均的计算，这里可以用增量式实现来代替求和再求平均，如下：

$Q_{n+1}(S_{t},a)=Q_{n}(S_{t},a)+\frac{1}{n}(G-Q_{n}(S_{t},a))$

其中n是某状态-动作二元组首次访问的次数。

3.1.2 算法应用

根据上述算法流程针对二十一点问题进行编程，现给出整个代码文件如下：

# Project Name: BlackJack
# Algorithm   : MCES(基于试探性出发的蒙特卡洛)
# Author      : XD_MaoHai
# Reference   : Jabes


import matplotlib
import numpy as np
import gym
import sys
import random
from collections import defaultdict
from matplotlib import pyplot as plt
import seaborn as sns


# 编写三维画图函数
def plot_3D(X, Y, Z, xlabel, ylabel, zlabel, title):
    fig = plt.figure(figsize=(20, 10), facecolor = "white")
    ax = fig.add_subplot(111, projection = "3d")
    surf = ax.plot_surface(X, Y, Z, rstride = 1, cstride = 1,
    cmap = matplotlib.cm.rainbow, vmin=-1.0, vmax=1.0)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    ax.set_zlabel(zlabel)
    ax.set_title(title)
    ax.view_init(ax.elev, -120)
    ax.set_facecolor("white")
    fig.colorbar(surf)
    return fig


# 首次访问MC预测算法
def MCES(env, num_episodes):
    """
    env         : 问题环境
    num_episodes: 幕数量
    return      : 返回状态价值函数与最优策略
    """

    # 初始化策略(任何状态下都不要牌)
    policy = defaultdict(int)
    # 初始化回报和
    r_sum = defaultdict(float)
    # 初始化访问次数
    r_count = defaultdict(float)
    # 初始化状态价值函数
    r_v = defaultdict(float)

    # 对各幕循环迭代
    for each_episode in range(num_episodes):
        # 输出迭代过程
        print("Episode {}/{}".format(each_episode, num_episodes), end="\r")
        sys.stdout.flush()

        # 初始化空列表记录幕过程
        episode = []
        # 初始化环境
        state = env.reset()
        # 选择试探性的初始状态动作
        action = random.randint(0, 1)

        # 生成（采样）幕
        done = False
        while not done:
            # 驱动环境的物理引擎得到下一个状态、回报以及该幕是否结束标志
            next_state, reward, done, info = env.step(action)
            # 对幕进行采样并记录
            episode.append((state, action, reward))
            # 更新状态
            state = next_state
            # 根据当前状态获得策略下的下一动作
            action = policy[state]

        # 对生成的单幕内进行倒序迭代更新状态价值矩阵
        G = 0
        episode_len = len(episode)
        episode.reverse()
        for seq, data in enumerate(episode):
            # 记录当前状态
            state_visit = data[0]
            action = data[1]
            # 累加计算期望回报
            G += data[2]
            # 若状态第一次出现在该幕中则进行价值和策略更新
            if seq != episode_len - 1:
                if data[0] in episode[seq+1:][0]:
                    continue
            r_sum[(state_visit, action)] += G
            r_count[(state_visit, action)] += 1
            r_v[(state_visit, action)] = r_sum[(state_visit, action)] / r_count[(state_visit, action)]
            if r_v[(state_visit, action)] < r_v[(state_visit, 1-action)]:
                policy[state_visit] = 1 - action
    return policy, r_v


# 处理价值矩阵方便后续绘图
def process_q_for_draw(q, policy, ace):
    """
    v     : 状态价值函数
    ace   : 是否有可用A
    return: 返回处理好的三个坐标轴
    """
    # 根据动作价值函数到处最优状态价值函数
    v = defaultdict(float)
    for state in policy.keys():
        v[state] = q[(state, policy[state])]
    # 生成网格点
    x_range = np.arange(12, 22)
    y_range = np.arange(1, 11)
    X, Y = np.meshgrid(x_range, y_range)

    # 根据是否有可用的A选择绘制不同的3D图
    if ace:
        Z = np.apply_along_axis(lambda _: v[(_[0], _[1], True)], 2, np.dstack([X, Y]))
    else:
        Z = np.apply_along_axis(lambda _: v[(_[0], _[1], False)], 2, np.dstack([X, Y]))
    return X, Y, Z


# 处理策略方便后续绘图
def process_policy_for_draw(policy, ace):
    """
    policy:输入策略
    ace   :是否有可用A
    return:以二维数组形式返回
    """
    policy_list = np.zeros((10, 10))
    # 将字典形式换为列表，方便后续作图
    if ace:
        for playerscores in range(12, 22):
            for dealercard in range(1, 11):
                policy_list[playerscores - 12][dealercard - 1] = policy[(playerscores, dealercard, 1)]
    else:
        for playerscores in range(12, 22):
            for dealercard in range(1, 11):
                policy_list[playerscores - 12][dealercard - 1] = policy[(playerscores, dealercard, 0)]
    return policy_list


# 主函数
if __name__ == '__main__':
    # 从gym库中调用Blackjack-v1环境
    env = gym.make("Blackjack-v1")
    # 对策略进行评估（预测）
    policy, q = MCES(env, num_episodes=5000000)
    print(policy)
    # 绘制最优策略矩阵热力图
    # 准备画布大小，并准备多个子图
    _, axes = plt.subplots(1, 2, figsize=(40, 20))
    # 调整子图的间距，wspace=0.1为水平间距，hspace=0.2为垂直间距
    plt.subplots_adjust(wspace=0.1, hspace=0.2)
    # 这里将子图形成一个1*2的列表
    axes = axes.flatten()
    # 有可用ACE下的最优策略
    fig = sns.heatmap(np.flipud(process_policy_for_draw(policy, 1)), cmap="Wistia", ax=axes[0])
    fig.set_ylabel('Player Sum', fontsize=20)
    fig.set_yticks(list(reversed(range(10))))
    fig.set_xlabel('Dealer Open Card', fontsize=20)
    fig.set_xticks(range(10))
    fig.set_title('Usable Ace', fontsize=20)
    # 无可用ACE下的最优策略
    fig = sns.heatmap(np.flipud(process_policy_for_draw(policy, 0)), cmap="Wistia", ax=axes[-1])
    fig.set_ylabel('Player Sum', fontsize=20)
    fig.set_yticks(list(reversed(range(10))))
    fig.set_xlabel('Dealer Open Card', fontsize=20)
    fig.set_xticks(range(10))
    fig.set_title('NO Usable Ace', fontsize=20)
    plt.show()
    plt.savefig("./result_picture/MCES/Optimal Policy.jpg")

    # 3D绘图-状态价值矩阵
    X, Y, Z = process_q_for_draw(q, policy, ace=True)
    fig = plot_3D(X, Y, Z, xlabel="Player Sum", ylabel="Dealer Open Card", zlabel="Value", title="Usable Ace")
    fig.show()
    fig.savefig("./result_picture/MCES/Usable_Ace.jpg")
    X, Y, Z = process_q_for_draw(q, policy,  ace=False)
    fig = plot_3D(X, Y, Z, xlabel="Player Sum", ylabel="Dealer Open Card", zlabel="Value", title="No Usable Ace")
    fig.show()
    fig.savefig("./result_picture/MCES/NO_Usable_Ace.jpg")

运行程序，学习5000000幕后得到有可用A与无可用A两种情况下的最优策略如下：

其中横轴为庄家明的牌（从左到右为A~10），纵轴为玩家当前牌点数之和（从下到上为12~21），橙色部分动作为要牌，绿色部分动作为停牌。运行出来的结果图和Richard S.Sutton,Andrew G.Barto所著《强化学习》给出的最优策略一致。

运行程序后同样可得到最优策略下的状态价值函数三维图：

由于最优策略为固定动作，因此最优策略下的状态价值函数与动作价值函数一致，且比上一部分普通策略相应状态的价值要高，可见MCES算法起到了改进策略的作用。

3.2 同轨策略（on-policy）MC控制算法

3.2.1 算法介绍

虽然基于试探性出发的MC控制算法有时非常有效，但是也并非总是那么可靠，特别是当直接从真实环境中进行学习时，我们就很难保证试探性出发的随机性。

其实，除在幕的开始以试探的方式随机选取初始状态和动作外，还可以在幕的每一步都有试探的几率，这种方法在多臂老虎机中体现为ε-贪心算法，而在MC控制算法中则称作ε-软性策略。

在MC控制算法中，被改进的策略称为目标策略（target policy），用于生成幕序列的策略称为行为策略（behavior policy），当目标策略与行为策略一致时，将该MC算法称为同轨策略方法，否则称为离轨策略方法。

由于被改进后的策略为固定动作，再用此策略生成幕序列的话会失去试探力度，因此在同轨策略算法中，策略一般都是软性的，即在绝大多数时候都采取获得最大估计值的动作价值函数所对应的动作，但同时以一个较小的ε概率随机选择一个动作，这样一来，就会有 $\frac{\epsilon}{|A(s)|}$ 的概率选中某一非贪心动作（其中 $|A(s)|$ 表示动作数），而以 $1-\epsilon+\frac{\epsilon}{|A(s)|}$ 的概率选择贪心动作，这样的算法就是同轨策略的MC控制算法，以下给出首次访问型的算法步骤：

同轨策略的MC控制算法（首次访问型）

Step1：任意初始化一个软性策略 $\pi(s)\in A(s)$

             初始化状态价值函数 $Q(s,a)$ 、动作回报 $Returns(s,a)$ 为零向量

定义一个较小的试探概率 $\epsilon$

Step2：根据需要幕数量进行循环：

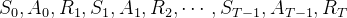
策略 $\pi$ 生成一幕序列： $S_{0},A_{0},R_{1},S_{1},A_{1},R_{2},\cdots ,S_{T-1},A_{T-1},R_{T}$

                      初始化回报 $G=0$

对本幕中的每一步进行倒叙循环,即 $t=T-1,T-2,\cdots,0:$

   $G=\gamma G+R_{t+1}$

若 $S_{t}$ 在 $S_{0},S_{1},\cdots,S_{t-1}$ 中已经出现过：

$continue$

否则：

   $Returns(S_{t},A_{t})=Returns(S_{t},A_{t})+G$

   $Q(S_{t},A_{t})=average(Returns(S_{t},A_{t}))$

   $A^{*}=\underset{a}{argmax}\ Q(S_{t},a)$

对于所有 $a\in A(S_{t})$ ：

           $\pi(a|s)=\left\{\begin{matrix} 1-\epsilon+\frac{\epsilon}{|A(s)|}&if\ a = A^{*} \\ \frac{\epsilon}{|A(s)|}& if\ a\neq A^{*} \end{matrix}\right.$

以下给出上述算法可以进行策略改进的证明：

$\begin{aligned} Q_{\pi}(s,\pi^{'}(s))&=\sum_{a}\pi^{'}(a|s)Q_{\pi}(s,a)\\ &=\frac{\epsilon}{|A(s)|}\sum_{a}Q_{\pi}(s,a)+(1-\epsilon)\underset{a}{max}\ Q_{\pi}(s,a)\\ &\geq\frac{\epsilon}{|A(s)|}\sum_{a}Q_{\pi}(s,a)+(1-\epsilon)\sum_{a}\frac{\pi(a|s)-\frac{\epsilon}{|A(s)|}}{1-\epsilon}Q_{\pi}(s,a)\\ &=\frac{\epsilon}{|A(s)|}\sum_{a}Q_{\pi}(s,a)-\frac{\epsilon}{|A(s)|}\sum_{a}Q_{\pi}(s,a)+\sum_{a}\pi(a|s)Q_{\pi}(s,a)\\ &=V_{\pi}(s) \end{aligned}$

其中 $\pi^{'}$ 表示改进后的策略， $\pi$ 表示原策略。其中的 $\geq$ 是因为右边第二项期望累加是一个和为1的非负权重进行的加权平均值，所以一定小于等于其中的最大值。通过上式可知，任何一个根据 $Q_{\pi}$ 生成的ε-贪心策略都是对其的一个改进。

3.2.2 算法应用

同轨策略的MC控制算法仅在蒙特卡洛ES代码的基础上将MCES函数换为OnPolicy函数即可，先给出该函数代码如下：

# Project Name: BlackJack
# Algorithm   : On Policy Control(同轨策略控制算法)
# Author      : XD_MaoHai
# Reference   : Jabes

……
……

# 同轨策略控制算法
def OnPolicy(env, num_episodes):
    """
    env         : 问题环境
    num_episodes: 幕数量
    return      : 返回状态价值函数与最优策略
    """
    # 试探概率
    epsilon = 0.1
    # 初始化策略(任何状态下都不要牌)
    policy = defaultdict(int)
    # 初始化回报和
    r_sum = defaultdict(float)
    # 初始化访问次数
    r_count = defaultdict(float)
    # 初始化状态价值函数
    r_v = defaultdict(float)

    # 对各幕循环迭代
    for each_episode in range(num_episodes):
        # 输出迭代过程
        print("Episode {}/{}".format(each_episode, num_episodes), end="\r")
        sys.stdout.flush()

        # 初始化空列表记录幕过程
        episode = []
        # 初始化环境
        state = env.reset()

        # 生成（采样）幕
        done = False
        while not done:
            # 根据当前状态获得策略下的下一动作
            action_list = np.random.choice([policy[state], 1-policy[state]], 1, replace=False, p=[1-epsilon/2, epsilon/2])
            action = action_list[0]
            # 驱动环境的物理引擎得到下一个状态、回报以及该幕是否结束标志
            next_state, reward, done, info = env.step(action)
            # 对幕进行采样并记录
            episode.append((state, action, reward))
            # 更新状态
            state = next_state

        # 对生成的单幕内进行倒序迭代更新状态价值矩阵
        G = 0
        episode_len = len(episode)
        episode.reverse()
        for seq, data in enumerate(episode):
            # 记录当前状态
            state_visit = data[0]
            each_action = data[1]
            # 累加计算期望回报
            G += data[2]
            # 若状态第一次出现在该幕中则进行价值和策略更新
            # if seq != episode_len - 1:
            #     if data[0] in episode[seq+1:][0]:
            #         continue
            r_sum[(state_visit, each_action)] += G
            r_count[(state_visit, each_action)] += 1
            r_v[(state_visit, each_action)] = r_sum[(state_visit, each_action)] / r_count[(state_visit, each_action)]
            # r_v[(state_visit, each_action)] = r_sum[(state_visit, each_action)] + 1/r_count[(state_visit, each_action)]*(G - r_v[(state_visit, each_action)])
            if r_v[(state_visit, each_action)] < r_v[(state_visit, 1-each_action)]:
                policy[state_visit] = 1 - each_action
    return policy, r_v
……
……

其中笔者运用了 np.random.choice函数进行概率选择。运行程序，学习5000000幕后得到有可用A与无可用A两种情况下的最优策略如下：

可见与MCES控制算法运行结果基本一致。同样得到最优策略下的状态价值函数三维图如下：

运行结果同样和MCES一致。

3.3 离轨策略（off-policy）

前面我们已经提到，MCES、同轨策略MC控制以及离轨策略MC控制等算法的提出都是为了加大试探力度以获得真实的状态-动作价值从而改进策略，MCES是仅在幕的开头试探性的随机选择状态和动作，同轨策略MC控制则是在幕的每步以一定概率尝试贪心动作外的其他动作，那我们不妨考虑下，如果生成的幕样本可以脱离目标策略，而是选择一个可以试探到任何状态-动作二元组的行为策略来生成幕样本，进而来对目标策略进行训练不就解决了试探的问题吗？而这其实就是离轨策略MC控制等算法的基本思想。

3.3.1 重要度采样

利用行为策略 $b(a|s)$ 生成的样本来训练目标策略 $\pi(s|a)$ 需要解决两个问题，其一是要求在 $\pi$ 下发生的每个动作都至少偶尔能在 $b$ 下发生，即对任意的 $\pi(s,a)>0$ ，需要有 $b(a|s)>0$ ，这一问题只需合理构建随机行为策略一般都不难做到；另一个问题是，利用行为策略产生的幕序列所得到的回报无法真实体现目标策略的实际回报，这就需要引入重要度采样（Importance Sampling）来估计目标策略的实际回报。

为了了解重要度采样，我们不妨先来考虑日常我们求积分的问题，假设被积函数为定义在[a,b]上的 $f(x)$ ，则积分公式为：

$I=\int^{b}_{a} f(x)dx$

当 $f(x)$ 的原函数不太容易求解时，我们可利用离散的思想将 $f(x)$ 分为N个宽为 $\frac{b-a}{N}$ ，高为 $f(x_{n})$ 的矩形，其中：

$x_{n}=n\cdot \frac{b-a}{N}+a,\ n=0,1,2,\cdots,N-1$

则原积分值可由下式估计：

$I=\int^{b}_{a} f(x)dx\approx \frac{b-a}{N}\sum_{n=0}^{N-1}f(x_{n})$

当上式中的N趋向于无穷时，估计值便趋向于真实积分值。

这是我们高中时就学到的一种极限思路，然而这其实就是一个利用样本来估计变量期望的一种方法，我们在中小学就学到过根据统计量计算期望的方法，那就是利用样本进行求和相加再平均，然而不知道你有没有注意到这样的题目都有一个前提，就是“随机取样”，也就是在变量的取值区间内均匀取样。

然而，如果我们不均匀取样，而是让 $x$ 依据某种非均匀分布 $p(x)$ 来进行采样，即让每个矩形的宽度不同，我们依旧能给出显式的估计积分的式子，并且合理构建 $p(x)$ 还能提高估计精度。

不难发现，计算积分时函数的较大值对积分结果影响较大，如下图：

即上图中圆形框中的部分要比矩形框中的部分对计算计算更有意义些，其实这并不难理解，比如统计一个国家的经济实力，根据经济学中的“二八定律”，就是说，社会上20%的人，占有80%的社会财富，我们则会把更多的采样力度放在这20%的人身上，这就是重要度采样的基本思想。

这样一来在样本数一样的情况下，这种非均匀采样的估算方法要比均匀采样算法好。我们不妨将上面采样策略定为 $p(x)$ ，即采样点 $x\sim p(x)$ ，则这里先直接给出估计积分的公式如下：

$I=\int^{b}_{a} f(x)dx\approx \frac{1}{N}\sum_{n=0}^{N-1}\frac{f(x_{n})}{p(x_{n})}$

这就是蒙特卡洛积分。以下给出上述式子是对积分的一种无偏估计的证明：

$E[\frac{1}{N}\sum_{n=0}^{N-1}\frac{f(x_{n})}{p(x_{n})}]=\frac{1}{N}\sum_{n=0}^{N-1}E[\frac{f(x_{n})}{p(x_{n})}]=\frac{1}{N}\sum_{n=0}^{N-1}\int_{a}^{b}p(x_{n}) \frac{f(x_{n})}{p(x_{n})}dx=\frac{1}{N}\sum_{n=0}^{N-1}\int_{a}^{b}f(x_{n}) dx$

又因为 $x_{n}$ 独立同分布，所以：

$\frac{1}{N}\sum_{n=0}^{N-1}\int_{a}^{b}f(x_{n}) dx=\int_{a}^{b}f(x_{n}) dx=I$

因此证毕。

此外，上面已经提到，合理构建 $p(x)$ 还能提高估计精度，并且 $f(x)$ 数值大的地方对估计意义较大，因此不难联想到让 $p(x)$ 在 $f(x)$ 数值大的地方也大些。事实上，从理论的角度来说，任意一个被积函数 $f(x)$ ，它的最优概率密度函数是：

$p_{op}(x)=\frac{f(x)}{\int f(x) dx}$

不过一般我们不知道 $\int f(x) dx$ 的值，因为这就是我们求解的问题，但是这对于我们构造 $p(x)$ 已经很有指导意义了，即使得 $p(x)$ 的曲线形状接近于 $f(x)$ 。

在一些求解期望的问题中，其实随机变量 $x$ 已经服从一定的分布 $p(x)$ ，则关于 $x$ 的一个函数 $f(x)$ 的期望公式为：

$E[f(x)] = \int_{a}^{b}p(x)f(x)dx$

对其进行无偏估计：

$E[f(x)] = \int_{a}^{b}p(x)f(x)dx=\frac{1}{N}\sum^{N}_{x_{n}\sim p(x),n=1}f(x)$

然而当 $p(x)$ 的形式较为复杂时采样会比较困难，此时我们可以利用一个形式较为简单或者其其CDF已知的概率密度函数 $\tilde{p}(x)$ 来进行采样，则期望公式如变为：

$E[f(x)] = \int_{a}^{b}p(x)f(x)dx=\int_{a}^{b}\tilde{p}(x)\frac{p(x)}{\tilde{p}(x)}f(x)dx$

此时可将上式看作求解服从 $\tilde{p}(x)$ 分布的随机变量 $\frac{p(x)}{\tilde{p}(x)}f(x)$ 的期望，其中 $\frac{p(x)}{\tilde{p}(x)}$ 称为重要度采样比，可以看作是对改变采样分布后对所得样本 $f(x)$ 的一种修正，则期望的无偏估计为：

$\underset{x\sim \tilde{p}(x)}{E}[\frac{p(x)}{\tilde{p}(x)}f(x)]=\frac{1}{N}\sum_{x_{n}\sim \tilde{p}(x),n=1}^{N}\frac{p(x)}{\tilde{p}(x)}f(x)$

其实，不单是当随机变量原分布密度函数比较复杂时比较可以采用重要度采样，在一些问题中也可以利用该方法进行样本拓展。比如回到我们的蒙特卡洛离轨策略问题，前面已经提到，在离轨策略中，利用行为策略产生的幕序列所得到的回报无法真实体现目标策略的实际回报，其实反映的就是改变采样策略后随机变量样本需要加权修正的问题，比如给定以下用行为策略 $b$ 生成的一幕序列：

$S_{t},A_{t},R_{t+1},S_{t+1},A_{t+1},R_{t+2},\cdots,S_{T}$

该幕序列在行为策略 $b$ 下发生的概率为：

$\begin{aligned} Pr\{S_{t},A_{t},R_{t+1},S_{t+1},A_{t+1},R_{t+2},\cdots,S_{T}|b(a|s)\}\\ &=b(A_{t}|S_{t})p(S_{t+1}|S_{t},A_{t})b(A_{t+1}|S_{t+1})\cdots p(S_{T}|S_{T-1},A_{T-1})\\ &=\prod_{k=t}^{T-1}b(A_{k}|S_{k})p(S_{k+1}|S_{k},A_{k}) \end{aligned}$

同理得该幕序列在目标策略 $\pi$ 下发生的概率为：

$\begin{aligned} Pr\{S_{t},A_{t},R_{t+1},S_{t+1},A_{t+1},R_{t+2},\cdots,S_{T}|\pi(a|s)\}\\ &=\pi(A_{t}|S_{t})p(S_{t+1}|S_{t},A_{t})\pi(A_{t+1}|S_{t+1})\cdots p(S_{T}|S_{T-1},A_{T-1})\\ &=\prod_{k=t}^{T-1}\pi(A_{k}|S_{k})p(S_{k+1}|S_{k},A_{k}) \end{aligned}$

则将 $Pr\{S_{t},A_{t},R_{t+1},S_{t+1},A_{t+1},R_{t+2},\cdots,S_{T}|\pi(a|s)\}$ 视为原分布 $p(x)$ ， $Pr\{S_{t},A_{t},R_{t+1},S_{t+1},A_{t+1},R_{t+2},\cdots,S_{T}|b(a|s)\}$ 视为 $\tilde{p}(x)$ ，随机变量为：

$f(x)=G_{t}=\sum_{k=t+1}^{T}R_{k}$

则重要度采样比为：

$\rho _{t:T-1}=\frac{\prod_{k=t}^{T-1}\pi(A_{k}|S_{k})p(S_{k+1}|S_{k},A_{k})}{\prod_{k=t}^{T-1}b(A_{k}|S_{k})p(S_{k+1}|S_{k},A_{k})}=\prod_{k=t}^{T-1}\frac{\pi(A_{k}|S_{k})}{b(A_{k}|S_{k})}$

则利用重要度采样比修正后的回报 $G_{t}$ 的期望即是策略 $\pi$ 的价值函数，如下：

$E[\rho_{t:T-1}G_{t}|S_{t}=s]=v_{\pi}(s)$

策略 $\pi$ 在上述幕序列的回报的无偏估计为：

$V(s)\doteq \frac{\sum_{n=1}^{N}\rho_{t(n):T(n)-1}G_{t(n)}}{N}$

其中N表示一共状态s的首次访问次数，t(n)表示第n幕中首次访问s的时刻，T(n)表示第n幕的终止时刻。

上述估计公式又叫做普通重要度采样，虽然是无偏估计，但由于 $b$ 与 $\pi$ 相差较大时会使得 $\rho _{t:T-1}$ 较大，而分母又是有界定值，所以这种情况下估计方差会比较大。另一种估计公式如下：

$V(s)\doteq \frac{\sum_{n=1}^{N}\rho_{t(n):T(n)-1}G_{t(n)}}{\sum_{n=1}^{N}\rho_{t(n):T(n)-1}}$

这种估计方法叫做加权重要度采样，由于引入了权重分母，因此其估计方差是有界的，另外这种估计方法是有偏的，但是偏差值会渐进收敛于零，我们在实际应用中也常用这种方法。

其实，如果仔细探究你会发现，利用上述的重要度采样比来整体修正回报值也是一种粗糙的方式，这会带来估计方差加大的负面影响，为了减小方差还可以运用折扣敏感的重要度采样以及每次决策型重要度采样方法，感兴趣的朋友可做拓展学习，这里就不赘述了（不难）。

3.3.2 离轨策略MC预测算法

上面我们已经给出了如何在离轨策略中，利用行动策略产生的样本来对目标策略进行价值估计，即利用重要度采样，那么仿照着同轨策略方法我们就不难得出离轨策略的MC预测算法。

而在给出预测算法之前，我们不妨先来观察下加权重要度采样公式，该式形式比较复杂，直接计算加权平均值的过程中需要记录诸多中间变量，我们已经知道了普通采样平均的增量式实现公式，那么我们就先来推导下加权平均的增量式实现公式：

考虑一个一般的加权平均公式：

$V_{n}\doteq \frac{\sum_{k=1}^{n-1}W_{k}G_{k}}{\sum_{k=1}^{n-1}W_{k}}$

令：

$C_{n}\doteq \sum_{k=1}^{n}W_{n}$

则原等式：

$V_{n}C_{n-1}=\sum_{k=1}^{n-1}W_{k}G_{k}$

又有：

$V_{n+1}C_{n}=\sum_{k=1}^{n}W_{k}G_{k},eq1$

$V_{n}(C_{n}-W_{n})=\sum_{k=1}^{n-1}W_{k}G_{k},eq2$

则 $eq1-eq2:$

$V_{n+1}C_{n}-V_{n}(C_{n}-W_{n})=W_{n}G_{n}$

移项合并同类项，并且方程两边同除以 $C_{n}$ 得：

$V_{n+1}=V_{n}+\frac{W_{n}}{C_{n}}(G_{n}-V_{n})$

这就是加权重要度采样的增量式实现。得到此式后不难得出离轨策略的MC预测算法流程如下：

离轨策略的MC预测算法（首次访问型）

Step1：定义目标策略 $\pi(s)$ 与行动策略 $b(s)$

             初始化状态价值函数 $Q(s,a)$ 、 $C(s,a)$ 为零向量

Step2：根据需要幕数量进行循环：

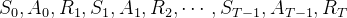
策略 $b$ 生成一幕序列： $S_{0},A_{0},R_{1},S_{1},A_{1},R_{2},\cdots ,S_{T-1},A_{T-1},R_{T}$

                      初始化回报 $G=0$ , $W=1$

对本幕中的每一步进行倒叙循环,即 $t=T-1,T-2,\cdots,0:$

   $G=\gamma G+R_{t+1}$

   $C(S_{t},A_{t})=C(S_{t},A_{t})+W$

   $Q(S_{t},A_{t})=Q(S_{t},A_{t})+\frac{W}{C(S_{t},A_{t})}[G-Q(S_{t},A_{t})]$

   $W=W\frac{\pi(A_{t}|S_{t})}{b(A_{t}|S_{t})}$

如果 $W=0$ ，则退出内层循环，进行下一幕的学习

可以看到当 $W=0$ 时，即说明我的目标策略 $\pi$ 不可能采取这样的行动，那么这个幕就没有了训练意义，即退出该幕学习。另外，你会发现 $W$ 值的更新是在 $Q$ 值的更新之后，但是按照重要度采样 $W$ 值的更新应该在 $Q$ 值的更新之前，但笔者通过仿真发现这两中顺序不影响预测结果，但其背后数学机理笔者还没搞明白，欢迎高人指点。

现给出二十一点问题的离轨策略的MC预测算法代码如下（目标策略与MC预测部分相同）：

# Project Name: BlackJack
# Algorithm   : Off Policy Prediction(离轨策略预测算法)
# Author      : XD_MaoHai
# Reference   : Jabes


import matplotlib
import numpy as np
import gym
import sys
import random
from collections import defaultdict
from matplotlib import pyplot as plt


# 编写三维画图函数
def plot_3D(X, Y, Z, xlabel, ylabel, zlabel, title):
    fig = plt.figure(figsize=(20, 10), facecolor = "white")
    ax = fig.add_subplot(111, projection = "3d")
    surf = ax.plot_surface(X, Y, Z, rstride = 1, cstride = 1,
    cmap = matplotlib.cm.rainbow, vmin=-1.0, vmax=1.0)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    ax.set_zlabel(zlabel)
    ax.set_title(title)
    ax.view_init(ax.elev, -120)
    ax.set_facecolor("white")
    fig.colorbar(surf)
    return fig

# 试探因子
epsilon = 0.1


# 行为策略
def behavior_policy(state):
    """
    state : 当前状态
    return: 返回行为策略下的采取动作
    """
    action_list = np.random.choice([target_policy(state), 1 - target_policy(state)], 1, replace=False, p=[1 - epsilon / 2, epsilon / 2])
    action = action_list[0]
    return action


# 目标策略
def target_policy(state):
    """
    state : 当前状态
    return: 返回当前状态下的采取动作
    """
    player_score, _, _ = state
    return 0 if player_score >= 20 else 1


# 离轨策略预测算法
def OffPolicy(env, num_episodes):
    """
    env         : 问题环境
    num_episodes: 幕数量
    return      : 返回状态价值函数
    """
    # 初始化重要比和
    C = defaultdict(float)
    # 初始化状态价值函数
    q = defaultdict(float)

    # 对各幕循环迭代
    for each_episode in range(num_episodes):
        # 输出迭代过程
        print("Episode {}/{}".format(each_episode+1, num_episodes), end="\r")
        sys.stdout.flush()

        # 初始化空列表记录幕过程
        episode = []
        # 初始化环境
        state = env.reset()

        # 生成（采样）幕
        done = False
        while not done:
            # 根据当前状态获得策略下的下一动作
            action = behavior_policy(state)
            # 驱动环境的物理引擎得到下一个状态、回报以及该幕是否结束标志
            next_state, reward, done, info = env.step(action)
            # 对幕进行采样并记录
            episode.append((state, action, reward))
            # 更新状态
            state = next_state

        # 对生成的单幕内进行倒序迭代更新状态价值矩阵
        G = 0
        W = 1.0
        episode_len = len(episode)
        episode.reverse()
        for seq, data in enumerate(episode):
            # 记录当前状态
            state_visit = data[0]
            each_action = data[1]
            if each_action == target_policy(state_visit):
                W = W / (1 - epsilon)
            else:
                break
            # 累加计算期望回报
            G += data[2]
            C[(state_visit, each_action)] = C[(state_visit, each_action)] + W
            # 若状态第一次出现在该幕中则进行价值和策略更新
            # if seq != episode_len - 1:
            #     if data[0] in episode[seq+1:][0]:
            #         continue
            q[(state_visit, each_action)] = q[(state_visit, each_action)] + W/C[(state_visit, each_action)]*(G - q[(state_visit, each_action)])

    return q


# 处理价值矩阵方便后续绘图
def process_q_for_draw(q, ace):
    """
    v     : 状态价值函数
    ace   : 是否有可用A
    return: 返回处理好的三个坐标轴
    """
    # 生成网格点
    x_range = np.arange(12, 22)
    y_range = np.arange(1, 11)
    X, Y = np.meshgrid(x_range, y_range)

    # 根据是否有可用的A选择绘制不同的3D图
    if ace:
        Z = np.apply_along_axis(lambda _: q[((_[0], _[1], True), target_policy((_[0], _[1], True)))], 2, np.dstack([X, Y]))
    else:
        Z = np.apply_along_axis(lambda _: q[((_[0], _[1], False), target_policy((_[0], _[1], False)))], 2, np.dstack([X, Y]))
    return X, Y, Z


# 主函数
if __name__ == '__main__':
    # 从gym库中调用Blackjack-v1环境
    env = gym.make("Blackjack-v1")
    # 对策略进行评估（预测）
    q = OffPolicy(env, num_episodes=500000)
    # 3D绘图-状态价值矩阵
    X, Y, Z = process_q_for_draw(q, ace=True)
    fig = plot_3D(X, Y, Z, xlabel="Player Sum", ylabel="Dealer Open Card", zlabel="Value", title="Usable Ace")
    fig.show()
    fig.savefig("./result_picture/OffPolicy/Prediction/Usable_Ace.jpg")
    X, Y, Z = process_q_for_draw(q, ace=False)
    fig = plot_3D(X, Y, Z, xlabel="Player Sum", ylabel="Dealer Open Card", zlabel="Value", title="No Usable Ace")
    fig.show()
    fig.savefig("./result_picture/OffPolicy/Prediction/NO_Usable_Ace.jpg")

运行程序，学习500000幕后得到状态函数三维图如下：

可见运行结果和第二部分（MC预测）结果一致。

3.3.3 离轨策略MC控制算法

能做到策略评估（预测）后，就可以利用估计好的价值函数来进行策略改进，离轨策略MC控制算法依旧用的是这种广义策略迭代思想。和同轨策略MC控制算法一致，我们依旧在策略评估后贪心的选取价值最高的动作来进行策略改进，现给出离轨策略MC控制算法流程如下：

  离轨策略的MC控制算法（首次访问型）

Step1：任意初始化一个策略 $\pi(s)\in A(s)$ ，并定义行动策略 $b(s)$

             初始化状态价值函数 $Q(s,a)$ 、 $C(s,a)$ 为零向量

Step2：根据需要幕数量进行循环：

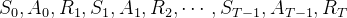
策略 $b$ 生成一幕序列： $S_{0},A_{0},R_{1},S_{1},A_{1},R_{2},\cdots ,S_{T-1},A_{T-1},R_{T}$

                      初始化回报 $G=0$ , $W=1$

对本幕中的每一步进行倒叙循环,即 $t=T-1,T-2,\cdots,0:$

   $G=\gamma G+R_{t+1}$

   $C(S_{t},A_{t})=C(S_{t},A_{t})+W$

   $Q(S_{t},A_{t})=Q(S_{t},A_{t})+\frac{W}{C(S_{t},A_{t})}[G-Q(S_{t},A_{t})]$

   $\pi(S_{t})=\underset{a}{argmax}\ Q(S_{t},a)$

如果 $A_{t}\neq \pi(S_{t})$ 则退出内层循环

   $W=W\frac{1}{b(A_{t}|S_{t})}$

注意到最后 $W$ 的更新，重要度采样比是 $\frac{1}{b(A_{t}|S_{t})}$ ，而非 $\frac{\pi(A_{t}|S_{t})}{b(A_{t}|S_{t})}$ ，这是因为策略改进是贪心的选择最优动作，若该最优动作不为采样动作则该幕样本失去学习意义即退出本幕学习，若两者一致则因为目标策略是固定的，所以 $\pi(S_{t},A_{t})$ 为1。

对于二十一点问题，利用离轨策略MC控制算法的代码就在同轨策略MC控制算法代码的基础上增加行为策略，并将OnPolicy函数换为OffPolicy即可，此两部分代码如下：

# Project Name: BlackJack
# Algorithm   : Off Policy Control(离轨策略控制算法)
# Author      : XD_MaoHai
# Reference   : Jabes

……
……
# 行为策略中每步选择1的概率
alpha = 0.5


# 行为策略
def behavior_policy(state):
    """
    state : 当前状态
    return: 返回行为策略下的采取动作
    """
    action_list = np.random.choice([1, 0], 1, replace=False, p=[alpha, 1-alpha])
    action = action_list[0]
    return action

# 离轨策略控制算法
def OffPolicy(env, num_episodes):
    """
    env         : 问题环境
    num_episodes: 幕数量
    return      : 返回状态价值函数与最优策略
    """
    # 初始化策略(任何状态下都不要牌)
    target_policy = defaultdict(int)
    # 初始化重要比和
    C = defaultdict(float)
    # 初始化状态价值函数
    q = defaultdict(float)

    # 对各幕循环迭代
    for each_episode in range(num_episodes):
        # 输出迭代过程
        print("Episode {}/{}".format(each_episode+1, num_episodes), end="\r")
        sys.stdout.flush()

        # 初始化空列表记录幕过程
        episode = []
        # 初始化环境
        state = env.reset()

        # 生成（采样）幕
        done = False
        while not done:
            # 根据当前状态获得策略下的下一动作
            action = behavior_policy(state)
            # 驱动环境的物理引擎得到下一个状态、回报以及该幕是否结束标志
            next_state, reward, done, info = env.step(action)
            # 对幕进行采样并记录
            episode.append((state, action, reward))
            # 更新状态
            state = next_state

        # 对生成的单幕内进行倒序迭代更新状态价值矩阵
        G = 0
        W = 1.0
        episode_len = len(episode)
        episode.reverse()
        for seq, data in enumerate(episode):
            # 记录当前状态
            state_visit = data[0]
            each_action = data[1]
            # 累加计算期望回报
            G += data[2]
            C[(state_visit, each_action)] = C[(state_visit, each_action)] + W
            # 若状态第一次出现在该幕中则进行价值和策略更新
            # if seq != episode_len - 1:
            #     if data[0] in episode[seq+1:][0]:
            #         continue
            q[(state_visit, each_action)] = q[(state_visit, each_action)] + W/C[(state_visit, each_action)]*(G - q[(state_visit, each_action)])
            if q[(state_visit, each_action)] < q[(state_visit, 1-each_action)]:
                target_policy[state_visit] = 1 - each_action
            if each_action == target_policy[state_visit]:
                if each_action == 1:
                    W = W / alpha
                else:
                    W = W / (1 - alpha)
            else:
                break
    return q, target_policy
……
……

运行程序，学习5000000幕后得到有可用A与无可用A两种情况下的最优策略如下：

同样得到最优策略下的状态价值函数三维图如下：

结果图均与上面结果基本一致。

XD_MaoHai

关注

13
点赞
踩
52

收藏

觉得还不错? 一键收藏
打赏
7
评论
强化学习丨蒙特卡洛方法及关于“二十一点”游戏的编程仿真

一、蒙特卡洛方法简介在上一篇文章中，笔者介绍了动态规划算法（Dynamic Programming）的概念和实现，不难发现，动态规划是基于贝尔曼方程提出的一种迭代解法，即利用策略评估迭代计算价值，利用策略改进让智能体进行策略学习，但该算法需要完备的环境知识，即动态函数，另一方面，动态规划算法的迭代过程是自举的过程，即当前价值估计需要基于其他价值的估计。假设智能体处在一个未知的环境中（其实现实生活中这种环境占大多数），环境的动作收益和状态转移都不能提前预知，这时智能体就...
复制链接

扫一扫