多站航迹相关（Track Correlation）与JPDA算法

最新推荐文章于 2024-03-11 16:56:05 发布

XD_MaoHai

最新推荐文章于 2024-03-11 16:56:05 发布

阅读量2.1k

点赞数 8

分类专栏：雷达数据处理文章标签：目标跟踪算法

本文链接：https://blog.csdn.net/qq_56937808/article/details/130467189

版权

雷达数据处理专栏收录该内容

2 篇文章 5 订阅

订阅专栏

2.4 最近邻域航迹相关算法（Nearest Neighbor，NN）

2.5 K近邻域（K-Nearest Neighbor，K-NN）与修正的K近邻域航迹相关算法（Modified K-Nearest Neighbor, MK-NN）

2.6 多义性处理

2.7 多雷达站航迹相关算法

2.8 一种K-means聚类的航迹相关算法

三、联合概率数据关联（Joint Probabilistic Data Association, JPDA）

一、引言

通过多雷达站的数据融合可获得相较于单雷达站更好的检测和跟踪性能，依据融合过程中各雷达站向融合中心传输数据形式的不同可将数据融合系统分为集中式（Centralized）系统和分布式（Distributed）系统。相较于集中式系统而言，分布式系统不需要传输庞大的回波原数据（Raw Data），而是通过传输各雷达站局部处理后的数据从而降低通信量与融合计算压力，但数据局部处理带来的信息损失也会使得其融合性能往往差于集中式系统。

对于分布式系统而言，每个雷达站均有自己的数据处理系统，同时也有独立的目标跟踪和航迹形成的能力，对各雷达站的航迹信息进行融合可以提高系统的跟踪精度，但航迹融合的前提是需要解决各雷达站的哪些航迹源于同一目标的问题，这一过程叫做相关（Correlation）。而利用关联好的多站航迹在公共坐标系上形成一条精度更高的航迹，这个过程叫做融合（Fusion）。

传统的航迹相关算法可分为基于统计的方法以及基于模糊数学的方法，本文主要对笔者最近学习的基于统计的航迹相关算法以及多目标跟踪中的联合概率数据关联（Joint Probabilistic Data Association, JPDA）算法进行梳理总结，并给出相应的推荐文献，供笔者复习和各位参考。

需要说明的是，为了区分上面的Correlation和Association，本博客中主观的将其分别翻译为相关和关联，主观的用以区分多站之间关联和单站情况下同一目标的航迹关联，其实中文中两词汇不必咬文嚼字，读者意会就好。

二、多站航迹相关算法（Multi-Station(Sensor) Track Correlation）

首先给出物理量的符号表示，以两部雷达站为例，分别对其编号为1、2，在时刻为 $l$ 时两雷达站的航迹号（目标号）集合为[1]：

$U_{1}=\{1,2,\cdots,n_{1}\},U_{2}=\{1,2,\cdots,n_{2}\},$

卡尔曼滤波(Kalman Filter)过程中运动观测模型选择[2]：

$\begin{align*} \boldsymbol{X}(l)&=\boldsymbol{F}\cdot \boldsymbol{X}(l-1)+\boldsymbol{G}\cdot \boldsymbol{u}(l) \\ \boldsymbol{Z}(l)&=\boldsymbol{H}(l)\cdot \boldsymbol{X}(l)+\boldsymbol{w}(l) \end{align*}$

预测模型为：

$\begin{aligned} &\boldsymbol{\widehat{X}}(l|l-1)=\boldsymbol{F}\cdot \boldsymbol{\widehat{X}}(l-1|l-1)\\ &\boldsymbol{M}(l|l-1)=\boldsymbol{F}\cdot \boldsymbol{M}(l-1|l-1)\cdot \boldsymbol{F}^{\rm T}+\boldsymbol{GS}_{u}(l)\boldsymbol{G}^{\rm T} \end{aligned}$

其中 $\small \boldsymbol{S}_{u}(l)$ 是 $\small \boldsymbol{u}(l)$ 的协方差矩阵。

卡尔曼滤波增益为：

$\boldsymbol{K}(l-1)= \boldsymbol{M}(l|l-1) \boldsymbol{H}^{\rm T}(l)( \boldsymbol{S}_{w}(l)+ \boldsymbol{H}(l) \boldsymbol{M}(l|l-1) \boldsymbol{H}^{\rm T}(l))^{-1}$

其中 $\small \boldsymbol{S}_{w}(l)$ 是 $\small \boldsymbol{w}(l)$ 的协方差矩阵。

状态估计值和估计均方误差为：

$\begin{aligned} &\boldsymbol{\widehat{X}}(l|l)=\boldsymbol{\widehat{X}}(l|l-1)+\boldsymbol{K}(l)(\boldsymbol{Z}(l)-\boldsymbol{H}(l)\boldsymbol{\widehat{X}}(l|l-1))\\ &\boldsymbol{M}(l|l)=(\boldsymbol{I}-\boldsymbol{K}(l)\boldsymbol{H}(l))\boldsymbol{M}(l|l-1) \end{aligned}$

对上述变量附加上下角标可表示相应雷达和相应航迹号下的物理量，例如 $\small \boldsymbol{X}^{1}_{i}(l)$ 表示 $\small l$ 时刻雷达站1对应航迹号为 $\small i\in U_{1}$ 的目标状态真实值。

设 $\small H_{0}$ 和 $\small H_{1}$ 表示如下事件：

$\small H_{0}:$ $\small \boldsymbol{\widehat{X}}_{i}^{1}(l|l)$ 和 $\small \boldsymbol{\widehat{X}}_{j}^{2}(l|l)$ 是同一目标的状态估计；

$\small H_{1}:$ $\small \boldsymbol{\widehat{X}}_{i}^{1}(l|l)$ 和 $\small \boldsymbol{\widehat{X}}_{j}^{2}(l|l)$ 不是同一目标的状态估计；

至此可以看到，航迹相关就是解决以上的二元假设问题。

2.1 加权与修正航迹相关算法

直观上，判断两个估计量是否源于同一目标的准则是看两者的相关性或者说是相近性，定量形式则表现为“距离”。考虑到状态估计向量中各物理量的尺度不同，利用马氏距离来衡量估计量间的相近性更为合适，若假设两雷达站对同一目标的状态估计是统计独立的，则该种情况下检验统计量为[1]：

$\begin{aligned} &\alpha_{ij}=(\boldsymbol{\widehat{X}}_{i}^{1}(l|l)-\boldsymbol{\widehat{X}}_{j}^{2}(l|l))'\boldsymbol{C}_{ij}(l|l)^{-1}(\boldsymbol{\widehat{X}}_{i}^{1}(l|l)-\boldsymbol{\widehat{X}}_{j}^{2}(l|l))\\ &\boldsymbol{C}_{ij}(l|l)=\boldsymbol{M}_{i}^{1}(l|l)+\boldsymbol{M}_{j}^{2}(l|l) \end{aligned}$

该表达式也可通过Neyman-Pearson准则进行推导得到，具体的，令 $\small t_{ij}(l)$ 表示：

$\boldsymbol{t}_{ij}(l)=\boldsymbol{\widehat{X}}_{i}^{1}(l|l)-\boldsymbol{\widehat{X}}_{j}^{2}(l|l)$

则有以下似然函数：

$\begin{aligned} &p(\boldsymbol{t}_{ij}(l)|H_{0})=\frac{1}{(2\pi)^{m/2}|\boldsymbol{C}_{ij}(l|l)|^{1/2}} {\rm e}^{-\frac{1}{2}\boldsymbol{t}_{ij}(l)'\boldsymbol{C}_{ij}(l|l)^{-1}\boldsymbol{t}_{ij}(l)}\\ &p(\boldsymbol{t}_{ij}(l)|H_{1})=V^{-1} \end{aligned}$

其中 $m$ 表示状态向量维数， $V$ 表示整个状态空间大小。对数似然比为：

$\Lambda = {\rm ln}\frac{p(\boldsymbol{t}_{ij}(l)|H_{1})}{p(\boldsymbol{t}_{ij}(l)|H_{0})}$

对其进行化简可以得到上面检验统计量 $\alpha_{ij}$ 表达式的形式，且其服从自由度为 $m$ 的 $\chi^{2}$ 分布，若令虚警率控制在 $P_{\rm fa}$ ，则得到判决门限为：

$\lambda_{\alpha}=\underset{\lambda}{\rm arg}\{{\rm P}\{\alpha_{ij}>\lambda|H_{0}\}=P_{\rm fa}\}$

令 $\alpha_{ij}$ 与门限值 $\lambda_{\alpha}$ 进行比较，可得到判决模型如下：

$\alpha_{ij} \begin{matrix} H_{1}\\ >\\ <\\ H_{0} \end{matrix}\lambda_{\alpha}$

从以上的相关算法中可以看到， $\alpha_{ij}$ 是内积的形式，其利用协方差系数对估计量差值进行加权，因此这种关联算法也叫做加权航迹相关算法。

考虑到来自两个雷达站的估计误差并不总是完全独立，来自同一目标的估计量可能会存在相关的过程处理噪声，因此当两个雷达站的估计误差并不总是完全独立时，检验统计量修正为：

$\begin{aligned} &\beta_{ij}=(\boldsymbol{\widehat{X}}_{i}^{1}(l|l)-\boldsymbol{\widehat{X}}_{j}^{2}(l|l))'\boldsymbol{B}_{ij}(l|l)^{-1}(\boldsymbol{\widehat{X}}_{i}^{1}(l|l)-\boldsymbol{\widehat{X}}_{j}^{2}(l|l))\\ &\boldsymbol{B}_{ij}(l|l)=\boldsymbol{M}_{i}^{1}(l|l)+\boldsymbol{M}_{j}^{2}(l|l)-\boldsymbol{M}_{ij}^{12}(l|l)-\boldsymbol{M}_{ij}^{12}(l|l)' \\ &\boldsymbol{M}_{ij}^{12}(l|l)=[\boldsymbol{I}-\boldsymbol{K}_{i}^{1}\boldsymbol{H}^{1}(l)][\boldsymbol{F}\cdot \boldsymbol{M}_{ij}^{12}(l-1|l-1)\cdot \boldsymbol{F}^{\rm T}+\boldsymbol{GS}_{u}\boldsymbol{G}^{\rm T}] [\boldsymbol{I}-\boldsymbol{K}_{i}^{1}\boldsymbol{H}^{1}(l)]' \end{aligned}$

判决模型为：

$\beta_{ij} \begin{matrix} H_{1}\\ >\\ <\\ H_{0} \end{matrix}\lambda_{\beta}$

这就是修正过的航迹加权方法。

需要提出的是，上面过程中将 $\small p(\boldsymbol{t}_{ij}(l)|H_{1})$ 建模为了均匀分布，这是一种理想且简单的建模方法，而文献[3]则对该概率函数给出了一套建模方法，并给出了该模型下的检验统计量表达形式以及相应的简化形式。此外，文献[3]还给出了多站相关算法的相关错误类型及建模计算，并以此给出了门限最优化方法，有兴趣的读者可以参考学习。

此外文献[4]给出了 $\small \boldsymbol{M}_{ij}^{12}(l|l)$ 的建模计算方式，可供大家参考。

2.2 序贯航迹相关算法

加权法和修正法由于仅通过单次估计进行相关，因此在目标环境较密集、交叉和分叉航迹较多的场合下会出现大量错、漏关联航迹情况。为此，考虑将航迹的历史信息融入到航迹相关中来，利用历史信息增益增强相关可靠性，这就是序贯相关算法。

同2.1节中推导过程一致，依据Neyman-Pearson准则可以得到序贯关联算法下的检验统计量为[1]：

$\begin{aligned} &\lambda_{ij}(k)=\sum_{l=1}^{k}\boldsymbol{t}_{ij}(l)'\boldsymbol{C}_{ij}(l|l)^{-1}\boldsymbol{t}_{ij}(l)=\lambda_{ij}(k-1)+\boldsymbol{t}_{ij}(k)'\boldsymbol{C}_{ij}(k|k)^{-1}\boldsymbol{t}_{ij}(k) \end{aligned}$

规定 $\small \lambda_{ij}(0)=0$ 。该检验统计量服从自由度 $km$ 的 $\chi^{2}$ 分布，判决模型为：

$\lambda_{ij}(k) \begin{matrix} H_{1}\\ >\\ <\\ H_{0} \end{matrix}\delta(k)$

注意到上面的协方差矩阵是以估计误差独立为假设前提的，所以这也叫独立序贯法。若把 $\small \boldsymbol{C}_{ij}(l|l)$ 换为 $\small \boldsymbol{B}_{ij}(l|l)$ ，则考虑到了误差相关的情况，这种关联算法叫做相关序贯法。

需要注意的是，随着 $k$ 值的增加，根据协方差矩阵的非负定性， $\small \lambda_{ij}(k)$ 的值也在增大，为保证固定的虚警率 $P_{\rm fa}$ ，门限 $\small \delta(k)$ 也需要增大。

考虑到与新数据较近时刻的数据对实时的判决更有参考价值，因此可考虑有限记忆的航迹关联准则和衰减记忆的航迹关联准则，其序贯递推形式如下：

有限记忆的航迹关联准则：

$\small \begin{aligned} &\theta_{ij}(k)=\sum_{l=k+1-k_{0}}^{k}\boldsymbol{t}_{ij}(l)'\boldsymbol{C}_{ij}(l|l)^{-1}\boldsymbol{t}_{ij}(l)=\theta_{ij}(k-1)+\boldsymbol{t}_{ij}(k)'\boldsymbol{C}_{ij}(k|k)^{-1}\boldsymbol{t}_{ij}(k) -\boldsymbol{t}_{ij}(k-k_{0})'\boldsymbol{C}_{ij}(k-k_{0}|-k_{0})^{-1}\boldsymbol{t}_{ij}(k-k_{0}) \end{aligned}$

衰减记忆的航迹关联准则：

$\small \varphi_{ij}(k)=\sum_{l=1}^{k}\gamma^{l-1}\boldsymbol{t}_{ij}(l)'\boldsymbol{C}_{ij}(l|l)^{-1}\boldsymbol{t}_{ij}(l)=\gamma\varphi_{ij}(k-1)+\boldsymbol{t}_{ij}(k)'\boldsymbol{C}_{ij}(k|k)^{-1}\boldsymbol{t}_{ij}(k)$

其中 $\small \gamma$ 为遗忘系数或折扣系数。上两式中均可将 $\small \boldsymbol{C}_{ij}(l|l)$ 换为 $\small \boldsymbol{B}_{ij}(l|l)$ 。

2.3 统计双门限航迹相关算法

另外一种解决加权法和修正法在密集目标场景下发生错、漏关联问题的算法叫做统计双门限方法。所谓“双门限”，第一门限是根据加权法或修正法依次对数据进行初步门限比较，若判为 $\small H_{0}$ 则计数器加1，若 $\small R$ 次判决中至少有 $\small L$ 次的判决结果为 $\small H_{0}$ ，则可判定两条航迹源于同一目标[1]。

具体的，对于时刻 $\small l=1,2,\cdots,R$ ，依次进行加权法或修正法的判决，若

$\small \alpha_{ij}(l)\leq\delta_{\alpha} \ {\rm or}\ \beta_{ij}(l)\leq\delta_{\beta}$

则 $\small m_{ij}(l)=m_{ij}(l-1)+1(m_{ij}(0)=0)$ ，当 $\small m_{ij}(l)\geq L$ 时，则可判定雷达站1的航迹 $\small i$ 与雷达站2的航迹 $\small j$ 为同一目标。由于判定结果依据了所有历史信息，因此双门限方法的相关性能要优于加权法和修正法。

2.4 最近邻域航迹相关算法（Nearest Neighbor，NN）

独立于加权法和修正法的另一基本关联方法为最近邻域法。2.1节中已经定义，雷达站1的航迹 $\small i$ 与雷达站2的航迹 $\small j$ 在 $l$ 时刻的状态估计差为[1]：

$\boldsymbol{t}_{ij}(l)=\boldsymbol{\widehat{X}}_{i}^{1}(l|l)-\boldsymbol{\widehat{X}}_{j}^{2}(l|l)=[u_{ij}(1,l),u_{ij}(2,l),\cdots,u_{ij}(m,l)]'$

设阈值矢量为 $\boldsymbol{e}=(e_{1},e_{2},\cdots,e_{m})$ ，则当以下式子成立时：

$\small L_{ij}(l)=(|u_{ij}(l,1)<e_{1}|)\cap(|u_{ij}(l,2)<e_{2}|)\cap\cdots\cap(|u_{ij}(l,m)<e_{m}|)=1$

可判定 $\small H_{0}$ 假设成立，否则为 $\small H_{1}$ 。

2.5 K近邻域（K-Nearest Neighbor，K-NN）与修正的K近邻域航迹相关算法（Modified K-Nearest Neighbor, MK-NN）

类似于加权法和修正法，最近邻方法仅基于单次估计值进行关联，因此也会在密集目标环境下表现出较差的相关性能。类似于统计双门限方法对加权法和修正法的改善，一种基于历史信息和多次测量数据的最近邻算法改善方法就是K近邻方法[1]。

设置总关联检测次数为 $\small N_{0}$ ，门限值 $\small K$ 为正整数，如果在 $\small N_{0}$ 次判决中至少有 $\small K$ 次满足：

$L_{ij}(l)=1$

则判定为 $\small H_{0}$ ，否则为 $\small H_{1}$ 成立。

其中门限值 $\small K=[\mu\cdot N_{0}]$ ， $\small [\cdot]$ 表示取整， $\small \mu$ 的取值范围一般为 $\small (0.5,0.75]$ 。总关联次数 $\small N_{0}$ 选取过大会加重存储量和计算负担，选择过小会影响关联性能，因此一般取值范围为 $\small [6,12]$ 。 $\small N_{0}$ 的取值也有实际场景有关，目标较密集取值增大，目标速度越高取值减小，采样间隔增大取值减小。

上述关联条件是K近邻的核心算法，形式上比较容易理解，但是在工程实践中为了进一步提高关联的准确性和可操作性，K近邻算法具体实施流程包括了建立期、相关期、巩固期、检查期和保持期五个阶段，文献[5]对这五个阶段进行了详细介绍，但笔者感觉该论文一方面印刷排版质量较差、数学描述较抽象、其具体过程也比较复杂，有兴趣和能力的读者可进行参考学习，这里就不加赘述了。

好在后来提出的修正K近邻航迹[1]相关算法在处理过程上优化了K近邻的算法操作，简化了算法结构，这在一定程度上提高了K近邻的算法速度和工程可实现性，同时提高了相关性能，也让笔者免受文献[5]的理解之苦。

在叙述MK-NN算法之前，首先给出两个描述航迹质量的两个参数：

航迹相关质量： $\small N_{0}$ 次判决中判决为 $\small H_{0}$ 的次数 $\small m_{ij}(l)$ ；

航迹脱离质量： $\small N_{0}$ 次判决中判决为 $\small H_{1}$ 的次数 $\small D_{ij}(l)$ ；

具体的，如果 $\small L_{ij}(l)=1$ ，则:

$m_{ij}(l)=m_{ij}(l-1)+1,m_{ij}(0)=0$

否则：

$D_{ij}(l)=D_{ij}(l-1)+1,D_{ij}(0)=0$

MK-NN算法将整个算法流程分为相关期、检查期和保持期，以下将对各阶段作以介绍。

（1）相关期（ $\small l=1,2,\cdots,N_{0}$ ）

依次对各时刻的状态估计差值进行基于NN算法的判决，其中各维误差阈值可由下面自适应公式确定：

$e_{q}(l)=G_{c}[M_{qq}^{1}(i,l)+M_{qq}^{2}(i,l)]^{1/2}$

其中 $\small M_{qq}^{1}(i,l),M_{qq}^{2}(i,l)$ 分别为在 $\small l$ 时刻雷达站1的航迹 $\small i$ 和雷达站2的航迹 $\small j$ 的状态估计协方差矩阵的第 $\small q$ 个对角线元素。 $\small G_{c}$ 为阈值系数，正常情况下取3，当目标为高机动目标时取5，这是经验取值。当 $\small l$ 时刻雷达站1的航迹 $\small i$ 无法和雷达站2的任何航迹满足NN相关时，可令 $\small G_{c}=5$ 适当扩大门限重新进行NN相关，以此来防止漏相关。

当 $\small l$ 时刻满足 $\small D_{ij}(l)> N_{0}-K$ 时，说明雷达站1的航迹 $\small i$ 和雷达站2的航迹 $\small j$ 已经无关成为相关对，下一时刻无须再对这两条航迹进行相关。当 $\small N_{0}$ 时刻存在某雷达站的某条航迹与另一雷达站的多条航迹满足相关，也即满足 $\small m_{ij}(N_{0})\geq K$ 时，则需要进行多义性处理，以保证任意时刻每个雷达站的每条航迹只能与其它雷达的一条航迹进行相关，多义性处理会在后面进行归纳介绍，这里先按下不讲。

当然，也会存在 $\small N_{0}$ 时刻雷达站1的航迹 $\small i$ 无法与雷达站2的任何航迹形成相关对的情况，但若满足：

$\begin{aligned} &j^{*}=\underset{j'\in U_{2}}{\rm arg\ max}\ m_{ij'}(N_{0})\\ &m_{ij^{*}}\geq K \end{aligned}$

且 $\small j^{*}$ 已经与 $\small U_{1}$ 中的某条航迹形成相关对时，可将 $\small i$ 和 $\small j^{*}$ 形成冗余相关输出，否则将 $\small i$ 作为孤立航迹输出。同样的过程可应用于雷达站2中未形成相关对的航迹。

（2）检查期（ $\small l=N_{0}+1,N_{0}+2,N_{0}+3(,N_{0}+4,N_{0}+5)$ ）

考虑到检查期存在错误相关对的可能，设立检查期对相关对进行进一步检查。具体的，首先对 $\small l=N_{0}+1,N_{0}+2,N_{0}+3$ 进行相关判决，如果

$\small \omega_{ij}(l)=\beta(\boldsymbol{\widehat{X}}_{i}^{1}(l|l)-\boldsymbol{\widehat{X}}_{j}^{2}(l|l))'\boldsymbol{C}_{ij}(l|l)^{-1}(\boldsymbol{\widehat{X}}_{i}^{1}(l|l)-\boldsymbol{\widehat{X}}_{j}^{2}(l|l))\leq\delta$

则 $\small T_{ij}(l)=T_{ij}(l-1)+1(T_{ij}(N_{0})=0)$ ，否则 $\small T_{ij}(l)=T_{ij}(l-1)-1$ 。上式中 $\small \beta$ 是用以弥补过程噪声估计不足而设定的修正系数， $\small \delta$ 是判决门限。当 $\small l=N_{0}+3$ 时，若 $\small T_{ij}(N_{0}+3)=3$ ，则 $\small i$ 和 $\small j$ 形成固定相关对，进入保持期；若 $\small T_{ij}(N_{0}+3)\leq-1$ ，则撤销 $\small i$ 和 $\small j$ 所对应的系统航迹，重新进入相关期；若 $\small T_{ij}(N_{0}+3)=1$ ，则需要再进行两次检验，然后根据 $\small T_{ij}(N_{0}+5)$ 的取值作最终的判决。

（3）保持期（ $\small l>N_{0}+3({\rm or}\ N_{0}+5)$ ）

通过检查期的相关对一旦进入保持期，就不需要在进行假设检验和正确性检查，只需接收相应航迹新一时刻的点迹并进行航迹融合处理即可。

2.6 多义性处理

上述的关联过程中共同面对的一个问题是可能存在某雷达站的某条航迹与其它雷达站的多条航迹可以相关上的情况，这种情况下就需要进行多义性处理。对于序贯、统计双门限、K-NN以及MK-NN航迹相关算法而言，比较常用的多义性处理方式为选择航迹相关质量最高的航迹对，即[1]：

$j^{*}=\underset{j\in \boldsymbol{J}}{\rm arg\ max} \ m_{ij}(N_{0})$

其中 $\small \boldsymbol{J}$ 是使 $\small m_{ij}(N_{0})\geq K$ 成立的航迹 $\small j$ 集合。若满足上式的 $\small j^{*}$ 不只一个，则需要进一步多义性处理，一种第二步多义性处理方式是选择航迹位置差矢量序列的平均范数最小的相关对，即：

$j^{'*}=\underset{j^{*}\in\boldsymbol{J}^{*}}{\rm arg\ min} \ \frac{1}{N_{0}}(\sum_{l=1}^{N_{0}}\begin{Vmatrix} \bar{X}_{ij^{*}}(l) \end{Vmatrix})$

其中 $\small \boldsymbol{J^{*}}$ 是 $\small j^{*}$ 的集合， $\small \bar{X}_{ij^{*}}(l)$ 表示航迹 $\small i$ 和 $\small j^{*}$ 在 $\small l$ 时刻的位置差矢量。

另外一种第二步多义性处理方式是选择平均检验统计量最小的航迹对：

$j^{'*}=\underset{j^{*}\in\boldsymbol{J}^{*}}{\rm arg\ min} \ \frac{1}{N_{0}}\sum_{l=1}^{N_{0}}\alpha_{ij^{*}}(l) ({\rm or}\ \beta_{ij^{*}}(l))$

其实这种方法也是一种最大似然的方法，这样选择的航迹对在 $\small H_{0}$ 假设条件下的似然概率最高。

2.7 多雷达站航迹相关算法

前面介绍的算法是在两雷达站情况下进行讨论的，而对于含有大于等于3部雷达站的组网下航迹的相关方法需要进一步讨论[1]。

一种比较直观的方法是根据相关的可传递性，对 $\small M$ 个雷达站共同监视区域内的航迹进行顺序两两相关。需要注意的是，可能会存在部分区域只能被某些雷达站共同监测，这时只需对这些雷达站进行顺序两两相关即可。

此外还有一种相关方法为多维分配方法，其通过建立以损失函数的和最小值为目标函数的优化模型，求解最优解对应的相关方法。例如2.2节中已经给出了序贯航迹相关算法的检验统计量：

现构造一个全局统计量：

$a_{i_{1}i_{2}\cdots i_{M}}(l)=\sum_{s=2}^{M}\lambda_{i_{s-1}i_{s}}(l)$

其中 $\small i_{1}i_{2}\cdots i_{M}$ 分别表示雷达站 $\small 1\sim M$ 的某航迹。定义一个二进制变量表示一种关联事件：

$\eta_{i_{1}i_{2}\cdots i_{M}}(l)=\left\{\begin{matrix} 1 & H_{0}\ holds\\ 0 & H_{1}\ holds \end{matrix}\right.$

则以某雷达站的某条航迹只能与其它雷达站的一条航迹进行相关为约束条件，以全局统计量最小值为目标函数建立如下优化模型：

$\begin{aligned} &\underset{\eta_{i_{1}i_{2}\cdots i_{M}}}{\rm min}\sum_{i_{1}=1}^{n_{1}}\sum_{i_{2}=1}^{n_{2}}\cdots\sum_{i_{M}=1}^{n_{M}}\eta_{i_{1}i_{2}\cdots i_{M}}a_{i_{1}i_{2}\cdots i_{M}}(l)\\ &\left\{\begin{matrix} \sum_{i_{2}=1}^{n_{2}}\sum_{i_{3}=1}^{n_{3}}\cdots\sum_{i_{M}=1}^{n_{M}}\eta_{i_{2}i_{3}\cdots i_{M}}=1 & \forall i_{1}=1,2,\cdots,n_{1}\\ \sum_{i_{1}=1}^{n_{1}}\sum_{i_{3}=1}^{n_{3}}\cdots\sum_{i_{M}=1}^{n_{M}}\eta_{i_{1}i_{3}\cdots i_{M}}=1 & \forall i_{2}=1,2,\cdots,n_{2} \\ \sum_{i_{1}=1}^{n_{1}}\sum_{i_{2}=1}^{n_{2}}\cdots\sum_{i_{M-1}=1}^{n_{M-1}}\eta_{i_{1}i_{2}\cdots i_{M-1}}=1 & \forall i_{M}=1,2,\cdots,n_{M} \end{matrix}\right. \end{aligned}$

可以看到这是一个整数规划问题，这种方法又被称为经典分配法。该种方法在约束条件中规定了航迹相关的唯一性，因此也同时考虑进了多义性处理的问题。

2.8 一种K-means聚类的航迹相关算法

文献[6]提出了一种基于K-means聚类的航迹相关算法，不同与上述局部雷达站的相互相关，该方法完成的是局部雷达站的航迹与系统航迹的相关。

首先给出局部雷达站航迹号集合和系统航迹集合为：

$\boldsymbol{x}_{p}=\{x_{p1},x_{p2},\cdots,x_{pn_{p}}\};\boldsymbol{x}_{s}=\{x_{s1},x_{s2},\cdots,x_{sn_{s}}\}$

其中 $n_{p}$ 和 $n_{s}$ 分别表示局部雷达站航迹和系统航迹的航迹号数量。

定义每个航迹号对应一个状态向量 $\small \boldsymbol{x}_{\alpha}$ 和一个位置向量 $\small \boldsymbol{x}_{\beta}$ ，该文献中定义了一种新的衡量两条航迹相关性的距离测度：

$d_{ij}=\begin{Vmatrix} \boldsymbol{x}_{\alpha i}-\boldsymbol{x}_{\alpha j} \end{Vmatrix}_{1}+\begin{Vmatrix} \boldsymbol{x}_{\beta i}-\boldsymbol{x}_{\beta j}\end{Vmatrix}_{2},i\in\boldsymbol{x}_{p},j\in\boldsymbol{x}_{s},$

其中状态向量 $\small \boldsymbol{x}_{\alpha}$ 各维物理量表示目标状态，位置向量 $\small \boldsymbol{x}_{\beta}$ 各维物理量表示目标位置坐标。

根据系统航迹个数将航迹分为 $n_{s}$ 类，每个局部雷达站的航迹与各系统航迹进行距离测度计算，选择距离测度最小的进行归类，即：

$j^{*}=\underset{j\in \boldsymbol{x}_{s}}{\rm arg\ min} \ d_{ij}$

为了排除异常点和孤立点，还需进行一步门限判决，若 $\small d_{ij^{*}}\leq\delta_{d}$ ，则接受分类，否则不接受。需要注意的是，上面的归类相关方法也会存在某一时刻同一雷达站的多条航迹被分到同一类系统航迹的情况，因此还需要进行多义性处理。文献[6]给出的方式比较直接，即将距离测度较小的航迹归到其距离测度次大的系统航迹类中，重复进行此操作直到无多义性情况存在为止。

多义性处理之后，利用刚相关的局部航迹数据对其归类的系统航迹进行加权修正，之后计算修正过的系统航迹与其对应的局部航迹的中心离散程度指标，比如量化为均方差，若该指标小于某一门限值则完成相关归类操作，否则基于更新过的系统航迹再进行上述的相关操作。

三、联合概率数据关联（Joint Probabilistic Data Association, JPDA）

联合概率数据关联（Joint Probabilistic Data Association, JPDA）是一种应用于多目标跟踪的航迹关联算法。不同与第二节提到的多站之间的航迹相关，JPDA算法不对每个传输到融合中心的状态观测点进行是否属于某一目标航迹的假设检验，而是对落入目标确认波门（Validation Gate）的每个状态观测点进行加权求和，加权系数为观测点和目标可以关联的后验概率，加权求和结果用于目标的状态更新。

本部分内容主要参考的是文献[7]，物理符号也大都与该文献中一致。

3.1 符号描述

假设在 $\small k$ 时刻落入雷达站观测区域的有 $\small m$ 个观测点，这些观测点对应的状态向量集合为：

$\boldsymbol{Z}(k)=\{\boldsymbol{y_{j}}\}_{j=1}^{m}$

直到 $\small k$ 时刻所有的观测点对应的状态向量集合为：

$\boldsymbol{Z}^{k}=\{\boldsymbol{Z}(k),\boldsymbol{Z}^{k-1}\}$

假设观测区域有 $\small T$ 个现存目标，目标 $\small t$ 的预测状态向量为 $\small \hat{\boldsymbol{y}}^{t}$ ，则观测点 $\small j$ 相对于目标 $\small t$ 的新息为：

$\tilde{\boldsymbol{y}}^{t}_{j}=\boldsymbol{y}_{j}-\hat{\boldsymbol{y}}^{t}$

对 $\small m$ 个观测点相对于目标 $\small t$ 的新息加权求和得到目标 $\small t$ 的平均新息估计：

$\tilde{\boldsymbol{y}}^{t}=\sum_{j=1}^{m}\beta_{j}^{t}\tilde{\boldsymbol{y}}^{t}_{j}$

其中 $\small \beta_{j}^{t}$ 为加权系数， $\small \beta_{0}^{t}$ 表示没有任何观测点和目标 $\small t$ 的航迹相关联。得到平均新息估计后可进行卡尔曼滤波。以下几部分对加权系数 $\small \beta_{j}^{t}$ 进行建模计算。

3.2 确认逻辑和确认矩阵

定义事件 $\small \chi_{jt_{j}}$ 表示观测点 $\small j$ 来自目标 $\small t_{j}$ 且 $\small 0\leq t_{j}\leq T$ ， $\small t_{j}=0$ 表示观测点 $\small j$ 无法与任何已存目标进行关联，则整体关联事件可表示为：

$\small \chi=\bigcap_{j=1}^{m}\chi_{jt_{j}}$

现定义两个二元变量：

$\begin{aligned} &\tau_{j}(\chi)\triangleq\left\{\begin{matrix} 1 & {\rm if}\ t_{j}>0\\ 0 & {\rm if}\ t_{j}=0 \end{matrix}\right.\\ &\delta_{t}(\chi)\triangleq\left\{\begin{matrix} 1 & {\rm if}\ t_{j}=t\ {\rm for\ some\ j}\\ 0 & {\rm if}\ t_{j}\neq t\ {\rm for\ all\ j} \end{matrix}\right. \end{aligned}$

可见 $\small \tau_{j}(\chi)$ 表示观测点 $\small j$ 是否和某个现存目标关联， $\small \delta_{t}(\chi)$ 表示目标 $t$ 是否与某个观测点关联。

再定义一个确认矩阵：

$\boldsymbol{\Omega}=[\omega_{jt}], j=1,2,\cdots,m;t=0,1,\cdots,T$

其元素 $\small \omega_{jt}$ 为二元数值，表示观测点 $\small j$ 是否在目标 $t$ 的确认波门中，即表示观测点 $\small j$ 可能源于目标 $t$ 。确认波门可由下式描述[8]：

$\begin{aligned} &\boldsymbol{Y}^{t}=\{\boldsymbol{y}|(\boldsymbol{y}-\hat{\boldsymbol{y}}^{t})'\boldsymbol{S}_{t}^{-1}(\boldsymbol{y}-\hat{\boldsymbol{y}}^{t})\leq d\}\\ &\boldsymbol{S}_{t}=\boldsymbol{H}_{t}\boldsymbol{M}_{t}(k|k-1)\boldsymbol{H}_{t}'+\boldsymbol{S}_{w,t} \end{aligned}$

其中 $\small \boldsymbol{S}_{t}$ 为目标 $\small t$ 的新息协方差矩阵， $\small \boldsymbol{H}_{t},\boldsymbol{M}_{t}(k|k-1),\boldsymbol{S}_{w,t}$ 为目标 $\small t$ 对应的卡尔曼滤波参数。 $\small t=0$ 表示观测点 $\small j$ 可能来自杂波或者虚警，因此确认矩阵 $\boldsymbol{\Omega}$ 的第一列 $\small (t=0)$ 都为1。图1是一个确认波门和对应确认矩阵 $\boldsymbol{\Omega}$ 的例子，帮助大家理解。

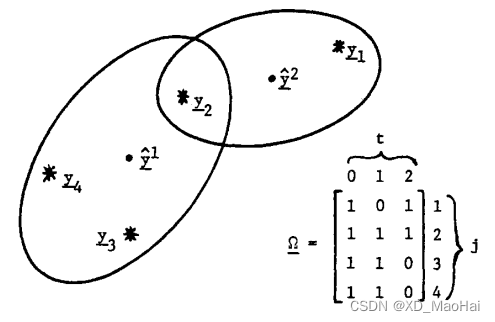
由上述定义可知，每个关联事件 $\small \chi$ 均可用一个矩阵表述：

$\begin{aligned} &\hat{\boldsymbol{\Omega}}(\chi)=[\hat{\omega}_{jt}(\chi)]\\ &\hat{\omega}_{jt}(\chi)=\left\{\begin{matrix} 1 & {\rm if}\ \chi_{jt}\ {\rm occurs}\\ 0 & {\rm otherwise} \end{matrix}\right. \end{aligned}$

为保证关联事件 $\small \chi$ 为合理事件（Feasible Event），需满足以下两个条件：

$\small \hat{\boldsymbol{\Omega}}(\chi)$ 每行之和为1，以保证每个观测点只可能源于一个目标；
$\small \hat{\boldsymbol{\Omega}}(\chi)$ 每列之和不大于1 $\small (t=1,2,\cdots,T)$ ，以保证每个目标在同一时刻只可能有一个观测点，但对第一列 $\small (t=0)$ 没有此限制条件；

由上述内容可知，一个时刻的确认矩阵可能对应多个合理事件，将这些合理事件归入同一集合 $\small \boldsymbol{\chi}$ ，因此也可扫描出多个不同的矩阵 $\small \hat{\boldsymbol{\Omega}}$ 。：

$\begin{aligned} &\tau_{j}(\chi)=\sum_{t=1}^{T}\hat{\omega}_{it}(\chi),\forall\ \chi\in\boldsymbol{\chi}\\ &\delta_{t}(\chi)=\sum_{j=1}^{m}\hat{\omega}_{it}(\chi),\forall\ \chi\in\boldsymbol{\chi} \end{aligned}$

3.3 加权系数和联合概率

3.1节已经给出了加权系数 $\small \beta_{j}^{t}$ 的定义，现将其量化为：

$\beta_{j}^{t}=\sum_{\chi\in\boldsymbol{\chi}}{\rm P}\{\chi|\boldsymbol{Z}^{k}\}\hat{\omega}_{it}(\chi)$

上式通过联合后验概率对权系数进行建模是一种符合人们直观认识的方式，也是比较符合实际情况的方式，这是因为相较于概率数据关联（Probabilistic Data Association, PDA）[8]独立的去计算 $\small \beta_{j}^{t}$ ，也即假设未与目标 $\small t$ 相关联的观测点均为独立杂波点，JPDA考虑了不同目标对应的观测点关联情况的相关性，因此用联合概率 $\small {\rm P}\{\chi|\boldsymbol{Z}^{k}\}$ 而非 $\small {\rm P}\{\chi_{jt}|\boldsymbol{Z}^{k}\}$ 来对 $\small \beta_{j}^{t}$ 建模。

以下就要处理 $\small {\rm P}\{\chi|\boldsymbol{Z}^{k}\}$ 的建模计算问题了。首先根据贝叶斯准则（Bayes' Rule）有:

${\rm P}\{\chi|\boldsymbol{Z}^{k}\}=\frac{1}{c}\small {\rm P}\{\boldsymbol{Z}(k)|\chi,\boldsymbol{Z}^{k-1}\}{\rm P}\{\chi|\boldsymbol{Z}^{k-1}\}$

其中 $\small c$ 为归一化因子。由于 $\chi$ 为合理事件，其子事件相互独立，因此有：

${\rm P}\{\boldsymbol{Z}(k)|\chi,\boldsymbol{Z}^{k-1}\}=\prod_{j=1}^{m} {\rm P}\{\boldsymbol{y}_{j}|\chi_{jt_{j}},\boldsymbol{Z}^{k-1}\}$

对上式乘积项进行建模：

${\rm P}\{\boldsymbol{y}_{j}|\chi_{jt_{j}},\boldsymbol{Z}^{k-1}\}=\left\{\begin{matrix} {\rm f}_{t_{j}}(\boldsymbol{y}_{j}) & {\rm if}\ \tau_{j}(\chi)=1\\ V^{-1} & {\rm if}\ \tau_{j}(\chi)=0 \end{matrix}\right.$

其中 $\small {\rm f}_{t_{j}}(\boldsymbol{y}_{j})$ 表示观测点 $\small j$ 来自目标 $\small t_{j}$ 的概率，通常建模为如下的矢量高斯分布：

$\begin{aligned} &{\rm f}_{t_{j}}(\boldsymbol{y}_{j})=\frac{1}{(2\pi)^{l/2}|\boldsymbol{S}_{t_{j}}|^{1/2}} {\rm e}^{-\frac{1}{2}(\tilde{\boldsymbol{y}}^{t_{j}}_{j})'\boldsymbol{S}_{t_{j}}^{-1}\tilde{\boldsymbol{y}}^{t_{j}}_{j}}\\ \end{aligned}$

其中 $l$ 为状态向量维数。 $\small V$ 表示整个状态观测空间的大小，也即假设未与目标关联的观测点状态向量服从均匀分布。

将未与目标关联的观测点数量表示为：

$\phi(\chi)=\sum_{j=1}^{m}[1-\tau_{j}(\chi)]$

则与目标关联上的观测点与目标的关联情况数可由以下排列数得到：

${\rm A}_{m-\phi(\chi)}^{m}=\frac{m!}{\phi(\chi)!}$

由于事件 $\chi$ 只是其中一种排列方式，且将杂波或虚警数量建模为服从泊松分布（Poisson Distribution），因此可得到：

${\rm P}\{\chi|\boldsymbol{Z}^{k-1}\}=\frac{1}{{\rm A}_{m-\phi(\chi)}^{m}}\prod_{t:\delta_{t}=1}{\rm P}_{\rm D}^{t}\prod_{t:\delta_{t}=0}(1-{\rm P}_{\rm D}^{t})\frac{{\rm e}^{-\lambda V}(\lambda V)^{\phi(\chi)}}{\phi(\chi)!}$

其中 $\small \lambda$ 是杂波或虚警数量密度， $\small {\rm P}_{\rm D}^{t}$ 是目标 $\small t$ 单次检测的检测概率。综合上面式子可得到：

$\begin{aligned} {\rm P}\{\chi|\boldsymbol{Z}^{k}\}&=\frac{1}{c}\small {\rm P}\{\boldsymbol{Z}(k)|\chi,\boldsymbol{Z}^{k-1}\}{\rm P}\{\chi|\boldsymbol{Z}^{k-1}\}\\ &=\frac{\lambda^{\phi}}{c}\prod_{j:\tau_{j}=1}\frac{1}{(2\pi)^{l/2}|\boldsymbol{S}_{t_{j}}|^{1/2}} {\rm e}^{-\frac{1}{2}(\tilde{\boldsymbol{y}}^{t_{j}}_{j})'\boldsymbol{S}_{t_{j}}^{-1}\tilde{\boldsymbol{y}}^{t_{j}}_{j}}\prod_{t:\delta_{t}=1}{\rm P}_{\rm D}^{t}\prod_{t:\delta_{t}=0}(1-{\rm P}_{\rm D}^{t}) \end{aligned}$

至此完成了JPDA算法的完整描述。

3.4 多站情况下的JPDA算法

文献[9]基于单站的JPDA算法提出了以下两雷达站情况下的加权方式：

$\hat{\boldsymbol{x}}^{t}=\sum_{j=1}^{m_{1}}\sum_{l=1}^{m_{2}}\beta_{j,l}^{t}\hat{\boldsymbol{x}}^{t}_{j,l}$

其中 $\small m_{1},m_{2}$ 是 $\small k$ 时刻两雷达站的观测点数量。 $\small \hat{\boldsymbol{x}}^{t}_{j,l}$ 是雷达站1的观测点 $\small j$ 和雷达站2的观测点 $\small l$ 的状态向量的融合结果，即：

$\hat{\boldsymbol{x}}^{t}_{j,l}=E[\hat{\boldsymbol{x}}^{t}|\chi_{jt}^{1},\chi_{lt}^{2},\boldsymbol{Z}^{k,1},\boldsymbol{Z}^{k,2}]$

其中 $\small \boldsymbol{Z}^{k,1},\boldsymbol{Z}^{k,2}$ 是直到 $\small k$ 时刻两雷达站的观测点集合， $\small \chi_{jt}^{1},\chi_{lt}^{2}$ 分别表示雷达站1的观测点 $\small j$ 与目标 $\small t$ 关联以及雷达站2的观测点 $\small l$ 与目标 $\small t$ 关联的事件。 $\small \beta_{j,l}^{t}$ 是加权系数，其表达式如下：

$\beta_{j,l}^{t}={\rm P}(\chi_{jt}^{1},\chi_{lt}^{2}|\boldsymbol{Z}^{k,1},\boldsymbol{Z}^{k,2})$

$\small \hat{\boldsymbol{x}}^{t}_{j,l}$ 和 $\beta_{j,l}^{t}$ 的具体计算方式可参文献[9]，这里由于篇幅就不加赘述了。

参考文献

[1] 何友. 多传感器信息融合及应用 : 第二版[M]. 电子工业出版社, 2007.

[2] 理查兹, 邢孟道, 王彤,等. 雷达信号处理基础 : Fundamentals of radar signal processing[M]. 电子工业出版社, 2008.

[3] Kosaka M , Miyamoto S , Ihara H . A track correlation algorithm for multi-sensor integration[J]. Journal of Guidance, Control, and Dynamics, 1987.

[4] Bar-Shalom, Y. On the track-to-track correlation problem[J]. IEEE Transactions on Automatic Control, 2003.

[5] 何友, 谭庆海, 蒋蓉蓉. 多传感器综合系统中的航迹相关算法[J]. 火力与指挥控制, 1989.

[6] 李素, 王运锋. 应用K-means聚类的分布式多传感器航迹关联算法[J]. 电讯技术, 2018.

[7] Fortmann, T. E. , Y. Bar-Shalom , and M. Scheffe . Multi-target tracking using joint probabilistic data association. IEEE Conference on Decision & Control Including the Symposium on Adaptive Processes, 1980.

[8] Bar-Shalom, and Y. Tracking methods in a multitarget environment. IEEE Transactions on Automatic Control ,2003.

[9] Kuo-Chu, Chang C Y , Chong Y , et al. Joint Probabilistic Data Association in Distributed Sensor Networks. American Control Conference, 1985.

XD_MaoHai

关注

8
点赞
踩
36

收藏

觉得还不错? 一键收藏
打赏
0
评论
多站航迹相关（Track Correlation）与JPDA算法

多义性处理之后，利用刚相关的局部航迹数据对其归类的系统航迹进行加权修正，之后计算修正过的系统航迹与其对应的局部航迹的中心离散程度指标，比如量化为均方差，若该指标小于某一门限值则完成相关归类操作，否则基于更新过的系统航迹再进行上述的相关操作。对于分布式系统而言，每个雷达站均有自己的数据处理系统，同时也有独立的目标跟踪和航迹形成的能力，对各雷达站的航迹信息进行融合可以提高系统的跟踪精度，但航迹融合的前提是需要解决各雷达站的哪些航迹源于同一目标的问题，这一过程叫做。个雷达站共同监视区域内的航迹进行顺序两两相关。
复制链接

扫一扫