视觉SLAM十四讲笔记第二讲三维空间刚体运动

最新推荐文章于 2024-08-22 12:29:03 发布

qq_57225906

最新推荐文章于 2024-08-22 12:29:03 发布

阅读量1.7k

点赞数 52

分类专栏： SLAM 文章标签：笔记算法计算机视觉 opencv

本文链接：https://blog.csdn.net/qq_57225906/article/details/138329135

版权

SLAM 专栏收录该内容

2 篇文章 0 订阅

订阅专栏

本讲将会学习以下内容：点与坐标系、旋转矩阵、旋转向量和欧拉角、四元数以及Eigen库的使用；首先是对必要的数学知识进行回顾：

向量运算规则

1、向量内积：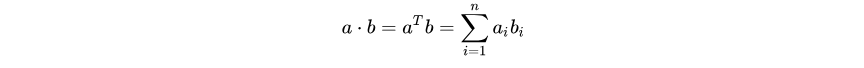

2、向量外积：

其中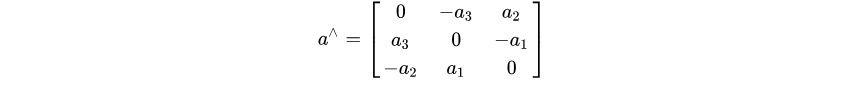

$a^{\wedge }$ 被称为列向量a的反对称矩阵（ $A^{T}= -A$ ）

补充：向量点乘和叉乘知识

点乘：

$\vec{a}=a_{1}\vec{e_{1}}+a_{2}\vec{e_{2}}+a_{3}\vec{e_{3}}$
$\vec{b}=b_{1}\vec{e_{1}}+b_{2}\vec{e_{2}}+b_{3}\vec{e_{3}}$
$\vec{e_{i}}\cdot \vec{e_{j}}=\left\{\begin{matrix} 1 &i=j \\ 0&i\neq j\end{matrix}\right.$
$\vec{a}\cdot \vec{b}= \mid\vec{a}\mid \mid\vec{b}\mid \cdot cos \theta=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$

叉乘：

$\vec{a}=a_{1}\vec{e_{1}}+a_{2}\vec{e_{2}}+a_{3}\vec{e_{3}}$
$\vec{b}=b_{1}\vec{e_{1}}+b_{2}\vec{e_{2}}+b_{3}\vec{e_{3}}$
$\vec{e_{i}}\cdot \vec{e_{j}}=\left\{\begin{matrix} 0 &i=j \\ \vec{e_{k}}&i\neq j\end{matrix}\right.$ （其中 $\vec{e_{i}}\vec{e_{j}}\vec{e_{k}}$ 方向满足右手法则）
$\vec{a}\times \vec{b}=\begin{vmatrix} \vec{e_{1}} & \vec{e_{2}} &\vec{e_{3}} \\ a_{1} & a_{2} & a_{3}\\ b_{1} & b_{2} & b_{3} \end{vmatrix}=\begin{bmatrix} a_{2}b_{3}-a_{3}b_{2}\\ a_{3}b_{1}-a_{1}b_{3} \\ a_{1}b_{2}-a_{2}b_{1} \end{bmatrix}=\begin{bmatrix} 0 & -a_{3} &a_{2} \\ a_{3}& 0 &-a_{1} \\ -a_{2}& a_{1} & 0 \end{bmatrix}b=a^{\wedge }b$

坐标系

基底：n维线性空间下的基底（e1,e2,e3...），是一组线性无关的向量；对于n维空间中的任意一个向量a，就可以由基底进行如下表示：

$a= \begin{bmatrix} e1&e2&e3 \end{bmatrix}\begin{bmatrix} a1\\a2 \\ a3 \end{bmatrix}$

其中 $\begin{bmatrix} a1 &a2 &a3 \end{bmatrix}^{T}$ 成为向量a在该基底下的坐标；坐标系一般是一组正交的线性无关的向量。

坐标系之间的欧式变换

坐标系之间的欧式变换：指刚体运动过程中，向量在各坐标系内的长度和角度不会发生变化。坐标系之间的变换通常可以拆解为两个部分：原点间的平移和三个轴的旋转；我们分开进行讨论。

旋转：记两组原点在同一位置上的基底分别为 $e$ , ${e}'$ ;同一个向量在两组基底下的坐标分别为 $a$ 和 ${a}'$ 。对于同一个向量，有下面这个等式：

$\begin{bmatrix} e1 &e2 &e3 \end{bmatrix}\begin{bmatrix} a1\\a2 \\a3 \end{bmatrix}=\begin{bmatrix} {e1}' &{e2}' & {e3}' \end{bmatrix}\begin{bmatrix} {a1}'\\{a2}' \\ {a3}' \end{bmatrix}$

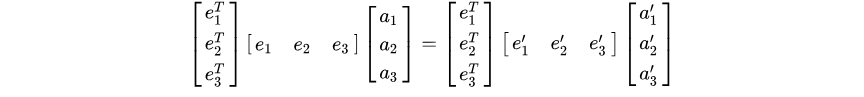两边同时左乘 $\begin{bmatrix} e1^{T} &e2^{T} &e3^{T} \end{bmatrix}^{T}$ 通过矩阵的乘法可以得到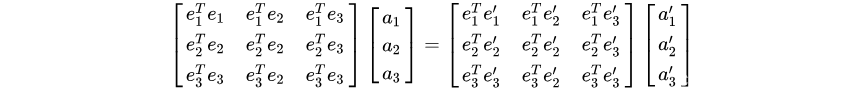：对于矩阵来说，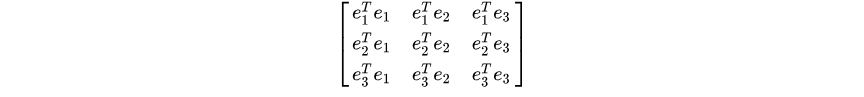

由于是两组线性无关的基底，这个矩阵是两个线性无关基底的点乘运算，一个向量在另一个向量上的投影为0，只有主对角线上的三个元素为1，其余的元素都为0；也就是说明这个矩阵是一个单位矩阵；所以原始可化简为：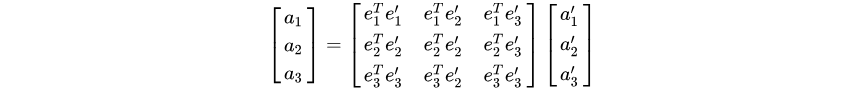

中间的矩阵，称为R，旋转矩阵。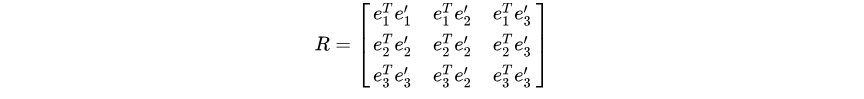

旋转矩阵

上述的R被称为旋转矩阵。作为旋转矩阵必须满足下面两条性质：一是旋转矩阵必须是正交矩阵（即其逆矩阵和转置矩阵是一致的）；二是旋转矩阵的行列式必须为1。把n维旋转矩阵记作一个集合SO(n)，称为特殊正交群。

这样就得到了坐标变换方程：满足下面关系：

由欧拉定理：刚体在三维空间里的一般运动，可分解为刚体上方某一点的平移，以及绕经过此点的旋转轴的转动。这样，通过旋转（R）加平移（t）的方式，可以得到坐标系之间的变换关系。
这里因为通过表达式去表达这种关系的方式在后续多次变换的时候会使式子表现的很复杂，所以在这里引入齐次形式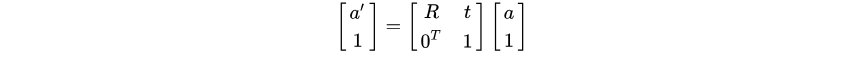：记左边这个矩阵为变换矩阵T；这样一来，可以通过左乘变换矩阵的方式来表达旋转，相比于之前用表达式表达的方式要简便许多。同时变换矩阵的逆矩阵可以用于表示一个反向的变换。这类变换矩阵的集合被称为特殊欧式群SE(3)；

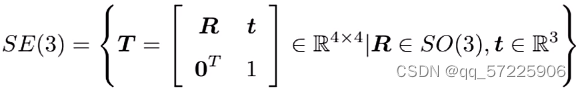
除了用旋转矩阵表示旋转外，还有其他的方式可以表示旋转，例如旋转向量、欧拉角、四元数。下面简要的介绍这些方式。

旋转向量

因为旋转矩阵SO(3)是用九个元素去表达三个自由度的信息，比较浪费，所以为了更简单的表示旋转，引入旋转向量这一表示方法。旋转向量的方向为旋转轴，长度为转过的角度。

旋转向量采用向量n表示旋转轴的方向， $\theta$ 表示绕该旋转轴旋转的角度，那么称 $\theta$ n为旋转向量。可以看出旋转向量仅用三个量就表示了旋转。（但是本质上是同一个东西的不同表达方式）旋转向量和旋转矩阵之间可以相互转换。可以用罗德里格斯公式将旋转向量转换为旋转矩阵，如下：
也可以通过下面的式子将旋转矩阵转换为旋转向量：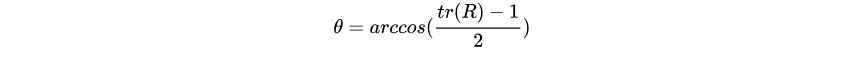
这个式子说明了n是R特征值为1的特征向量。

欧拉角

这种表示方法是将旋转分解为三个方向上的转动，例如按照Z-Y-X顺序转动，旋转轴可以是定轴也可以是动轴。常见的旋转方式由yaw-pitch-roll，不同的领域旋转的习惯有所不同；

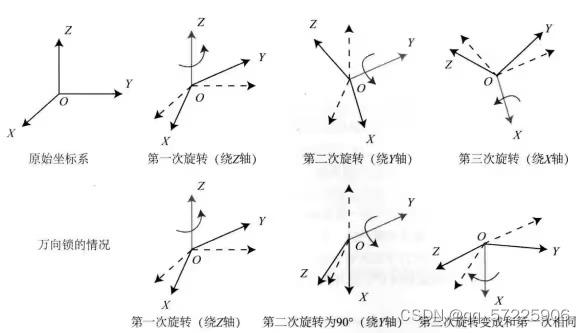
这种方法在SLAM领域不常用，原因是会遇到万向锁(Gimbal Lock)的问题,如果转轴是固定以ZYX顺序进行旋转的，如果Y旋转了±90°，可以预见，X旋转时实际上在和第一步的Z用的是同一个轴。在这种特定的情况下，旋转自由度减少了1个。而这种特殊情况在SLAM领域内却很容易遇见，所以很少用这种方法表达旋转。

四元数

我们都知道，在2维的情况下，可以用单位复数来表达旋转: $z=x+iy=\rho e^{i\theta }$ ;乘上i则旋转90°，乘上-i则转-90°。
我们联想，在三维的情况下，是否可以用复数来表示旋转呢？答案是可以的，在三维情况下，四元数可以作为复数的扩充。四元数有三个虚部和一个实部组成，它们之间满足这样的关系：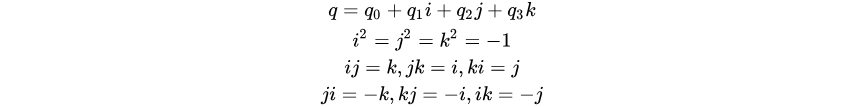

四元数的运算遵循下列法则：

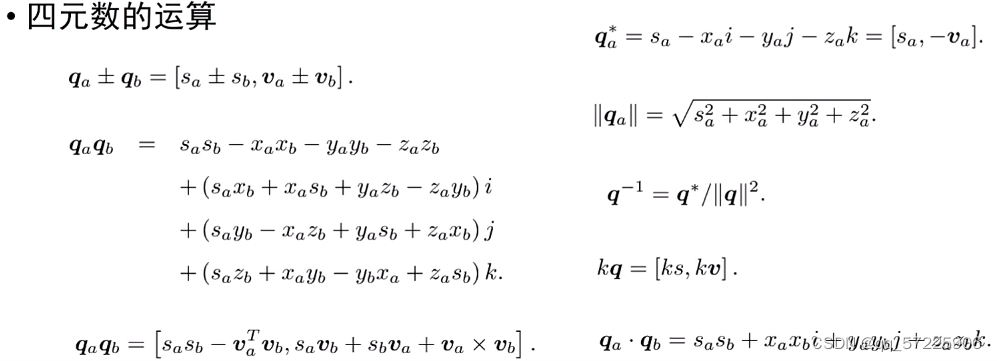
现在我们来看如何用四元数来表示旋转：设点p经过一次以q表示的旋转后，得到了 ${p}'$ ，首先将p坐标用四元数进行表示，得到旋转后的关系：
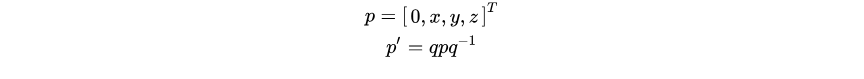
注意的是上述式子的乘法是四元数的乘法。这样就可以得到变换后的四元数坐标了。

四元数相比于旋转向量和欧拉角的优势在于：紧凑、无奇异性；不足之处在于过于抽象，很难之间通过四元数看出经过了什么样的旋转。

表达方式的相互转换

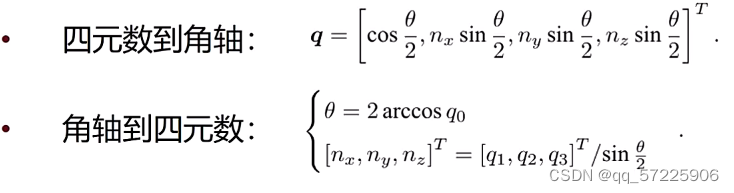
Eigen库实践

实践部分ch3中的useEigen.cpp介绍了Eigen库基本使用；代码部分如下：

#include <iostream>

using namespace std;

#include <ctime>
// Eigen 核心部分
#include <Eigen/Core>
// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Dense>

using namespace Eigen;

#define MATRIX_SIZE 50

/****************************
* 本程序演示了 Eigen 基本类型的使用
****************************/

int main(int argc, char **argv) {
  // Eigen 中所有向量和矩阵都是Eigen::Matrix，它是一个模板类。它的前三个参数为：数据类型，行，列
  // 声明一个2*3的float矩阵;Matrix是Eigen库中的一个模板类，带有模板参数
  Matrix<float, 2, 3> matrix_23; 

  // 同时，Eigen 通过 typedef 提供了许多内置类型，不过底层仍是Eigen::Matrix
  // 例如 Vector3d 实质上是 Eigen::Matrix<double, 3, 1>，即三维向量
  Vector3d v_3d;
  // 这是一样的
  Matrix<float, 3, 1> vd_3d;

  // Matrix3d 实质上是 Eigen::Matrix<double, 3, 3>
  Matrix3d matrix_33 = Matrix3d::Zero(); //初始化为零
  // 如果不确定矩阵大小，可以使用动态大小的矩阵
  Matrix<double, Dynamic, Dynamic> matrix_dynamic;
  // 更简单的
  MatrixXd matrix_x;
  // 这种类型还有很多，我们不一一列举

  // 下面是对Eigen阵的操作
  // 输入数据（初始化）
  matrix_23 << 1, 2, 3, 4, 5, 6;
  // 输出
  cout << "matrix 2x3 from 1 to 6: \n" << matrix_23 << endl;

  // 用()访问矩阵中的元素
  cout << "print matrix 2x3: " << endl;
  for (int i = 0; i < 2; i++) {
    for (int j = 0; j < 3; j++) cout << matrix_23(i, j) << "\t";
    cout << endl;
  }

  // 矩阵和向量相乘（实际上仍是矩阵和矩阵）
  v_3d << 3, 2, 1;
  vd_3d << 4, 5, 6;

  // 但是在Eigen里你不能混合两种不同类型的矩阵，像这样是错的
  // Matrix<double, 2, 1> result_wrong_type = matrix_23 * v_3d;
  // 应该显式转换
  Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;
  cout << "[1,2,3;4,5,6]*[3,2,1]=" << result.transpose() << endl;

  Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;
  cout << "[1,2,3;4,5,6]*[4,5,6]: " << result2.transpose() << endl;

  // 同样你不能搞错矩阵的维度
  // 试着取消下面的注释，看看Eigen会报什么错
  // Eigen::Matrix<double, 2, 3> result_wrong_dimension = matrix_23.cast<double>() * v_3d;

  // 一些矩阵运算
  // 四则运算就不演示了，直接用+-*/即可。
  matrix_33 = Matrix3d::Random();      // 随机数矩阵
  cout << "random matrix: \n" << matrix_33 << endl;
  cout << "transpose: \n" << matrix_33.transpose() << endl;      // 转置
  cout << "sum: " << matrix_33.sum() << endl;            // 各元素和
  cout << "trace: " << matrix_33.trace() << endl;          // 迹
  cout << "times 10: \n" << 10 * matrix_33 << endl;               // 数乘
  cout << "inverse: \n" << matrix_33.inverse() << endl;        // 逆
  cout << "det: " << matrix_33.determinant() << endl;    // 行列式

  // 特征值
  // 实对称矩阵可以保证对角化成功
  SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33);
  cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
  cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;

  // 解方程
  // 我们求解 matrix_NN * x = v_Nd 这个方程
  // N的大小在前边的宏里定义，它由随机数生成
  // 直接求逆自然是最直接的，但是求逆运算量大

  Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN
      = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
  matrix_NN = matrix_NN * matrix_NN.transpose();  // 保证半正定
  Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);

  clock_t time_stt = clock(); // 计时
  // 直接求逆
  Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd;
  cout << "time of normal inverse is "
       << 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;
  cout << "x = " << x.transpose() << endl;
 // 对于正定矩阵，还可以用cholesky分解来解方程
  time_stt = clock();
  x = matrix_NN.ldlt().solve(v_Nd);
  cout << "time of ldlt decomposition is "
       << 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;
  cout << "x = " << x.transpose() << endl;

  return 0;

实践结果如下：（运行代码就是简单 mkdir build; cd build; cmake .. ; make ; ./useEigen）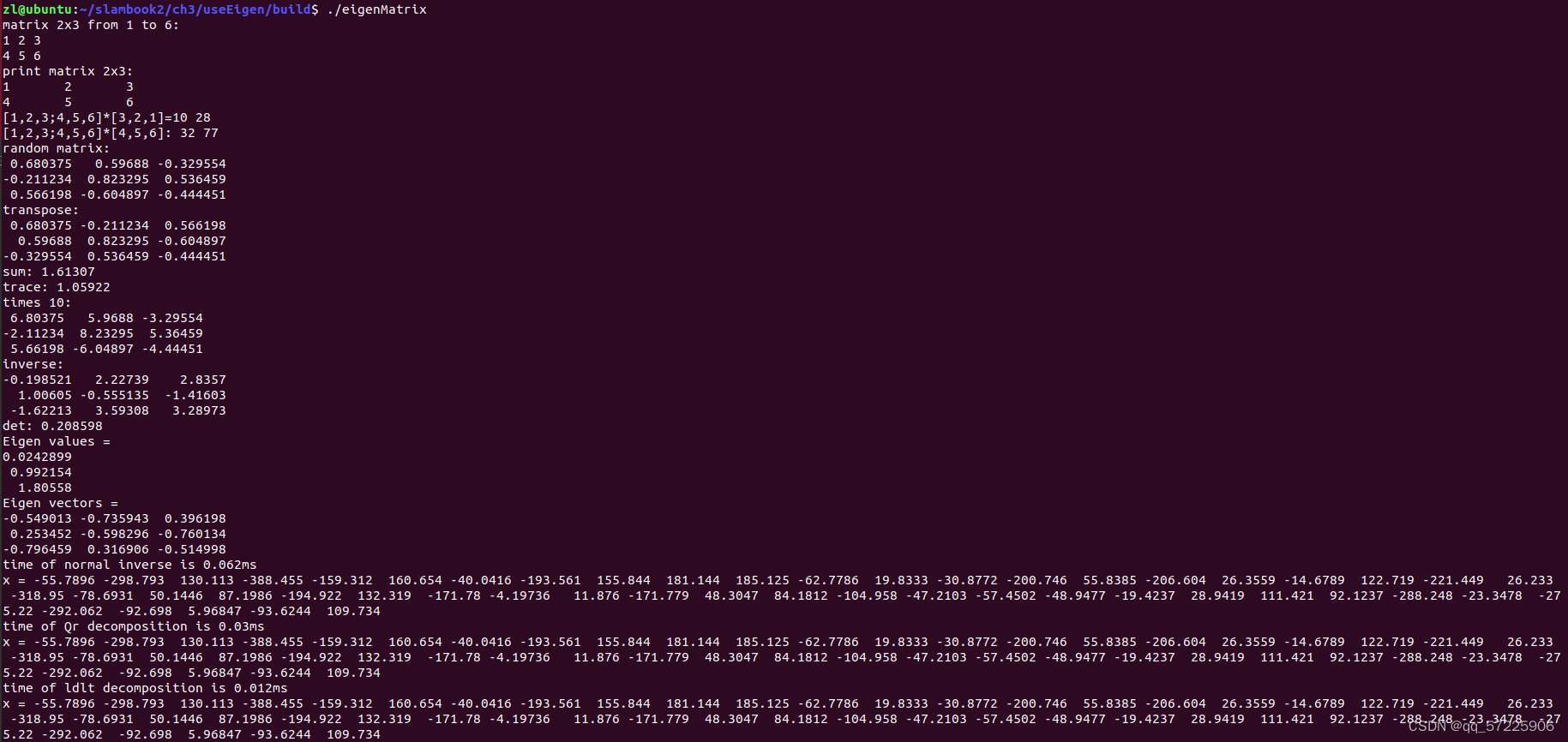

Eigen库中的Geometry模块包含了矩阵、向量表达和运算，提供了几何方面的知识。ch3中的useGeometry.cpp对Geometry模块进行了简单应用，代码如下：

#include <iostream>
#include <cmath>

using namespace std;

#include <Eigen/Core>
#include <Eigen/Geometry>

using namespace Eigen;

// 本程序演示了 Eigen 几何模块的使用方法

int main(int argc, char **argv) {

  // Eigen/Geometry 模块提供了各种旋转和平移的表示
  // 3D 旋转矩阵直接使用 Matrix3d 或 Matrix3f
  Matrix3d rotation_matrix = Matrix3d::Identity();
  // 旋转向量使用 AngleAxis, 它底层不直接是Matrix，但运算可以当作矩阵（因为重载了运算符）
  AngleAxisd rotation_vector(M_PI / 4, Vector3d(0, 0, 1));     //沿 Z 轴旋转 45 度
  cout.precision(3);
  cout << "rotation matrix =\n" << rotation_vector.matrix() << endl;   //用matrix()转换成矩阵
  // 也可以直接赋值
  rotation_matrix = rotation_vector.toRotationMatrix();
  // 用 AngleAxis 可以进行坐标变换
  Vector3d v(1, 0, 0);
  Vector3d v_rotated = rotation_vector * v;
  cout << "(1,0,0) after rotation (by angle axis) = " << v_rotated.transpose() << endl;
  // 或者用旋转矩阵
  v_rotated = rotation_matrix * v;
  cout << "(1,0,0) after rotation (by matrix) = " << v_rotated.transpose() << endl;

  // 欧拉角: 可以将旋转矩阵直接转换成欧拉角
  Vector3d euler_angles = rotation_matrix.eulerAngles(2, 1, 0); // ZYX顺序，即yaw-pitch-roll顺序
  cout << "yaw pitch roll = " << euler_angles.transpose() << endl;

  // 欧氏变换矩阵使用 Eigen::Isometry
  Isometry3d T = Isometry3d::Identity();                // 虽然称为3d，实质上是4＊4的矩阵
  T.rotate(rotation_vector);                                     // 按照rotation_vector进行旋转
  T.pretranslate(Vector3d(1, 3, 4));                     // 把平移向量设成(1,3,4)
  cout << "Transform matrix = \n" << T.matrix() << endl;

  // 用变换矩阵进行坐标变换
  Vector3d v_transformed = T * v;                              // 相当于R*v+t
  cout << "v tranformed = " << v_transformed.transpose() << endl;

  // 对于仿射和射影变换，使用 Eigen::Affine3d 和 Eigen::Projective3d 即可，略

  // 四元数
  // 可以直接把AngleAxis赋值给四元数，反之亦然
  Quaterniond q = Quaterniond(rotation_vector);
  cout << "quaternion from rotation vector = " << q.coeffs().transpose()
       << endl;   // 请注意coeffs的顺序是(x,y,z,w),w为实部，前三者为虚部
  // 也可以把旋转矩阵赋给它
  q = Quaterniond(rotation_matrix);
  cout << "quaternion from rotation matrix = " << q.coeffs().transpose() << endl;
  // 使用四元数旋转一个向量，使用重载的乘法即可
  v_rotated = q * v; // 注意数学上是qvq^{-1}
  cout << "(1,0,0) after rotation = " << v_rotated.transpose() << endl;
  // 用常规向量乘法表示，则应该如下计算
  cout << "should be equal to " << (q * Quaterniond(0, 1, 0, 0) * q.inverse()).coeffs().transpose() << endl;

  return 0;
}
~

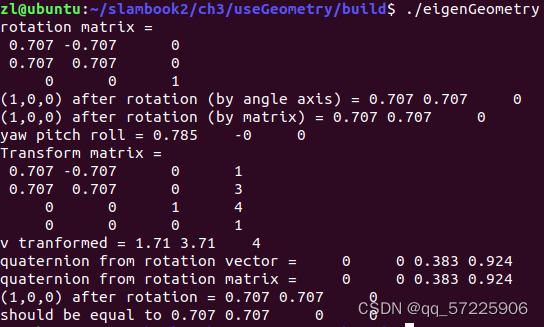
代码运行结果如下：