目录
通过Sin函数加入噪声干扰后,利用多项式去拟合的例子进行说明
工大菜凯,希望通过做笔记记录自己学的知识,也希望能帮助到同样在入门的同学 ❥侵权立删~
统计学习方法第一章
最小二乘法拟合曲线的基本概念
总结一下:最小二乘法主要就是为了找到一组参数,使得系统的平方损失函数最小化。
通过Sin函数加入噪声干扰后,利用多项式去拟合的例子进行说明
最小二乘法的实践
我们用目标函数y=sin2πx,加上一个正态分布的噪声干扰,然后我们用多项式去拟合它。
import numpy as np
import scipy as sp
from scipy.optimize import leastsq # leastsq 最小二乘拟合函数
import matplotlib.pyplot as plt# 目标函数 sin2πx
def real_func(x):
return np.sin(2*np.pi*x)
# 拟合函数 利用np.polyld 去生成p阶多项式 多项式的自变量是x
# 举例说明:numpy.poly1d([1,2,3]) 生成 𝑥^2+2𝑥^1+3𝑥^0
def fit_func(p, x):
f = np.poly1d(p)
return f(x)
# 残差函数 求解拟合函数与真实标签值y之间的差距
def residuals_func(p, x, y):
ret = fit_func(p, x) - y
return ret# 在[0,1]之间生成10个等间距的点 间距为0.1
x = np.linspace(0, 1, 10)
# 在[0,1]之间生成1000个等间距的点 间距为0.001
x_points = np.linspace(0, 1, 1000)
# 对目标函数sin2πx 加入正态分布的噪声干扰 (np.random.normal(0, 0.1)+y1 利用np库生成一个均值为0,# 标准差为0.1的正态分布,并在这个正态分布中任意选择一个数,加到目标函数的y_real上,产生噪声干扰)
# for y1 in y_real 取y_real中的每一元素给y1
y_real = real_func(x)
y = [np.random.normal(0, 0.1)+y1 for y1 in y_real]
# 定义拟合多项式,其中参数M为多项式的次数
def fitting(M=0):
# np.random.rand() 是 NumPy 库中用于生成服从均匀分布的随机数的函数。
# 它返回一个或多个在 [0, 1) 范围内均匀分布的随机样本。
p_init = np.random.rand(M+1) # 生成M+1个[0,1)范围内均匀分布的随机数,作为多项式的参数
# M+1=1 代表的是0阶多项式 也就是 p_init+0*x+0*x^2...... 0阶多项式,产生的系数个数为1
# 最小二乘法
p_lsq = leastsq(residuals_func, p_init, args=(x, y))
# residuals_func 是待最小化的残差函数 , p_print是待优化多项式的的初始参数值
# p_print 会自动为residuals_func 函数匹配输入参数p的值
# args=(x, y)为残差函数传递 输入向量x 和 观测向量(真实标签)y_real
# 求解出来的p_lsp值 就是在该M阶数多项式中,最小二乘法拟合曲线的最优系数,在这个最优系数下的M多项式可以更好的拟合真实标签y,使得其平方损失函数最小
print('Fitting Parameters:', p_lsq[0])
# 可视化
plt.plot(x_points, real_func(x_points), label='real') # 绘画没加噪声干扰的sin2πx的曲线
# 绘画通过最小二乘法优化参数后的拟合函数曲线
plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve')
# 绘画加入(0,0.1)正态分布干扰后的sin图像 噪声点 bo绘画散点图的参数 , b:bule o:圆圈
plt.plot(x, y, 'bo', label='noise')
plt.legend()
return p_lsq# M=0
p_lsq_0 = fitting(M=0)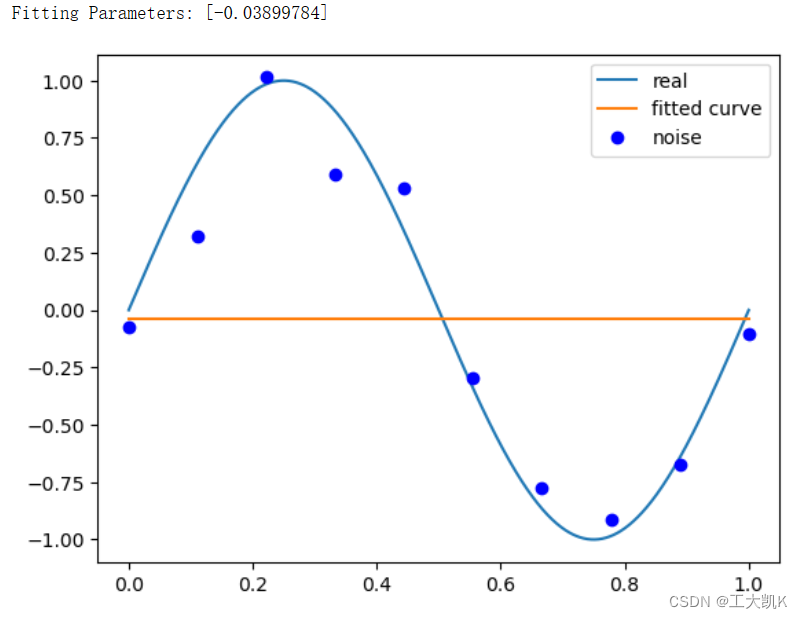
# M=1
p_lsq_1 = fitting(M=1)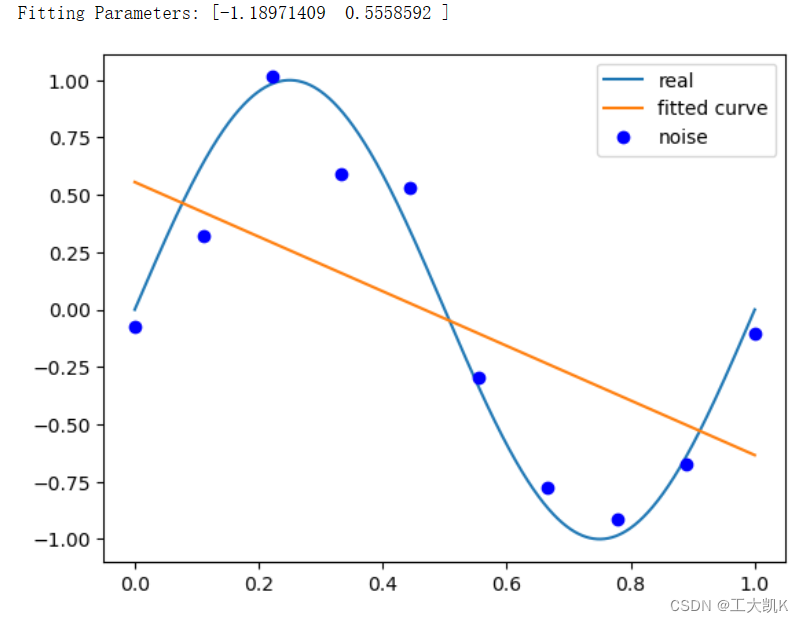
# M=3
p_lsq_3 = fitting(M=3)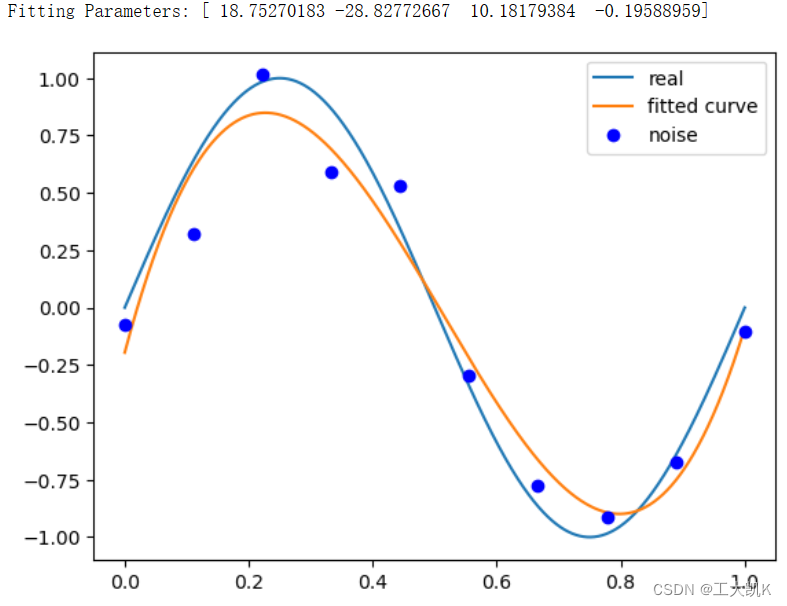
# M=9
p_lsq_9 = fitting(M=9)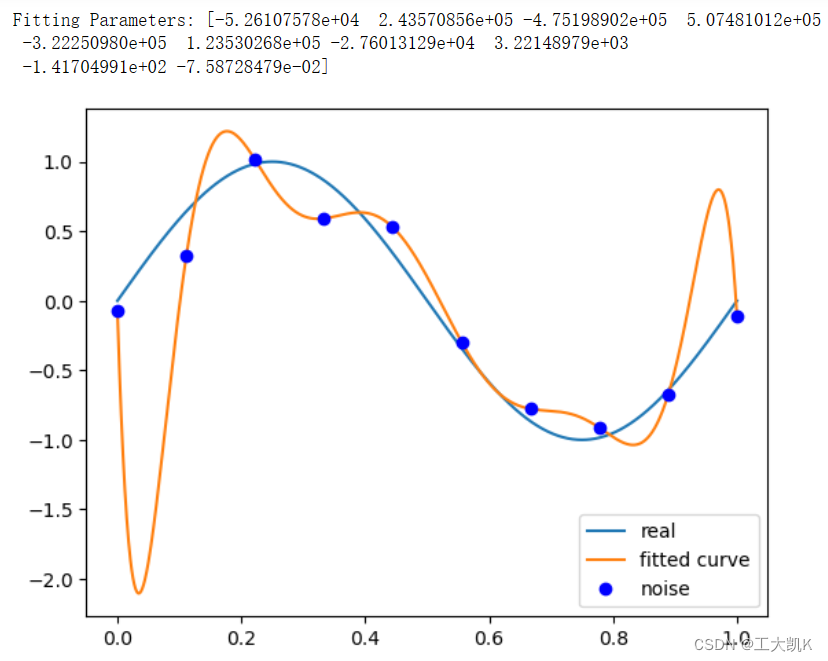
总结:
当M=9时,多项式曲线通过了每个数据点,但是造成了过拟合现象。接下来我们通过最常见的引入正则化项,来降低过拟合现象。
正则化方法(降低过拟合现象)
上面结果显示过拟合, 引入正则化项(regularizer),降低过拟合现象
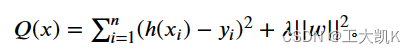
回归问题中,损失函数是平方损失函数,正则化可以是参数向量的L2范数,也可以是L1范数。
其中:W就是上面最小二乘法求出来的最优系数
-
L1范数: regularization(正则化系数:lambda)*abs(p)
-
L2范数: 1/2 * regularization(正则化系数:lambda) * np.square(p)
regularization = 0.0001 # 正则化系数
# 正则化的残差函数
def residuals_func_regularization(p, x, y):
ret = fit_func(p, x) - y # 没有加正则化项的最小二乘法的残差数组
ret = np.append(ret, 0.5*regularization*np.square(p)) # 在数组的后面加上正则化L2范数
# 在最小二乘法的残差数组中添加 L2范数 作为正则化项
# 相当于现在的ret=[ret,0.5*regularization*np.square(p)]
return ret# 最小二乘法+正则化项
p_init = np.random.rand(9+1) #相当于随机的在[0,1]内选10个数,作为9阶多项式的初始参数,下面应用后就默认生成9阶多项式
p_lsq_regularization = leastsq(residuals_func_regularization, p_init, args=(x, y))# 生成sin2πx的图像
plt.plot(x_points, real_func(x_points), label='real')
# 生成未加入正则化L2范数的最小二乘法的9阶多项式拟合函数图像
plt.plot(x_points, fit_func(p_lsq_9[0], x_points), label='fitted curve')
# 生成加入正则化L2范数的最小二乘法的9阶多项式拟合图像
plt.plot(x_points, fit_func(p_lsq_regularization[0], x_points), label='regularization')
plt.plot(x, y, 'bo', label='noise')
plt.legend()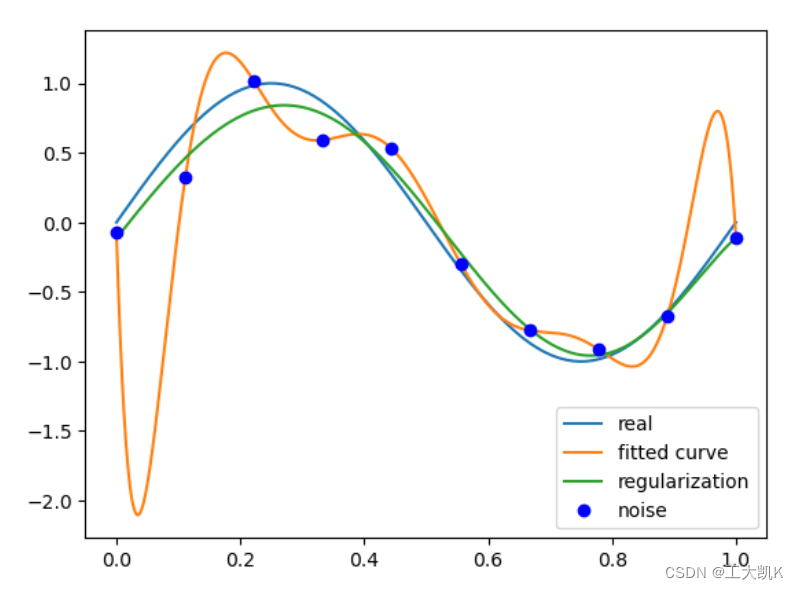
补充:matplotlib库中函数的使用


























 1117
1117











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










