谐波响应：理论基础与基本操作

目录

一、什么是谐波响应

1.1 基本定义

1.2 关键问题

二、谐波响应的数学基础

2.1 单自由度系统的谐波响应

(1)稳态解

(2)幅值和相位

2.2 多自由度系统的谐波响应

三、谐波响应案例分析

步骤1：在模态分析的基础上建立谐波响应系统

步骤2： 载荷设置

步骤3：分析器设置 

步骤4：结果后处理

---

一、什么是谐波响应

1.1 基本定义

谐波响应（Harmonic Response）是指结构在周期性简谐载荷（如正弦波激励）作用下的稳态振动响应。

• 简谐载荷：载荷随时间按正弦或余弦规律变化，例如：

1.2 关键问题

谐波响应分析要回答：

• 当结构受到某个频率的周期性载荷时，它的振幅有多大？

• 结构的振动相位相对于激励是否有延迟？

• 在哪些频率下会发生共振？

二、谐波响应的数学基础

2.1 单自由度系统的谐波响应

对于一个单自由度系统（如弹簧-质量-阻尼系统），其运动方程为：

(1)稳态解

稳态解的形式为：

(2)幅值和相位

响应的幅值和相位可以通过以下公式计算：

2.2 多自由度系统的谐波响应

对于多自由度系统，运动方程可以写成矩阵形式：

通过模态分析，可以将多自由度系统解耦为多个单自由度系统，然后分别求解每个模态的谐波响应，最后叠加得到总响应。 

三、谐波响应案例分析

步骤1：在模态分析的基础上建立谐波响应系统

模态分析：音叉不同状态下的模态-CSDN博客

将谐波响应项目Harmonic Response拖拽到模态分析Modal的第六个框求解solution的位置

步骤2： 载荷设置

步骤3：分析器设置 

模态分析器设置：

谐波响应分析器设置：

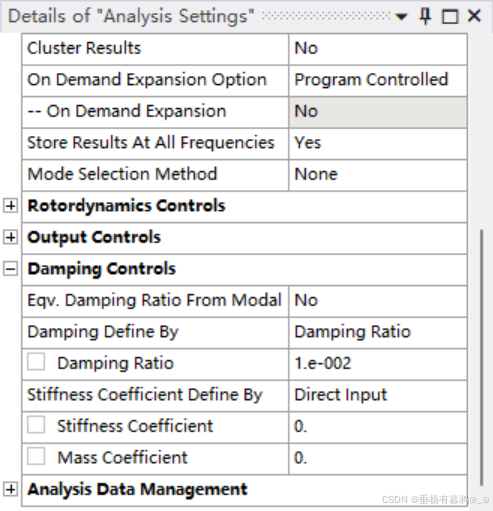
步骤4：结果后处理

关键结构项：

• 总变形 (Total Deformation)

• 频率响应(Frequency Response)

 节点选择