[leetcode](剑指offer) 最长公共子序列

follow the wind26

已于 2022-11-02 00:04:46 修改

阅读量612

点赞数

分类专栏： # 动态规划文章标签： leetcode 算法职场和发展

于 2022-11-02 00:00:09 首次发布

本文链接：https://blog.csdn.net/qq_59214888/article/details/127601165

版权

动态规划专栏收录该内容

2 篇文章 0 订阅

订阅专栏

思路来源：

leetcode官网解答帖

最长公共子序列 (LCS) 详解+例题模板（全）

https://leetcode.cn/problems/qJnOS7/solution/zui-chang-gong-gong-zi-xu-lie-by-leetcod-ugg7/

https://blog.csdn.net/lxt_Lucia/article/details/81209962

问题描述：

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

问题分析：

1.暴力求解

首先考虑暴力解法，如果使用暴力解法，需要则解决2个问题：

1.如何确定子序列划分的长度？

2.如何在序列中检测划分的子序列而且还得是最长的？

为什么要划分子序列的长度？可以观察题目中的举例，"ace"是"abcde"的子序列，而且是删除了两个中间值后形成的，那么是否可以设置下标指针将字符串的某些中间值删除呢？答案是不行，因为在示例中，"abcde"删除的是第二个和第四个元素，如果有一个字符串删除了第二个和第四，第五个元素那会怎么样呢，结果就是子序列检测长度L,要发生变化，而要从原始字符串中形成子序列至少需要三层循环，一层控制L的大小，一层确定子序列的开始下标start，最后一层来确定检测序列长度的开始位置Lstart，如果L的大小还需要不断地变化那么需要再设置一层循环来控制其变换后的大小，这样就需要四层循环，会使本就低效的算法雪上加霜，因此首先舍弃掉这种不靠谱的方法。（如何划分连续子序列可以参考下面的文章中的暴力解法一和二，里面简单说明了对连续子序列的划分。）

https://blog.csdn.net/qq_59214888/article/details/127585609?spm=1001.2014.3001.5501

那就不考虑划分长度检测了，直接挨个检测。题目中会给两个字符串text1和text2，可以在text1中挨个检测text2的元素，有一个算一个。但是，如果考虑元素的顺序那么就需要设置判断条件，而且如果text2中有重复的值该怎么办呢？（貌似需要保存第一次查找重复元素的地址）这个算法理论上可以实现。

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2)
    {
        size_t subindex=0;
        int max=0;
        for(char i:text2)
        {
            size_t test=text1.find(i,subindex);
            if(test!=-1)
            {
                subindex=test+1;
                max++;
                continue;
            }
        }
        return max;
    }
};

可以注意到根据上面的代码只会进行一次的迭代并不会对所有的元素都进行迭代，例如text2="shmtulqrypy",text1="oxcpqrsvwf",上述代码只会在text1中匹配's'后面的元素，会输出1，然而真正的最长公共子序列是“qp”。下面的代码是对这个问题的改进。

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2)
    {
        size_t subindex=0;
        int max=0;
        for(string::iterator i=text2.begin();i!=text2.end();i++)
        {
            int visiallength=0;
            for(string::iterator j=i;j!=text2.end();j++)
            {
                char content=*j;
                size_t test=text1.find(content,subindex);
                if(test!=-1)
                {
                    subindex=test+1;
                    visiallength++;
                    if(visiallength>max)
                    {
                        max=visiallength;
                    }
                    continue;
                }
            }
            subindex=0;
            visiallength=0;
        }
        return max;
    }
};

通过双重迭代器，实现了对每一个元素的迭代循环，但是上述代码还是存在问题，其中问题是这样的：

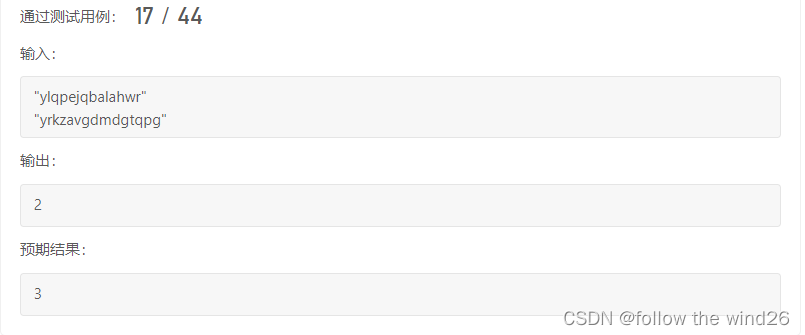
可以观察到在第二个字符串text2=“yrkzavgdmdgtqpg”与text1="ylqpejqbalahwr"中在迭代text2中的‘r’字符时在text1中指针会匹配到最后，因此会跳过‘qp’字符，输出2，然而真正的最大字符串为“yqp”。即便如此，也不对上述代码进一步改进，因为要实现这个功能就要再加入一层循环来迭代除了Lstart剩下的字符，然而在这个题目中，text1与text2的值都可以达到1000，因此就算是改进完成依旧无法通过测试。

2.动态规划

似乎这个问题可以被划分成不同的子问题来解决，为什么这么说？为什么要划分子问题？如果可以那应该划分成什么样的子问题呢？要解决动态规划问题就需要建立合适的数学模型来抽象问题，因此选择合适的角度分析问题是十分关键的。在本题中可以分别建立多个小的数学模型，也就是说需要试着使用数学语言来描述问题（这个过程并不需要在乎模型是否正确，只需要尝试建立模型即可）。

回到刚才的提问上面，似乎总的问题并不好划分为子问题，但是可以将字符串划分为不同的子字符串，并且设置一个函数来表示这些子字符串的最长公共子序列的长度。因此，令 $text1[0:i]$ 为 $text1$ 的子字符串记为 $text1_{i}$ ，令 $text2[0:j]$ 为 $text2$ 的子字符串记为 $text2_{j}$ ，令 $p(text1_{i},text2_{j}),i=0,1,...,text1.length,j=0,1,...,text2.length$ 为 $text1~and~text2$ 各子序列的长度，那么 $max(p(text1,text2))$ 就是所要求的最大的公共子序列的长度，然而这个模型并不能实质性解决，因为本来就是需要求解子序列，把问题分成小问题依旧需要求解子序列，其中存在类 $max(p(text1_{i+1},text2_{j+1})))>=max(p(text1_{i},text2_{j})))$ 的关系。然而这个判断的条件在刚才的求解中存在着问题，所以需要建立新的数学模型来抽象问题。

1.来自leetcode官网的解答：

令 $text1 ~and ~text2$ 为两个待测试字符串，其中 $text1\left[~\text{i}~\right]$ 表示 $text1$ 字符串中的第 $i+1$ 个字符，同理 $text2\left[~\text{j}~ \right ]$ 表示 $text2$ 字符串中的 $j+1$ 个字符，并且令 $text1\left[~\text{0:i}~ \right ]$ 表示 $text1$ 中长度为 $i$ 的前缀， $text2\left[~\text{0:j} ~\right ]$ 表示 $text2$ 中长度为 $j$ 的前缀。建立 $dp\left[~i~ \right ]\left[~j~\right]$ 表示 $text1\left[~0:i~\right]$ 和 $text2\left[~0:j~ \right ]$ 的最长公共子序列的长度。

动态规划的边界情况：

1.当 $i=0$ 时， $text1[0:i]$ 为空，空字符串和任何字符串的最长公共子序列的长度都是0，因此对任意 $0 \le j\le n$ ,有 $dp[0][j]=0;$

2.当 $j=0$ 时， $text2[0:j]$ 为空，同理可得，对任意 $0\le i\le m$ ,有 $dp[i][0]=0;$

3.当 $i>0,j>0$ 时：

3.1 当 $text1[i-1]=text2[j-1]$ 时，考虑 $text1[0:i-1]$ 和 $text2[0:j-1]$ 的最长公共子序列，再增加一个公共字符即可得到 $text1[0:i]$ 和 $text2[0:j]$ 的最长公共子序列，因此 $dp[i][j]=dp[i-1][j-1]+1$

3.2 当 $text1[i-1]\neq text2[j-1]$ 时，应该考虑两项， $text1[0:i-1],text2[0:j]$ 的最长公共子序列以及 $text1[0:i],text2[0:j-1]$ 的最长公共子序列（为什么要考虑 $text1[0:i-1]$ 而不是 $text1[0:i-2]$ 或者 $text1[0:i-n]$ 呢？因为在剩余的前缀和序列中 $text1[0:i-1]$ 是最大的，从之前的定义来看 $text1[0:i-1]$ 会包含其他几种前缀和在其中，因此状态转移方程dp的结果是最全的。）

状态转移方程为：

$dp[i][j]=\left\{ \begin{array}{ll} dp[i-1][j-1]+1,~~~~~~~~~~~~~~text1[i-1]=text2[j-1]\\ max(dp[i-1][j],dp[i][j-1]),~text1[i-1]\neq text2[j-1] \end{array} \right.\\$

边界条件初始化：

vector<vector<int>> dp(text1.length()+1,vector<int>(text2.length()+1));
        //初始化边界条件
        for(int i=0;i<=text1.length();i++)
        {
            dp[i][0]=0;
        }
        for(int j=0;j<=text2.length();j++)
        {
            dp[0][j]=0;
        }

状态转移过程：

//注意这里的i，j都从1开始迭代,否则会下标会超出范围
//并且i要最后等于text1的长度，j也要最后等于text2的长度，否则迭代到最后一个dp元素
for(int i=1;i<=text1.length();i++)
{
    for(int j=1;j<=text2.length();j++)
    {
        //注意字符串下标与状态转移矩阵dp的下标并不一致，dp下标从1开始到n结束，而字符串下标从0开 
        //始到n-1结束，这样做可以确保text字符串与dp矩阵都可以遍历一遍
        if(text1[i-1]==text2[j-1])
        {
            //dp矩阵有提前进行元素赋值的性质
            dp[i][j]=dp[i-1][j-1]+1;
        }
        else
        {
            dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
        }
    }
}

完整代码：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) 
    {
        vector<vector<int>> dp(text1.length()+1,vector<int>(text2.length()+1));
        //初始化边界条件，创建矩阵时自动初始化，这一步没有必要
        for(int i=0;i<=text1.length();i++)
        {
            dp[i][0]=0;
        }
        for(int j=0;j<=text2.length();j++)
        {
            dp[0][j]=0;
        }
        //状态转移
        for(int i=1;i<=text1.length();i++)
        {
            for(int j=1;j<=text2.length();j++)
            {
                if(text1[i-1]==text2[j-1])
                {
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else
                {
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[text1.length()][text2.length()];
    }
};

注意：dp矩阵的下标比text字符串的下标大1；

2.来自CSDN博客的解答

https://blog.csdn.net/lxt_Lucia/article/details/81209962