数与图的深度优先搜索、宽度优先搜索、拓扑序列（邻接矩阵、邻接表）

数据结构中，对于图的存储我们是使用邻接矩阵或者邻接表来进行存储的。树就是一种特殊的图，而图我们又分为有向图和无向图，而无向图又是一种特殊的有向图，即每两点之间都存在两条通路。
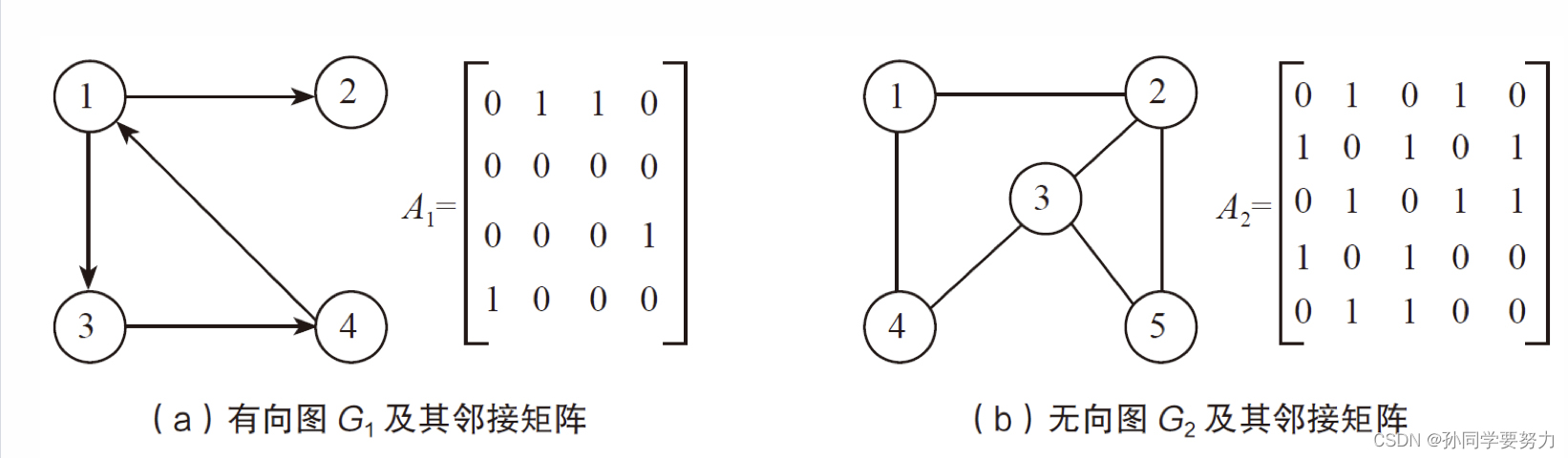
邻接矩阵存储，是指用一个一维数组存储图中顶点的信息，用一个二维数组存储图中边的信息，即各顶点之间的邻接关系，存储顶点之间邻接关系的二维数组称为邻接矩阵。用的很少，我们重点要掌握邻接表。

临接矩阵

不带权邻接矩阵中，A[i][j] = 1代表两点之间临接；A[i][j] = 0代表两点不临接

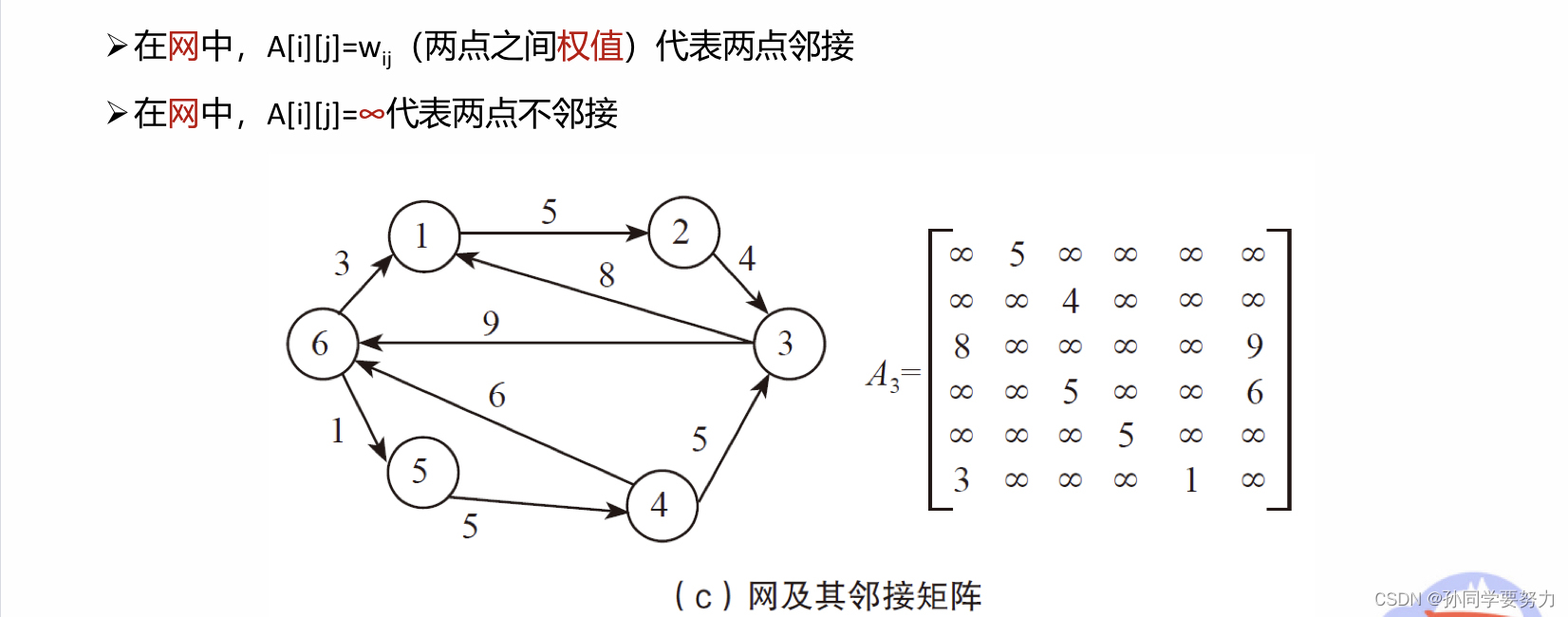
带权的邻接矩阵中：
A[i][j] = wij（两点之间的权值）代表两点邻接
A[i][j] = ∞ 代表两点不相邻

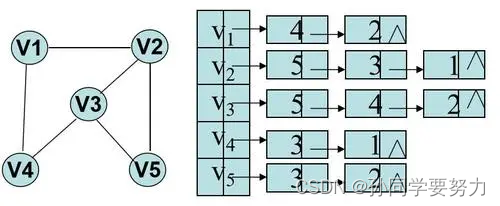
邻接表的存储，如果有n个顶点，我们就开辟n个单链表，每个链表表示顶点可以到那些点。

树与图的深度优先遍历

邻接表的存储

int h[N], e[N * 2], ne[N * 2], idx;

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

树和图的dfs模板

void dfs(int u)
{
	state[u] = true;//标记一下，记录已经被搜索过了
	for(int i = h[i]; i != -1; i = ne[i])
	{
		int j = e[i];
		if(!state[j]) dfs(j);
	}
}

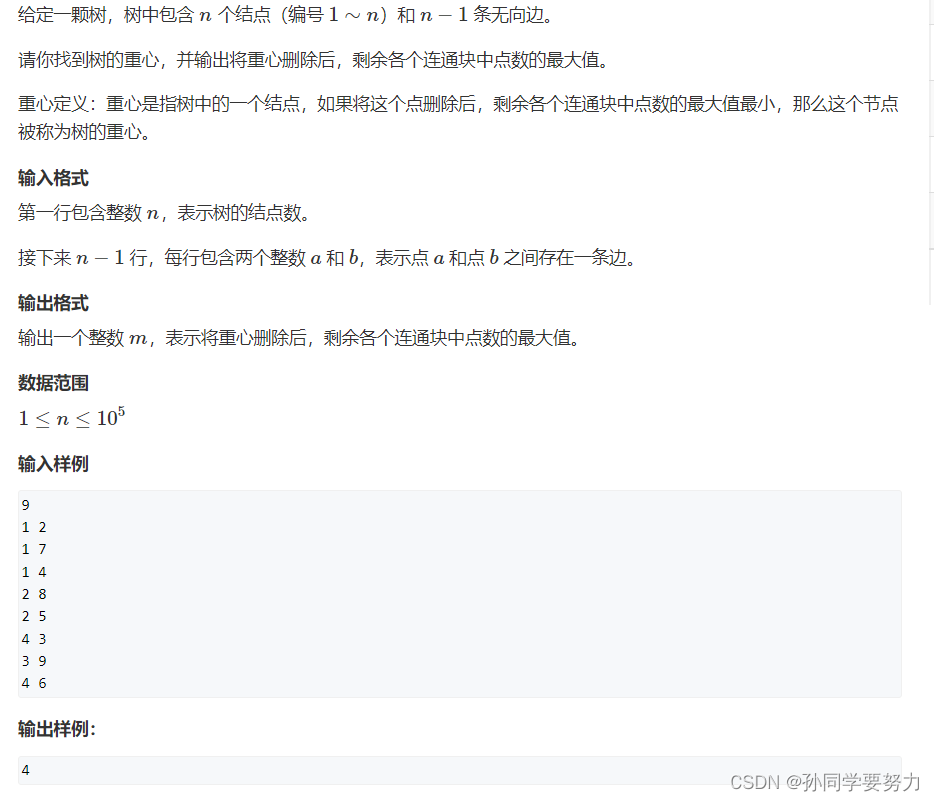
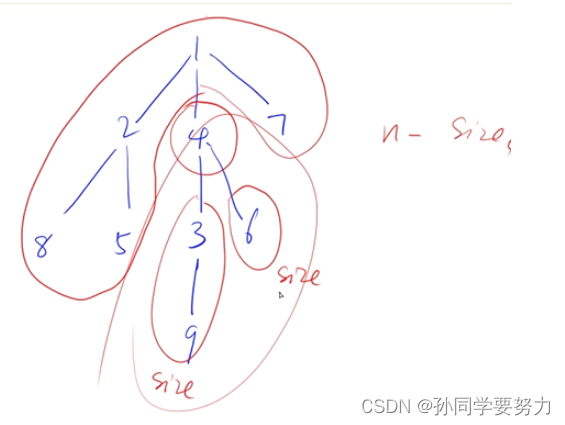
我们要求删除一个节点u后最大联通快的大小，我们会分割成三个联通块
即

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int n;
int h[N], e[N * 2], ne[N * 2], idx;//n个单链表
bool state[N];//表示该节点是否遍历过
int ans = N;//最终的答案

void add(int a, int b)//在节点a上加一条到b的边
{
    e[idx] = b;
    ne[idx] = h[a]; 
    h[a] = idx++;
}

int dfs(int u)
{
    state[u] = true;//进来先标记一下该节点已经遍历过了
    
    int size = 0;//size表示将u去除后，剩余子树中连通块的最大值
    int sum = 1;//sum表示以u为根的子树的点有多少，初始值为1，因为已经有这个根了
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!state[j])
        {
            int s = dfs(j);//s是以j为根节点的子树中节点的数量
            size = max(size, s);
            sum += s;
        }
    }
    size = max(size, n - sum);
    ans = min(size, ans);
    return sum;
}

int main()
{
    scanf("%d", &n);
    
    memset(h, -1, sizeof h);//把每个节点的链表都初始化为-1，即刚开始的节点链表都是空链表，指向-1
    
    for(int i = 0; i < n - 1; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);//因为是无向边，所以每两个节点之间都有两条边
    }
    
    dfs(1);//从第一个节点开始搜索，从那个节点搜索都是可以的
    
    cout << ans << endl;
    
    return 0;
}

树与图的广度优先遍历

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], e[N], ne[N], idx;
int d[N];//表示到节点1的距离是多少

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int bfs()
{
    memset(d, -1, sizeof d);
    
    queue<int> q;
    d[1] = 0;
    q.push(1);
    
    while(q.size())
    {
        int t = q.front();
        q.pop();
        
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(d[j] == -1)//j没有被扩展过
            {
                d[j] = d[t] + 1;
                q.push(j);
            }
        }
    }
    return d[n];
}

int main()
{
    scanf("%d%d", &n, &m);
    
    memset(h, -1, sizeof h);
    
    for(int i = 0; i < m; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }
    
    cout << bfs() << endl;
    
    return 0;
}

拓扑序列

拓扑序列是基于有向无环图的：拓扑序列只有从前指向后的边，没有从后指向前的边，即入度为0
入度：指被指向边的数量
初度：指指向边的数量

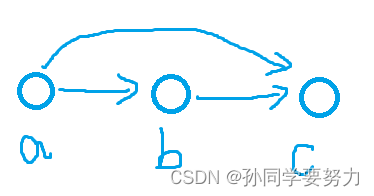
如图：a的入度为0，出度为2
如图就是一个拓扑结构；注意：只要一个图构成了了环就一定不是拓扑结构
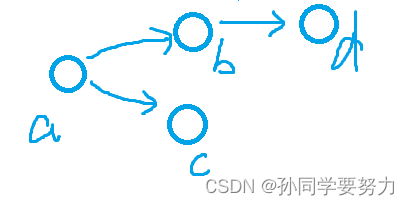
拓扑序列的输出可以有多种形式：

如图：输出的方式可以是：a,b,c,d; 也可以是：a,c,b,d; 也可以是：a,b,d,c
我们可以发现入队的点是顺序的就是拓扑结构，所有的边都是从前指向后的
求拓扑结构就是把入度为0的点都排到前面去
有向无环图就是拓扑图

例题：

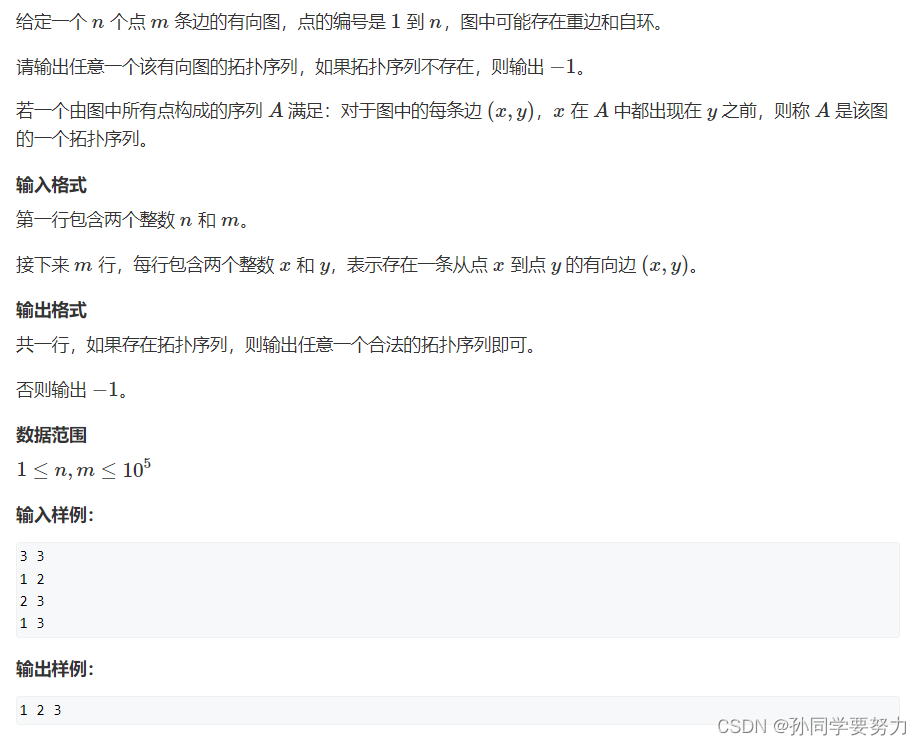
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], e[N], ne[N], idx;
int q[N];//表示队列
int d[N];//表示到起点的距离，深度

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

bool topsort()
{
    int hh = 0, tt = -1;//初始化队列
    for(int i = 1; i <= n; i++)
    {
        if(!d[i]) q[++tt] = i;//将入度为0的点入队
    }
    while(hh <= tt)//队列不为空
    {
        int t = q[hh++];//取出队头
        for(int i = h[t]; i != -1; i = ne[i])//遍历邻接表
        {
            int j = e[i];
            d[j]--;//删除点t指向点j的边
            if(d[j] == 0) //如果点j的入度为0了，就将j入度
                q[++tt] = j;
        }
    }
    
    return tt == n - 1;//如果n个点都入队了的话，就说明该图是拓扑结构
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);//先把邻接表的每个点都置成空的，即初始化邻接表
    for(int i = 0; i < m; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
        d[b]++;//因为a指向b所以b点的深度要加1
    }
    if(topsort())
    {
        for(int i = 0; i < n; i++) printf("%d ", q[i]);
        puts("");
    }
    else puts("-1");
    
    return 0;
}