六、流形优化-CSDN博客

本文链接：https://blog.csdn.net/qq_60073245/article/details/147704316

背景

在实际情况下，我们需要处理3D旋转和其他非线性流形，在三维流形上，我们并不能直接采用方法去优化它，这些需要更复杂的机器来考虑它们的特殊结构。书中举了一个例子来说明这个问题，我们来看看这个例子。

假设我们可以访问一个加速度计，该加速度计除了重力之外不受任何力的影响，并输出三维测量值za ∈ R 3。此外，我们假设我们可以访问以下测量函数，该函数根据旋转R预测加速度计测量值za：

$h^a:SO(3)\to\mathbb{R}^3:R\mapsto z_a$

性质：三维旋转矩阵 R∈SO(3) 必须满足正交性（R⊤R=I）和行列式为1（det⁡(R)=1）。

尝试通过最小化最小二乘误差准则来估计未知旋转R，最小化预测与测量的误差：

$R^{*}=\underset{R}{\operatorname*{\mathrm{argmin}}}\|h^{a}(R)-z_{a}\|_{\Sigma}^{2}$

若在三维旋转流形（SO(3)）直接使用向量空间优化方法：

$R_{\mathrm{new}}=R_0+\xi$

这里R0是三维单位矩阵，ξ是3×3增量矩阵。

这时及时ξ是微小增量，也会使得 Rnew 的列向量不再正交，且行列式可能不等于1，导致其不再属于SO(3)。这里运用了李代数与指数映射方法来解决这个问题。

在介绍李代数与指数映射方法前，我们先介绍一下轴角表示法和反对称矩阵它是连接李代数与李群的关键步骤，为指数映射奠定了基础。

轴角表示法

任何三维旋转可表示为旋转轴 ωˉ∈S2（单位球面）和旋转角度 θ 的组合。两者结合为一个三维向量，同时编码旋转轴与角度信息。

当 θ 较小时，旋转矩阵可近似为 $R(\xi)\approx I+\hat{\xi}$

$\left.R(\xi)\approx\left[ \begin{array} {ccc}1 & -\xi_z & \xi_y \\ \xi_z & 1 & -\xi_x \\ -\xi_y & \xi_x & 1 \end{array}\right.\right]$

李代数元素(反对称阵)：

$\hat{\xi}= \begin{bmatrix} 0 & -\xi_z & \xi_y \\ \xi_z & 0 & -\xi_x \\ -\xi_y & \xi_x & 0 \end{bmatrix}$

指数映射可将李代数转换为李群，在详细介绍指数映射前，我们先来看看这俩的概念。

李群：代表具有连续对称性的几何结构，例如：
- SO(3)：三维旋转矩阵的集合。
- SE(3)：三维刚体变换（旋转+平移）的集合。
- SO(2)：二维旋转矩阵的集合。
这些群中的元素（如旋转矩阵）必须满足严格的几何约束（如正交性、行列式为1），但直接优化这些元素会导致复杂约束问题。
李代数：对应李群的“切空间”（局部线性空间），例如：
- so(3)：三维旋转对应的反对称矩阵集合。
- se(3)：三维刚体变换对应的矩阵集合。
李代数是向量空间，其元素（如三维向量）可以自由加减，无需考虑约束。

李代数将非线性流形上的优化问题转换为向量空间中的无约束问题，简化计算。通过指数映射，增量操作始终生成合法的李群元素。

指数映射

指数映射通过闭合形式确保任意大小的旋转均生成合法的旋转矩阵，完全满足正交性和行列式为1的约束。

闭合表达式：对于任意三维向量，指数映射可简化为：

$\exp(\hat{\xi})=I+\frac{\sin\theta}{\theta}\hat{\xi}+\frac{1-\cos\theta}{\theta^2}\hat{\xi}^2$

第一项 I 对应无旋转的初始状态。
第二项 (sin⁡θ/θ)ξ 描述旋转的线性部分。
第三项 ((1−cos⁡θ)/θ^2)ξ^2 修正非线性部分，确保生成的正交矩阵属于 SO(3)。

局部优化

我们可以利用指数映射的性质，通过指数映射转换为旋转增量，并与当前估计的旋转矩阵 R0组合：

$R_0\oplus\xi\triangleq R_0\cdot\exp\hat{\xi}$

接着，我们将非线性问题转换为局部坐标的线性最小二乘问题：

$\xi^*=\arg\min_\xi\|h(R_0\cdot\exp(\hat{\xi}))-z_a\|_\Sigma^2$

对其进行线性近似 $g^a(\xi;R_0)=h(R_0\cdot\exp(\hat{\xi}))$ 在 $\xi=0$ 处线性化：

$g^a(\xi;R_0)\approx h(R_0)+G_{R_0}^a\xi$

由此得到了线性优化的目标函数：

$\xi^*=\arg\min_\xi\|h(R_0)+G_{R_0}^a\xi-z_a\|_\Sigma^2$

求解方法

高斯-牛顿法：直接求伪逆解

$\xi^*=(G_{R_0}^a)^\dagger(z_a-h(R_0))$

由于测量函数h可能是高度非线性的，因此需要使用信赖域方法，如列文伯格-马夸尔特法：引入阻尼因子处理非线性强度，增强稳定性。

多传感器融合

加速度计只能测量重力方向，提供俯仰和滚转信息，但无法检测绕重力轴的旋转。这导致优化问题的雅可比矩阵 GR0a 秩不足，无法唯一确定三维旋转矩阵 R∈SO(3)。举个例子（若机器人绕垂直轴（重力方向）旋转，加速度计读数不变，优化算法无法感知这一旋转，导致解不唯一。）

此时，我们引入磁力计解决航向模糊性，磁力计测量地球磁场方向，提供绝对航向信息，可确定绕重力轴的旋转角。

融合方法：

将加速度计和磁力计的测量共同建模为因子图。

优化目标为最小化两者的联合残差：

$\xi^{*}=\underset{\xi}{\operatorname*{\mathrm{argmin}}}\|g^{a}(\xi;R_{0})-z_{a}\|_{\Sigma}^{2}+\|g^{m}(\xi;R_{0})-z_{m}\|_{\Sigma}^{2}$

$g^a$ 和 $g^m$ 分别是加速度计和磁力计的测量函数。
$z_a$ 和 $z_m$ 是实际测量值，Σ 为协方差矩阵。

平面旋转

直接使用角度 θ∈R表示平面旋转会遇到 2π 周期性环绕问题（例如 θ=2π 和 θ=0 等价），导致数值计算中的不连续。

为此引入SO2流形R（θ）（所有正交的2×2矩阵）表示旋转，自动处理周期性，避免了角度跳变。

$R(\theta)= \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}$

在这里我们定义李代数矩阵，对应平面旋转的生成元：

$\hat{\xi}= \begin{bmatrix} 0 & -\xi \\ \xi & 0 \end{bmatrix}$

将其进行指数映射：

$\exp(\hat{\xi})= \begin{bmatrix} \cos\xi & -\sin\xi \\ \sin\xi & \cos\xi \end{bmatrix}$

具体映射过程如下：

第一步：

矩阵指数的泰勒展开

$\exp(\hat{\xi})=\sum_{k=0}^\infty\frac{\hat{\xi}^k}{k!}$

对于反对称矩阵满足 $A^T=-A$ ，其幂次计算方法如下：

对于奇数次幂 $(A^n)^T=(A^T)^n=(-A)^n=(-1)^nA^n=-A^n$

对于偶数次幂，举个例子，设二维反对称矩阵 $A= \begin{pmatrix} 0 & a \\ -a & 0 \end{pmatrix}$

$A^2= \begin{pmatrix} 0 & a \\ -a & 0 \end{pmatrix} \begin{pmatrix} 0 & a \\ -a & 0 \end{pmatrix}= \begin{pmatrix} -a^2 & 0 \\ 0 & -a^2 \end{pmatrix}=-a^2I$

这是一个标量矩阵。对于更高次的偶数次幂，例如四次幂，这也是一个标量矩阵。

$A^4=(A^2)^2=(-a^2I)^2=a^4I$

幂次计算的规律如下：

第一阶： $\hat{\xi}^{1}=\begin{bmatrix}0&-\xi\\\xi&0\end{bmatrix}$

第二阶： $\hat{\xi}^{2}=-\xi^{2}I=\begin{bmatrix}-\xi^{2}&0\\0&-\xi^{2}\end{bmatrix}$

第三阶： $\hat{\xi}^{3}=-\xi^{2}\hat{\xi}$

第四阶： $\hat{\xi}^{4}=\xi^{4}I$

规律：奇数次幂保持反对称性，偶数次幂为标量矩阵。

第二步：

将奇数次项和偶数次项分别合并：

偶数次项： $I\left(1-\frac{\xi^2}{2!}+\frac{\xi^4}{4!}-\cdots\right)=\cos\xi\cdot I$

奇数次项： $\hat{\xi}\left(1-\frac{\xi^2}{3!}+\frac{\xi^4}{5!}-\cdots\right)=\frac{\sin\xi}{\xi}\cdot\hat{\xi}$

合并后得到： $\exp(\hat{\xi})=\cos\xi\cdot I+\frac{\sin\xi}{\xi}\cdot\hat{\xi}$

第三步：

将 $I= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ 和 $\hat{\xi}= \begin{bmatrix} 0 & -\xi \\ \xi & 0 \end{bmatrix}$ 代入得到：

$\exp(\hat{\xi})= \begin{bmatrix} \cos\xi & 0 \\ 0 & \cos\xi \end{bmatrix}+ \begin{bmatrix} 0 & -\sin\xi \\ \sin\xi & 0 \end{bmatrix}= \begin{bmatrix} \cos\xi & -\sin\xi \\ \sin\xi & \cos\xi \end{bmatrix}$

增量更新

定义完旋转矩阵后，我们可以按照以下规则进行更新：

初始旋转矩阵 $R_0=R(\theta_0)$ ，通过局部参数 $\xi$ 更新为

$R_0\oplus\xi=R_0\cdot\exp(\hat{\xi})= \begin{bmatrix} \cos(\theta_0+\xi) & -\sin(\theta_0+\xi) \\ \sin(\theta_0+\xi) & \cos(\theta_0+\xi) \end{bmatrix}$

PoseSLAM

在许多机器人应用中，我们更关心机器人随时间运动的轨迹，这里就引出了PoseSLAM。

PoseSLAM是同时定位与地图构建（SLAM）的一种变体，专注于优化机器人的位姿轨迹（位置与方向），而非显式构建环境地图。其核心目标是通过传感器数据（如激光雷达、里程计）重建机器人随时间变化的位姿序列。

在这里介绍一下传感器：

2D激光雷达

1、提供里程计约束：通过连续扫描生成相邻位姿间的相对运动估计。

2、提供闭环检测约束：当机器人重访已探索区域时，检测环境一致性以修正轨迹误差。

轮式里程计：提供初步的位姿变化估计。

位姿流形的表示和优化

核心思想是将非线性流形问题转换为线性空间中的无约束优化，同时严格保持几何约束。

位姿流形表示

平面位姿（SE(2)）

自由度：2D平移 (x,y)+ 航向角 θ，构成三维非线性流形。
数学形式：
$x\in SE(2)= \begin{bmatrix} \cos\theta & -\sin\theta & x \\ \sin\theta & \cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}$

三维位姿（SE(3)）

自由度：3D平移 (x,y,z)+ 3D旋转，构成六维非线性流形。
数学形式：

$x\in SE(3)= \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix},\quad R\in SO(3),\quad t\in\mathbb{R}^3$

位姿增量参数化

首先定义一下增量，由角速度 ω和平移速度 v 描述，结合时间步长 Δτ 生成增量：

$\xi\triangleq \begin{bmatrix} \omega \\ v \end{bmatrix}\Delta\tau$

Hat运算符：将增量转换为李代数元素，

SE(2)：

$\hat{\xi}= \begin{bmatrix} 0 & -\omega_z & v_x \\ \omega_z & 0 & v_y \\ 0 & 0 & 0 \end{bmatrix}\Delta\tau$

SE(3)：

$\hat{\xi}= \begin{bmatrix} 0 & -\omega_z & \omega_y & v_x \\ \omega_z & 0 & -\omega_x & v_y \\ -\omega_y & \omega_x & 0 & v_z \\ 0 & 0 & 0 & 0 \end{bmatrix}\Delta\tau$

指数映射

将李代数映射到李群上：

$x_{\mathrm{new}}=x_0\cdot\exp(\hat{\xi})$

SE(2)：

$\exp(\hat{\xi})= \begin{bmatrix} \cos\theta & -\sin\theta & v_x\Delta\tau \\ \sin\theta & \cos\theta & v_y\Delta\tau \\ 0 & 0 & 1 \end{bmatrix},\quad\theta=\omega_z\Delta\tau$

SE(3)：

$\exp(\hat{\xi})= \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix}$

其中旋转部分 R∈SO(3)，由罗德里格斯公式计算：

$R=I+\frac{\sin\theta}{\theta}\hat{\omega}+\frac{1-\cos\theta}{\theta^2}\hat{\omega}^2,$

$\theta=\|\omega\|$ 是旋转角度， $\hat{w}$ 是角速度的反对称矩阵。

平移部分 t∈R3，由位移积分公式计算：

$t=\left(I+\frac{1-\cos\theta}{\theta^2}\hat{\omega}+\frac{\theta-\sin\theta}{\theta^3}\hat{\omega}^2\right)v$

位姿优化

和之前类似，这里的目标是找到最优姿态x，使得测量残差的马氏范数最小化。

$x^*=\arg\min_x\|h(x)-z\|_\Sigma^2$

h是定义在流形上的非线性测量函数。

流形上的线性化

在基姿态x0附近展开：

$h(x_0\oplus\xi)\approx h(x_0)+H_0\xi$

其中H0是m*6的雅克比矩阵。

于是，原始非线性问题就被转换为：

$\xi^*=\arg\min_\xi\|h(x_0)+H_0\xi-z\|_\Sigma^2$

求解 $\xi^{*}$ 后，通过流形操作 $x_0\oplus\xi^*$ 更新姿态。

因子图

具体来说，PoseSLAM 因子图包含两种因子。

一元因子：包括先验姿态（如初始位置）或绝对测量（如 GPS 数据）f(x1)。

二元因子：主要来自里程计（Odometry）的相邻姿态间相对约束 f(xt,xt+1)。

在这里讲解一下书中给的例子：

红线 $f_5(x_5,x_2)$ 代表着循环闭合。

循环闭合：当机器人通过传感器识别到先前访问过的位置时，会生成跨时间姿态间的几何约束。

PoseSLAM 的最终目标是通过迭代优化所有位姿的局部坐标 $\Xi\triangleq\{\xi_i\}$ ，最小化残差和。

$\Xi^*=\underset{\Xi}{\operatorname*{\operatorname*{argmin}}}\left(\sum_i\|h(x_i)+H_i\xi_i-z\|_\Sigma^2+\sum_k\|g(x_i,x_j)+F_i\xi_i+G_j\xi_j-z\|_\Sigma^2\right),$

其中，一元项 h(xi)：对应单一位姿的测量（如 GPS）。

二元项 g(xi,xj)：对应相邻或跨时间姿态的测量（如里程计、循环闭合）。

雅可比矩阵 Hi,Fi,Gj：分别是一元/二元测量函数对局部坐标 $\xi_i$ ， $\xi_j$ 的导数，用于线性化非线性问题。

李群与一般流形上的优化方法

尽管旋转群SO（n）和刚体变换群SE（n）是机器人学中最常用的李群，但局部参数化技术可推广到任意矩阵李群和非群结构的非线性流形。有时忽略李群结构，采用非指数映射可能更高效，尤其在复杂流形优化中。

矩阵李群与李代数的基本工具

1、帽子算子

将向量空间 Rn 映射到李代数 g：

$\hat{\cdot}:\mathbb{R}^n\to\mathfrak{g},\quad\xi\mapsto\hat{\xi},$

2、vec算子：逆映射，将李代数元素还原为向量

$\vee:\mathfrak{g}\to\mathbb{R}^n,\quad\hat{\xi}\mapsto\xi$

3、指数映射

$a\oplus\xi\triangleq a\cdot\exp(\hat{\xi})$

非群结构流形上的优化方法

一般流形的收缩

对于任意流形 M，即使其不具备群结构，仍可通过定义 收缩映射 Ra: $\mathbb{R}^n\to\mathcal{M}$ ，将局部坐标 ξ∈Rn 映射回流形：

$a\oplus\xi\triangleq\mathcal{R}_a(\xi)$

关键性质：

平滑性：收缩映射需光滑（连续可导）。

恒等性：零坐标对应基点本身，即 Ra(0)=a。

球面 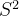$S^2$ 的收缩实现

球面定义为三维空间中单位向量的集合：

$S^2=\{p\in\mathbb{R}^3\mid\|p\|=1\}$

在点 p∈S^2 处，切平面定义为所有与 p 正交的向量构成的二维空间：

$T_pS^2\triangleq\{\tilde{\xi}\in\mathbb{R}^3\mid p^\top\tilde{\xi}=0\}$

基的选择方法

为什么要选择基呢？

建立局部坐标系：将二维优化变量与三维切平面无缝衔接。
简化流形操作：通过基的线性映射，将复杂的流形更新转化为欧氏空间中的优化问题。

基的构建：

1、构造单位矩阵Q=[Q1,Q2,Q3]，这里Q1=p。

2、选择一个任意向量v，不与p共线，这里可以通过施密特正交化使得这俩向量正交。

$Q_2=\frac{v-(p^\top v)p}{\|v-(p^\top v)p\|}$

3、接着，为了使得Q3与Q1,Q2都垂直，于是令Q3=Q1×Q2。

于是定义切平面基 Bp={Q2,Q3}。

局部坐标映射

局部坐标 ξ∈R2 通过基矩阵 Bp 映射到切平面向量 $\tilde{\xi}\in T_pS^2$

$\tilde{\xi}=B_p\xi=\xi_1Q_2+\xi_2Q_3$

此时， $\tilde{\xi}$ 自动满足 $p^\top\tilde{\xi}=0$ ，即位于切平面内。

收缩映射的实现

沿切平面方向移动：

$p+\tilde{\xi}=p+\xi_1Q_2+\xi_2Q_3$

归一化，确保新点 q 仍位于球面上：

$q=\mathcal{R}_p(\xi)=\frac{p+\tilde{\xi}}{\|p+\tilde{\xi}\|}$

李群与流形上的收缩方法

为确保几何一致性，要求在基点附近与指数映射导出的测地线一阶一致：

$\lim_{\xi\to0}\frac{\|a\cdot\exp(\hat{\xi})-\mathcal{R}_a(\xi)\|}{\|\xi\|}=0$

以刚体变换群 SE(3) 为例，提出一种计算更高效的收缩方式：

精确的指数映射会产生螺旋运动，需同时处理旋转与平移的耦合效应，计算复杂。

简化收缩方法将旋转与平移分离更新，公式为：

$\mathcal{R}_T(\xi)= \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} e^{\phi\Delta\tau} & v\Delta\tau \\ 0 & 1 \end{bmatrix}= \begin{bmatrix} Re^{\phi\Delta\tau} & t+Rv\Delta\tau \\ 0 & 1 \end{bmatrix}$