五、增量平滑与地图构建

tanshyu

已于 2025-04-30 11:31:50 修改

阅读量1.1k

点赞数 33

分类专栏： Factor Graphs 文章标签：人工智能图论机器人算法机器学习

于 2025-04-29 22:25:23 首次发布

本文链接：https://blog.csdn.net/qq_60073245/article/details/147457494

版权

Factor Graphs 专栏收录该内容

5 篇文章

订阅专栏

背景

传统批量优化算法假设所有数据预先可用，但实际机器人任务（如SLAM）中，数据是时序增量到达的，需要实时中间解。由于随着时间推移，优化问题规模指数增长，重复批量优化计算代价过高。所以，我们需要通过重用历史计算，避免全量更新，实现高效的增量优化。下面将分别从线性系统和非线性系统两方面展开。

线性系统的增量更新

又回到之前推倒过的线性化公式：

通过QR分解可以得到下式，这个已在前文推倒过，这里不重复介绍。

当检测到新的测量值时，我们这里不采用重新构造A’|b’的方法，避免全量更新。而是，通过扩展系统实现增量优化。设扩展系统:

对其进行QR分解：

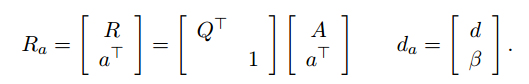
此时Ra尚未保持上三角形式，需通过Givens旋转消除新增行的非零元素。下面我们先介绍一下Givens旋转。

Givens旋转原理

HouseHolder是利用算子进行投影，一次将一个向量除第一个元素以外都转化成零。而有一种方法，可以每次将向量的一个元素转化成0，也可以最终达到正交化的目的，它就是Givens旋转。HouseHolder对于大量引进零元素是有用的，例如，消去一个向量中除第一个分量外的所有分量，然而，在许多计算中，必须有选择地消去一些元素。Givens旋转就是解决这些问题的工具。下面这个矩阵是单位矩阵的秩二矫正：

对于其中的某个 $\theta$ ， $c=cos(\theta ),s=sin(\theta )$ 显然Givens旋转是正交变换。

用 $G(i,k,\theta )^T$ 进行左乘产生一个在 $(i,k)$ 坐标平面的 $\theta$ 弧度的逆时针旋转。

其旋转后公式为：

在这里，我们令

使得 $y_k=0$ 。因此，使用Givens旋转很容易就可以将一个向量的某个分量的某个指定分量化为0。

Givens旋转的构造

Givens旋转矩阵形式为：

$G= \begin{bmatrix} \cos\phi & \sin\phi \\ -\sin\phi & \cos\phi \end{bmatrix}$

其作用是消除矩阵中特定位置的元素。对于新增行 $a^T$ ，从最左侧非零元素 $(i,j)$ 开始，选择旋转角度 $\phi$ 使得：

$\cos\phi=\frac{R_{j,j}}{\sqrt{R_{j,j}^2+a_j^2}},\quad\sin\phi=\frac{a_j}{\sqrt{R_{j,j}^2+a_j^2}}$

旋转后，目标位置 $(i,j)$ 的元素被归零。

于是，这里我们使用Givens变换的目的就很清楚了，就是将扩展矩阵Ra通过一系列Givens变换将对角线以下的元素全变为0，其数学表达式可以写为：

右侧向量da同步更新：

$d^{\prime}=G_{j_k}\cdots G_{j_2}G_{j_1}d_a$

基于此，我们可以写出通过增量变换后的目标函数：

其中 $c^{\prime}=c+\beta^2-\sum(d_i^{\prime})^2$ 为更新后的残差常数。

卡尔曼滤波与平滑

卡尔曼滤波器和平滑器是增量更新线性系统的特殊情况。为了与卡尔曼平滑器建立联系，我们首先描述因子图中边缘化的概念，然后讨论机器人技术中两种流行的基于边缘化的方法：固定滞后平滑和滤波。首先先介绍一下边缘化。

边缘化

即使使用增量更新，内存使用和计算在时间上仍然是无限的。一个解决方案是删除旧变量而不删除信息，这个过程称为边缘化。边缘化有三种处理方式，接下来将一一介绍。

1.若联合概率以协方差形式给出：

边缘化较为简单，协方差矩阵的块结构直接反映了边缘分布的协方差，直接取子块：

2.若联合概率以信息形式给出，边缘化后y的信息矩阵由Schur补给出。

具体应用中，选择协方差形式或信息形式取决于问题需求。信息形式更适合需要高效局部更新和稀疏性的场景，而协方差形式可能更直观用于直接概率解释。采用信息形式的主要原因是计算效率和算法设计的便利性，尤其在需要频繁边缘化、增量更新或处理稀疏结构的场景。

2.1 舒尔补

对于一个分块矩阵：

$M= \begin{bmatrix} A & B \\ C & D \end{bmatrix}$

假设子矩阵 A 可逆，则舒尔补定义为：

$S=D-CA^{-1}B$

由式子，我们可以直接理解为，用A将C消为0，D所在的位置保留着A的信息，将这个位置定义为S。

2.2 信息矩阵

将Σ分块为：

$\Sigma= \begin{bmatrix} \Sigma_{xx} & \Sigma_{xy} \\ \Sigma_{xy}^\top & \Sigma_{yy} \end{bmatrix}$

信息矩阵由其逆矩阵得到：

$\Lambda=\Sigma^{-1}= \begin{bmatrix} \Lambda_{xx} & \Lambda_{xy} \\ \Lambda_{xy}^\top & \Lambda_{yy} \end{bmatrix}$

信息矩阵可以看作对变量空间的“拉伸”或“压缩”操作。交叉项Λxy表示x和y的联合“拉伸方向”，边缘化需要调整剩余空间以消除x的拉伸影响。

2.3 分块信息矩阵与协方差矩阵的关系

边缘化变量x后，保留变量y的分布为：

其中μy是y的均值。在信息形式中，需表达为：

$p(y)=\mathcal{N}\left(\eta_y^{\prime},\Lambda_y^{\prime}\right)$

其中：

$\Lambda_y^{\prime}=\Lambda_{yy}-\Lambda_{xy}^{\top}\Lambda_{xx}^{-1}\Lambda_{xy}$

设联合高斯分布的信息形式为：

3.平方根信息矩阵的分解

若将信息矩阵分解为平方根形式 $\Lambda=R^\top R$ ，其中：

$R= \begin{bmatrix} R_{xx} & S_{xy} \\ 0 & R_{yy} \end{bmatrix}$

此时，边缘化后的信息矩阵为：

$\Lambda_y^{\prime}=\Lambda_{yy}-\Lambda_{xy}^\top\Lambda_{xx}^{-1}\Lambda_{xy}=R_{yy}^\top R_{yy}$

通过矩阵R的结构，边缘化可简化为直接截取 Ryy，避免显式计算Schur补，提升数值稳定性。

其联合概率可以表示为：

$p(x,y)=\mathcal{N}(R^{-1}d,R^{-1}R^{-\top})$

其中，

$R= \begin{bmatrix} R_{xx} & S_{xy} \\ 0 & R_{yy} \end{bmatrix}\quad d= \begin{bmatrix} d_{x} \\ d_{y} \end{bmatrix}$

以上三种形式的适用条件以表格的形式给出：

形式	边缘化难易度	数学操作	依赖条件	适用场景
协方差形式	容易	直接选择协方差矩阵	无	直接概率解释
信息形式	困难	Schur补计算	需要Schur补	需要增量更新，但未进行矩阵分解（如QR）
平方根信息形式	有条件容易	若变量是连续块且被优先消除，则直接移除矩阵的前nx行/列（保留 Ryy）	变量排序（需满足连续块消除条件）	增量优化、稀疏结构、数值稳定性