S&P2024 | 为何微小的鲁棒性会有帮助？进一步理解对抗迁移性

---

---

论文链接

本文 “Why Does Little Robustness Help? A Further Step Towards Understanding Adversarial Transferability” 聚焦对抗样本的可迁移性，从代理模型角度深入研究。通过定义模型平滑度和梯度相似性，剖析 “小鲁棒性” 现象，发现对抗训练中二者存在权衡关系，数据分布偏移会损害梯度相似性。研究数据增强和梯度正则化对可迁移性的影响，实验表明前者普遍降低可迁移性，后者能提升模型平滑度但与可迁移性的关系复杂。提出结合输入梯度正则化和锐度感知最小化（SAM）构建更好代理模型的通用方法，经实验验证该方法在提升可迁移性上效果显著，优于现有解决方案。

---

摘要-Abstract

Adversarial examples for deep neural networks (DNNs) are transferable: examples that successfully fool one white-box surrogate model can also deceive other black-box
models with different architectures. Although a bunch of empirical studies have provided guidance on generating highly transferable adversarial examples, many of these findings fail to be well explained and even lead to confusing or inconsistent advice for practical use.
In this paper, we take a further step towards understanding adversarial transferability, with a particular focus on surrogate aspects. Starting from the intriguing “little robustness” phenomenon, where models adversarially trained with mildly perturbed adversarial samples can serve as better surrogates for transfer attacks, we attribute it to a trade-off between two dominant factors: model smoothness and gradient similarity. Our research focuses on their joint effects on transferability, rather than demonstrating the separate relationships alone. Through a combination of theoretical and empirical analyses, we hypothesize that the data distribution shift induced by off-manifold samples in adversarial training is the reason that impairs gradient similarity.
Building on these insights, we further explore the impacts of prevalent data augmentation and gradient regularization on transferability and analyze how the trade-off manifests in various training methods, thus building a comprehensive blueprint for the regulation mechanisms behind transferability. Finally, we provide a general route for constructing superior surrogates to boost transferability, which optimizes both model smoothness and gradient similarity simultaneously, e.g., the combination of input gradient regularization and sharpness- aware minimization (SAM), validated by extensive experiments. In summary, we call for attention to the united impacts of these two factors for launching effective transfer attacks, rather than optimizing one while ignoring the other, and emphasize the crucial role of manipulating surrogate models.

深度神经网络（DNN）的对抗样本具有可迁移性：能够成功欺骗一个白盒代理模型的样本，也可以欺骗其他不同架构的黑盒模型。尽管大量实证研究为生成高可迁移性的对抗样本提供了指导，但其中许多发现难以得到充分解释，甚至在实际应用中给出了令人困惑或不一致的建议。
在本文中，我们朝着理解对抗样本可迁移性迈出了更进一步的步伐，特别聚焦于代理模型方面。从有趣的 “小鲁棒性” 现象出发，即用轻度扰动的对抗样本进行对抗训练的模型，可作为更好的代理模型用于迁移攻击。我们将这一现象归因于两个主要因素之间的权衡：模型平滑度和梯度相似性。我们的研究关注它们对可迁移性的联合影响，而不仅仅是单独探讨它们之间的关系。通过理论分析和实证研究相结合，我们假设对抗训练中流形外样本引起的数据分布偏移是损害梯度相似性的原因。
基于这些见解，我们进一步探究了常用的数据增强和梯度正则化对可迁移性的影响，并分析了这种权衡在各种训练方法中的表现形式，从而为可迁移性背后的调节机制构建了一个全面的蓝图。最后，我们提供了一种构建更优代理模型以提升可迁移性的通用方法，该方法可同时优化模型平滑度和梯度相似性，例如输入梯度正则化和锐度感知最小化（SAM）的组合，这在大量实验中得到了验证。总之，我们呼吁关注这两个因素的联合影响，以发起有效的迁移攻击，而不是优化一个因素而忽略另一个因素，并强调了操纵代理模型的关键作用。

---

引言-Introduction

该部分从研究背景与现状、本文研究目的和贡献展开论述，为后续研究内容的展开做了充分铺垫。

• 研究背景与现状
  • 对抗样本可迁移性：对抗样本具有可迁移性，即针对一个代理深度神经网络（DNN）生成的对抗样本，也能欺骗其他不同架构的 DNN。当前已提出多种提高对抗样本可迁移性的技术，如集成动量稳定更新方向、在每次迭代中应用变换创建多样输入模式等，但这些方法存在计算成本高、可扩展性低的问题。
  • 代理模型研究：部分研究开始关注代理模型在对抗样本可迁移性中的作用，如攻击不同架构的代理模型集成可获得更通用的对抗样本更新方向，以及微调预训练代理模型获取中间模型用于集成。然而，目前尚不清楚哪种代理模型性能最佳，以及如何构建更好的代理模型来实现更高的对抗可迁移性。
  • 相关理论解释：已有研究对对抗样本可迁移性的解释存在不足。Demontis 等人指出模型复杂性与梯度对齐分别与可迁移性呈负相关和正相关；Yang 等人建立了可迁移性下界，并将其与模型平滑度和梯度相似性联系起来，但对于这些因素仍有许多未知，如哪个因素对调节可迁移性更重要、现有提高可迁移性的经验发现如何影响这些因素，以及如何同时优化它们等。
• 研究目的与贡献
  • 研究目的：深化对对抗样本可迁移性的理解，并提供构建更好代理模型的具体指导，以增强对抗攻击效果。
  • 具体贡献
    • 理解“小鲁棒性”现象：深入探究“小鲁棒性”现象，将其归因于模型平滑度和梯度相似性之间的权衡，识别出对抗训练中梯度差异是由流形外样本导致的数据分布偏移造成的。
    • 研究数据增强影响：研究数据增强对可迁移性的影响，通过实验发现常用的数据增强方法会损害梯度相似性，且对模型平滑度的影响各异，最终导致可迁移性下降 。
    • 研究梯度正则化影响：探索梯度正则化对可迁移性的影响，实验表明梯度正则化普遍提高模型平滑度，但输入空间正则化在可迁移性方面不一定优于权重空间正则化，这与它们对梯度相似性的不同权重有关。
    • 提出构建代理模型的通用方法：提出一种构建具有优异平滑度和相似性代理模型的通用方法，即结合输入梯度正则化和锐度感知最小化（SAM），实验证明该方法能显著提升对抗样本的可迁移性，且可与独立于代理模型的方法集成，进一步提高可迁移性。

图1：本研究中调节对抗样本可迁移性的各因素之间关系的完整概述
表1：我们与该领域文献的关联概述

---

解释小鲁棒性-Explaining Little Robustness

符号-Notations

1. 空间与数据集符号：用 $X={\mathbb{R}}^d$ 表示输入空间，$y={\mathbb{R}}^m$ 表示输出空间。标准分类训练数据集记为 $S=\{(x_1,y_1),\cdots ,(x_n,y_n)\}$，其中 $x_i$ 来自正常（图像）特征流形 $M$ 且 $x_i\in M\subset X$，$y_i$ 取值于 $L=(0,1{)}^m\subset Y$，它们都独立同分布地从正常数据分布 $D\in P_{X\times Y}$ 中抽取。同时，$P_X$ 和 $P_y$ 分别表示 $x$ 和 $y$ 的边际分布。
2. 模型与函数符号：分类模型被看作是一个映射函数 $F:X\to L$，对于任意输入 $x\in X$，$F$ 通过 ${\ell }_F(x,y)$ 找到与硬标签 $c$ 的最优匹配，${\ell }_F(x,y)$ 可分解为训练损失 $\ell$ 和网络的 logits 输出 $f(\cdot )$，即 ${\ell }_F(x,y):=\ell (f(x),y)$. 本文中，代理模型和目标模型分别用 $F$ 和 $G$ 表示，且假设 $S$ 在 $D$ 上已训练良好，$D^{\prime }$ 表示与 $D$ 不同的数据分布 。

对抗训练的迁移性回路-Transferability Circuit of Adversarial Training

该部分聚焦对抗训练中的可迁移性变化规律，通过实验观察和理论分析相结合的方式，深入探讨了对抗训练中对抗样本可迁移性的 “transferability circuit” 现象，具体内容如下：

1. 对抗训练的损失函数：对抗训练（AT）通过将在训练集 $S$ 上生成的对抗样本作为增强数据，最小化对抗损失来训练模型。其对抗损失函数为 $L_{adv}=\frac{1}{\Vert S\Vert }{\sum }_{i=1}^{\Vert S\Vert }ma{x}_{\Vert \delta {\Vert }_2<ϵ}\ell \left(f\left(x_i+\delta \right),y_i\right)$，其中 $\delta$ 是对抗扰动，$ϵ$ 是对抗预算。
2. 可迁移性变化的实验观察：通过实验发现，对抗训练模型的攻击成功率（ASRs）呈现出随对抗预算变化的规律。在相对较小的对抗预算下训练的模型，攻击成功率会上升；而当对抗预算较高时，攻击成功率开始下降。这一现象被称为 “transferability circuit”，引起了研究人员的关注。
3. 基于理论工具的原因分析：为探究 “transferability circuit” 现象的内在原因，作者重新审视了先前提出的可迁移性下界理论，并将其作为分析工具。通过该理论，从模型平滑度、梯度相似性等因素出发，深入剖析对抗训练中各因素对可迁移性的影响，为后续进一步研究奠定了基础 。

图2：针对经过对抗训练的 CIFAR-10 和 ImageNette 分类器的迁移攻击成功率（ASR）。我们绘制了由3个随机种子得到的不同代理模型的平均结果，以及每个对抗预算值（$ϵ$）对应的误差条。

可迁移性下界-Lower Bound of Transferability

该部分主要围绕可迁移性下界展开，通过定义相关概念、给出可迁移性下界公式并分析各因素对其影响，深入探讨了影响对抗样本可迁移性的关键因素，具体内容如下：

1. 关键概念定义
   • 模型平滑度：给定模型 $F$ 和数据分布 $D$，模型平滑度 ${\sigma }_{F,D}={\mathbb{E}}_{(x,y)\sim D}[\sigma ({\nabla }_x^2{\ell }_F(x,y))]$，其中 $\sigma (\cdot )$ 表示主特征值，${\nabla }_x^2{\ell }_F(x,y)$ 是关于 $x$ 的 Hessian 矩阵。该定义从局部量化了模型损失曲面的平滑度，且与模型复杂度相关，为分析模型特性提供了量化指标。
   • 梯度相似性：对于两个模型 $F$ 和 $G$，其损失函数分别为 ${\ell }_F$ 和 ${\ell }_G$，梯度相似性 $S({\ell }_F,{\ell }_G,x,y)=\frac{{\nabla }_x{\ell }_F(x,y)\cdot {\nabla }_x{\ell }_G(x,y)}{{\Vert {\nabla }_x{\ell }_F(x,y)\Vert }_2\cdot {\Vert {\nabla }_x{\ell }_G(x,y)\Vert }_2}$. 基于此，还定义了在分布 $D$ 上损失梯度相似性的下确界 ${\underline{S}}_D({\ell }_F,{\ell }_G)$ 和期望损失梯度相似性 ${\tilde{S}}_D({\ell }_F,{\ell }_G)$，用于衡量两个模型在 $D$ 上的相似程度。
   • 可迁移性：给定正常样本 $(x,y)\in D$ 和针对代理模型 $F$ 生成的扰动版本 $x+\delta$，可迁移性 $T_r=\mathbb{I}[\mathcal{F}(x)=\mathcal{G}(x)=y\Lambda \mathcal{F}(x+\delta )\ne y\Lambda \mathcal{G}(x+\delta )\ne y]$，通过该定义明确了可迁移性的衡量标准，即代理和目标模型对未扰动输入预测正确，对扰动输入预测错误。
2. 可迁移性下界公式：给出可迁移性下界公式，对于给定样本 $(x,y)\in D$，设 $x+\delta$ 是 $x$ 的扰动版本，其愚弄代理模型 $F$ 的概率 $Pr(F(x+\delta )\ne y)\ge (1-\alpha )$ 且扰动预算 $\Vert \delta {\Vert }_2\le ϵ$，则代理模型 $F$ 和目标模型 $G$ 之间的可迁移性 $Pr(T_r(F,G,x,y)=1)$ 的下界为 $\frac{ϵ(1+\alpha )-c_F(1-\alpha )}{ϵ-c_G}-\frac{ϵ(1-\alpha )}{ϵ-c_G}\sqrt{2-2{\underline{S}}_D({\ell }_F,{\ell }_G)}$ $(\gamma F+\gamma G)$，其中涉及 $c_{\mathcal{F}}$、$c_{\mathcal{G}}$ 等参数，该公式为分析可迁移性提供了理论依据。
3. 各因素对可迁移性下界的影响
   • 愚弄概率：愚弄概率 $1-\alpha$ 反映了代理模型 $F$ 被对抗样本 $x+\delta$ 愚弄的可能性，不同的对抗样本生成策略会导致不同的愚弄概率，较大的愚弄概率有利于提高可迁移性下界，因此默认使用强基线攻击方法。
   • 自然风险：模型在数据分布 $D$ 上的自然风险 ${\gamma }_F$ 对可迁移性下界有负面影响，低准确率的模型不利于对抗攻击，所以通过充分训练模型来最小化该风险。
   • 梯度相似性：梯度相似性 ${\underline{S}}_D({\ell }_F,{\ell }_G)$ 与可迁移性下界呈正相关，较大的梯度相似性对应更大的可迁移性下界。
   • 模型平滑度：较小的模型平滑度 ${\bar{\sigma }}_F$ 会使 $c_F$ 更大，从而产生更大的可迁移性下界，意味着更平滑的模型可能更适合作为迁移攻击的代理模型。

对抗训练下的权衡-Trade-off Under Adversarial Training

这部分内容主要研究对抗训练中模型平滑度和梯度相似性之间的权衡关系，以及这种权衡对对抗样本可迁移性的影响，具体内容如下：

1. 权衡关系的提出：通过理论分析和实验测量，研究发现从代理模型的角度来看，模型平滑度和梯度相似性之间的权衡对对抗样本的可迁移性有显著影响。对抗训练（AT）在提升模型平滑度的同时，会损害梯度相似性。
2. AT对模型平滑度的影响：从理论上，通过重写对抗损失函数并进行泰勒展开，发现AT会隐式地惩罚损失函数 $\ell (f(x_i),y_i)$ 的曲率，且惩罚程度与对抗噪声的范数 $\Vert \delta {\Vert }_2^2$ 成正比。因此，较大的对抗预算 $ϵ$ 能强化产生更平滑模型的效果。实验结果也表明，AT 能持续抑制 Hessian 矩阵的主特征值，稳定地产生更平滑的模型。
3. AT对梯度相似性的影响：通过实验发现，随着对抗预算 $ϵ$ 的增加，代理模型和目标模型之间的梯度相似性会逐渐下降。例如，在不同数据集上的实验显示，当 $ϵ$ 增大时，梯度相似性呈衰减趋势。
4. 权衡对可迁移性的影响：在对抗训练中，当 $ϵ$ 较小时，模型平滑度快速提升，同时梯度相似性下降较小，此时对抗样本的可迁移性快速提高；当 $ϵ$ 较大时，模型平滑度的提升逐渐达到极限，而梯度相似性持续下降，导致对抗样本的可迁移性降低。这表明对抗训练中可迁移性的变化主要源于模型平滑度和梯度相似性之间的权衡。
5. 数据分布偏移的影响：研究认为对抗训练中梯度相似性的恶化是由数据分布偏移引起的。由于对抗样本可能位于数据流形之外，随着对抗预算 $ϵ$ 的增加，数据分布偏移增大，更多的流形外样本出现，进而损害了梯度相似性。基于此提出假设：分布偏移会损害梯度相似性，即当两个数据分布之间的距离足够大时，在不同分布上训练的模型之间的梯度相似性可能会降低。

图3：在3个不同随机种子下训练的具有 $ϵ$ 鲁棒性的模型的平均模型平滑度，每个 $ϵ$ 值都带有相应的误差条。请注意，方差非常小。

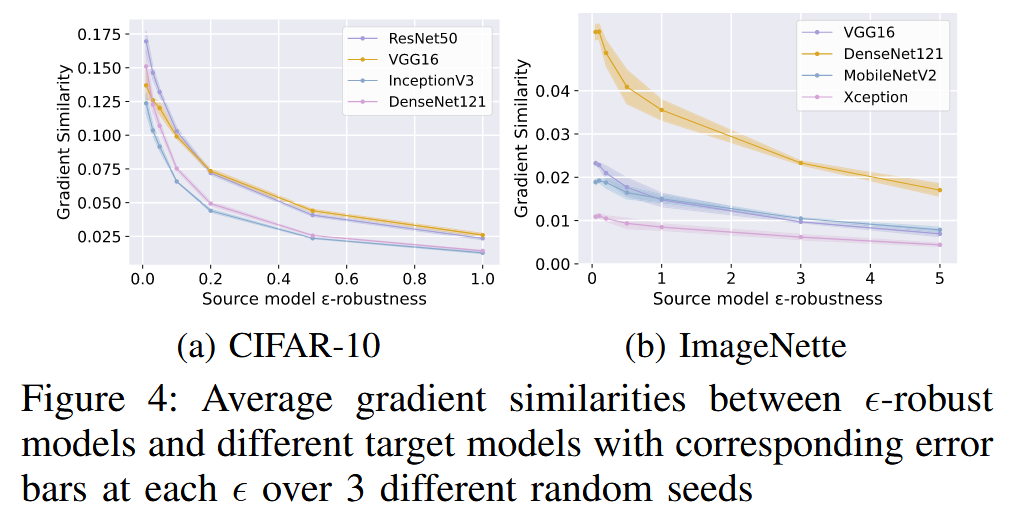
图4：在3个不同随机种子模型以及不同目标模型下，$ϵ$ 鲁棒模型之间的平均梯度相似性。

---

数据增强探究-Investigating Data Augmentation

数据增强机制-Data Augmentation Mechanisms

该部分主要介绍了研究中探索的 4 种数据增强机制，包括 Mixup、Cutmix、Cutout 和 Label smoothing，以及它们的具体操作方式和用于控制数据分布变化程度的参数设置，具体内容如下：

1. Mixup（MU）：Mixup 通过对随机选择的样本对进行凸组合来训练模型。混合图像 ${\tilde{x}}_{i,j}=b{x}_i+(1-b)x_j$，相应标签 ${\tilde{y}}_{i,j}=b{y}_i+(1-b)y_j$，其中 $(x_i,y_i)$，$(x_j,y_j)\in S$，$b\in [0,1]$ 是从 Beta(1, 1) 分布中随机抽取的变量。通过概率参数 $p$ 控制数据分布从 $D$ 到 $D^{\prime }$ 的偏移程度，$p\to 0$ 时，增强数据集与 $S$ 相同；$p\to 1$ 时，所有样本都将被插值。实验中训练增强模型的 $p\in [0.1,0.3,0.5,0.7,0.9]$.
2. Cutmix（CM）：Cutmix 同样对图像和标签进行混合增强，与 Mixup 的区别在于它是在训练样本之间进行 patch 的切割和粘贴。混合样本 ${\tilde{x}}_{i,j}=M_b\odot x_i+(1-M_b)\odot x_j$ 及其标签 ${\bar{y}}_{i,j}$ 由两个样本 $(x_i,y_i)$，$(x_j,y_j)\in S$ 得到，其中 $M_b$ 是与 $x_i$ 大小相同的二进制矩阵，用于指示切割和粘贴的位置，$b$ 从 Beta(1, 1) 分布中抽取。和 Mixup 一样，使用概率参数 $p$ 控制增强幅度，实验中 $p\in [0.1,0.3,0.5,0.7,0.9]$.
3. Cutout（CO）：Cutout 通过在图像上随机遮挡小于 $M\times M$ 的区域来增强数据集。在实际操作中，每个图像的遮挡区域和大小是不确定的，更大的 $M$ 值表示更有可能遮挡更大的区域。因此利用 $M$ 的值来调节增强程度，类似于 Mixup 和 Cutmix 中 $p$ 的作用。对于 CIFAR-10 和 ImageNette 数据集，分别选择 $M\in [8,12,16,20,24]$ 和 $M\in [80,100,120,140,160]$.
4. Label smoothing（LS）：Label smoothing 通过用软连续标签替换硬标签来增强数据集。真实类别的概率为 $1-p$，其他类别的概率将均匀分配为 $p/(m-1)$，其中 $p$ 从 $[0,1)$ 中选择，$m$ 表示类别数。实验中训练模型的 $p\in [0.1,0.2,0.3,0.4,0.5]$.

这些数据增强方法与对抗训练（AT）以不同方式改变数据分布，对梯度 $\nabla {\ell }_F(x,y)$ 产生不同影响。为简化表示，使用通用参数 $\tau \in [1,2,3,4,5]$，例如 $\tau =1$ 对于 $MU$ 意味着 $p=0.1$，对于 $CO$ 在 CIFAR-10 中意味着 $M=8$.

数据增强损害相似性-Data Augmentation Impairs Similarity

该部分主要研究数据增强对梯度相似性的影响，旨在验证 “数据分布偏移会损害梯度相似性” 这一假设，具体内容如下：

1. 实验设置：为探究不同数据分布变化对梯度相似性的影响，针对4种数据增强机制（Mixup、Cutmix、Cutout和Label smoothing）进行实验。在每个设置中，使用3个不同的随机种子训练模型，并考虑多个目标模型以确保实验结果的通用性。将3个标准训练（ST）模型（无增强）的结果作为基线。
2. 实验结果分析
   • Cutout的影响：Cutout 对梯度相似性的损害最小，但在不同数据集上表现不同。在 CIFAR-10 中，它轻微降低梯度相似性；在 ImageNette 中，其效果与基线相当。这可能是因为 CIFAR-10 模型是从头开始训练，而 ImageNette 模型是通过微调预训练的 ImageNet 分类器得到，简单去除一些像素不足以让 ImageNette 模型忘记之前“看到”的信息。
   • Label smoothing、Mixup 和 Cutmix 的影响：Label smoothing、Mixup 和 Cutmix 在两个数据集上都大幅降低了梯度相似性。这些增强方法对相似性的降低程度与它们对 $P_y$ 的操作一致，表明在训练过程中修改真实标签 $y$ 会对梯度 $\nabla {\ell }_F(x,y)$ 的方向产生更大影响。
3. 结论：尽管不同数据增强方法对梯度相似性的影响存在细微差异，但两个数据集上的实验结果都支持“数据分布偏移会损害梯度相似性”这一假设。此外，研究还发现 $P_y$ 中的分布变化对相似性的负面影响可能比 $P_X$ 中的更大。

图5：增强后的代理模型与标准训练（ST）的目标CIFAR-10模型之间的梯度相似性，每个T值都带有误差条。

图6：增强后的代理模型与标准训练（ST）的目标ImageNette模型之间的梯度相似性，每个T值都有误差条。

数据增强下的权衡-Trade-off Under Data Augmentation

该部分主要研究了数据增强下模型平滑度、梯度相似性与对抗样本可迁移性之间的权衡关系，具体内容如下：

1. 实验目的：探究不同数据增强方法对模型平滑度和对抗样本攻击成功率（ASRs，衡量可迁移性的指标）的影响，分析在数据增强情况下，模型平滑度和梯度相似性之间的权衡如何反映在对抗攻击中。
2. 实验方法：测量不同数据增强模型的平滑度和对抗样本的ASRs，为节省空间，主要报告了PGD攻击下 $\tau =1,5$（分别代表最小和最大增强幅度）的情况，以及 AutoAttack 下 $\tau =1,3,5$ 的情况，并绘制了增强模型在两个数据集上的平滑度图表。
3. 实验结果与分析
   • Label smoothing（LS）的影响：LS 在两个数据集上对模型平滑度都有单调的提升作用，这是因为它在训练过程中能隐式地降低梯度范数。然而，其对抗样本的 ASRs 始终低于标准训练（ST）模型，这意味着 LS 对平滑度的提升并不能完全抵消其对梯度相似性的负面影响。此外，LS 的 ASRs 没有单调性，体现了其正负效应的相互对抗。
   • 其他增强方法的影响：Mixup（MU）、Cutmix（CM）和Cutout（CO）在两个数据集上对平滑度的影响并不一致。在 CIFAR-10 中，它们大多降低了平滑度，且这种降低并非严格单调；在 ImageNette 中，平滑度的变化更加混乱，方差较大。从 ASRs 来看， CM 和 MU 的 ASRs 随着增强幅度从 $\tau =1$ 增加到 $\tau =5$ 而下降，CO 的 ASRs 总体上比 MU 和 CM 更好，在某些情况下甚至略优于 ST 模型，这与其相对较好的平滑度和较小的梯度相似性下降程度相符。
4. 结论：数据增强下的权衡关系较为复杂，没有一种数据增强方法能单独产生良好的代理模型用于对抗攻击。不同的数据增强方法对模型平滑度和梯度相似性有不同的影响，进而影响对抗样本的可迁移性，在实际应用中需要综合考虑这些因素 。

表2：在CIFAR-10数据集上，针对基线模型（$(ST)$）、数据增强方法、对抗训练以及梯度正则化代理模型，在不同的 $L_{\infty }$ 预算（4/255、8/255、16/255）下，由投影梯度下降法（PGD）生成的对抗样本（AE）的无目标和有目标迁移攻击成功率（ASR）。灰色结果表示比基线低（超过0.2%），白色结果表示与基线接近（±0.2%）。最深橙色结果表示各列中最高值，次深橙色表示第二高值，颜色最浅的表示比基线高超过0.2%的其他结果。我们在每种设置下使用从3个不同随机种子训练的代理模型进行实验，并报告平均结果（以百分比表示）和相应的误差条。

表3：使用投影梯度下降法（PGD）在ImageNette数据集上，对抗样本（AE）的迁移攻击成功率（以百分比表示）。我们以与表2相同的方式绘制此表。

图7：CIFAR-10数据集上增强模型的平均模型平滑度，每个 $T$ 值对应的误差条也一并展示 。

图8：ImageNette数据集上增强模型的平均模型平滑度，每个 $T$ 值对应的误差条也一并展示。

---

梯度正则化研究-Investigating Gradient Regularization

梯度正则化机制-Gradient Regularization Mechanisms

该部分主要介绍了梯度正则化的相关机制，包括输入空间和权重空间的梯度正则化方法，具体内容如下：

1. 输入空间的梯度正则化
   • 输入梯度正则化（IR）：基于正则化输入空间平滑度有利于提高对抗样本可迁移性的理论，IR 直接将输入的梯度的欧几里得范数添加到损失函数中，公式为 $L_{ir}=\frac{1}{\Vert S\Vert }{\sum }_{i=1}^{\Vert S\Vert }\left[\ell \left(f\left(x_i\right)\right)+{\lambda }_{ir}\Vert {\nabla }_x\ell \left(f\left(x_i\right)\right)\Vert \right]$，其中 ${\lambda }_{ir}$ 控制正则化强度。由于矩阵的谱范数上限由 Frobenius 范数界定，通过正则化 ${\Vert {\nabla }_x\ell (f(x))\Vert }_2$ 可使 $\sigma ({\nabla }_x^2\ell (x))$ 更小，从而提高模型平滑度，进而提升对抗样本可迁移性。
   • 输入雅可比正则化（JR）：JR 对网络 logits 输出的梯度进行正则化，公式为 $L_{jr}=\frac{1}{\Vert S\Vert }{\sum }_{i=1}^{\Vert S\Vert }\left[\ell \left(f_{\theta }\left(x_i\right)+{\lambda }_{jr}{\Vert {\nabla }_x{f}_{\theta }\left(x_i\right)\Vert }_F\right]\right)$. 以交叉熵损失为例证明了，当 ${\Vert {\nabla }_x{f}_{\theta }(x_i)\Vert }_F\to 0$ 时，$\Vert {\nabla }_x\ell (f_{\theta }(x_i))\Vert \to 0$，这表明 JR 对模型平滑度有积极影响。
2. 权重空间的梯度正则化
   • 显式梯度正则化（ER）：ER 将关于权重 $\theta$ 的梯度的欧几里得范数添加到训练损失中以促进平坦性，公式为 $L_{er}(\theta )=L(\theta )+\frac{{\lambda }_{er}}{2}{\Vert {\nabla }_{\theta }L(\theta )\Vert }^2$，其中 $L$ 是原始目标函数，${\lambda }_{er}$ 控制正则化强度。已有研究从泛化角度对其进行了探讨，本文从可迁移性角度进行研究。
   • 锐度感知最小化（SAM）：SAM 旨在权重空间中寻找平坦解，通过最小化原始训练损失和最坏情况锐度来实现，公式为 $L_{sam}(\theta )=L(\theta )+[ma{x}_{\Vert \hat{\theta }-\theta {\Vert }_2\le \rho }L(\hat{\theta })-L(\theta )]=ma{x}_{\Vert \hat{\theta }-\theta {\Vert }_2\le \rho }L(\hat{\theta })$，其中 $\rho$ 是搜索最坏邻居 $\hat{\theta }$ 的半径。由于精确的最坏邻居难以追踪，SAM 通过两次近似使用梯度上升方向邻居进行更新。近期研究将 SAM 视为一种特殊的梯度归一化，本文首次证实 SAM 在提升对抗样本可迁移性方面具有显著优势。

梯度正则化促进平滑性-Gradient Regularization Promotes Smoothness

这部分内容主要研究了梯度正则化对模型平滑度的影响，通过实验对比不同梯度正则化方法，得出相关结论，具体如下：

1. 实验设置：为探究梯度正则化对模型平滑度的影响，针对每种梯度正则化方法（IR、JR、ER 和 SAM）训练多个正则化模型。采用粗粒度参数区间，并限制最大正则化强度，确保模型准确率在 90% 以上，以在可接受的准确率范围内公平比较各正则化方法。在每个区间通过随机梯度和二元选择选取5个参数。
2. 实验结果：通过对 CIFAR-10 和 ImageNette 数据集上的实验结果（如模型平滑度图表）分析可知，梯度正则化通常能使模型比未进行正则化的基线模型（ST）更平滑，即具有更小的模型平滑度值，且较大的正则化强度对应更好的平滑度。此外，输入梯度正则化方法（IR 和 JR）在提升模型平滑度方面表现更优且更稳定，其方差较小，尤其在 CIFAR-10 数据集上更为明显。这表明虽然权重空间到输入空间的梯度正则化迁移效应存在，但相对较弱，无法超越直接在输入空间进行的正则化方法。

图9：CIFAR-10数据集上正则化模型的模型平滑度，每个 $\tau$ 值都有相应的误差条。这些模型的标准准确率在90.12%到95.38%之间。

图10：ImageNette数据集上正则化模型的模型平滑度，每个 $\tau$ 值都有相应的误差条。这些模型的标准准确率在90.62%到96.91%之间。

梯度正则化下的权衡-Trade-off Under Gradient Regularization

该部分主要探讨梯度正则化下模型平滑度与可迁移性之间的权衡关系，通过实验分析发现两者关系并非简单的正相关或负相关，具体内容如下：

1. 预期与实际结果的差异：按照 Demontis 等人的结论，模型复杂度与可迁移性相关，且平滑度与模型复杂度正相关，那么输入梯度正则化（JR、IR）在提升平滑度的同时，应在可迁移性方面优于权重梯度正则化（SAM、ER）。
2. 实验结果分析：在 CIFAR-10 数据集上，针对不同目标模型和对抗预算，进行无目标和有目标攻击实验。结果显示，SAM 在无目标攻击的12个案例中有11个、有目标攻击的12个案例中全部，表现优于 IR；在无目标攻击的12个案例中有11个、有目标攻击的12个案例中有7个，表现优于 JR。而在ImageNette数据集上，情况则相反，SAM 在无目标攻击的12个案例中有11个、有目标攻击的12个案例中有10个，表现不如 IR；在无目标和有目标攻击的所有12个案例中，都不如 JR。
3. 结论：这些不一致的实验结果表明，不能简单认为更好的平滑度就一定会带来更好或更差的可迁移性。这一发现不仅削弱了Demontis等人的结论，还提示在构建更优代理模型时，需要全面综合地考虑各种训练机制对模型平滑度和梯度相似性的不同影响，因为它们在不同数据集上对可迁移性的影响存在差异 。

---

提升代理模型的可迁移性-Boosting Transferability from Surrogates

构建更优代理模型的通用方法-A General Route for Better Surrogates

该部分主要提出了一种构建更优代理模型以提升对抗样本可迁移性的通用方法，通过分析不同训练机制的优缺点，发现SAM与输入正则化具有互补性，将二者结合可有效提升可迁移性，具体内容如下：

1. 梯度正则化机制的观察
   • 输入正则化对平滑度的影响：输入正则化方法（IR 和 JR）在提升模型平滑度方面表现出色，从模型平滑度实验结果可知，它们能稳定地产生较高的平滑度，且方差较小。相比之下，其他如 SAM、ER 等有助于平滑度提升的机制在这方面表现较弱。此外，IR、JR 和对抗训练（AT）在输入空间上都有直接的惩罚作用，使得它们之间的梯度对齐效果较好。
   • SAM对梯度相似性的影响：当不涉及输入正则化时，SAM 在梯度对齐方面表现最佳。通过测量不同机制下代理模型之间的梯度相似性发现，SAM 对各种机制的梯度对齐效果均优于标准训练（ST）。在排除对角线元素后，SAM 在大部分情况下，其梯度相似性在各行列中表现突出，仅在与 IR、JR 和 AT 比较时优势不明显，这表明 SAM 在提升梯度相似性方面具有独特优势。
     
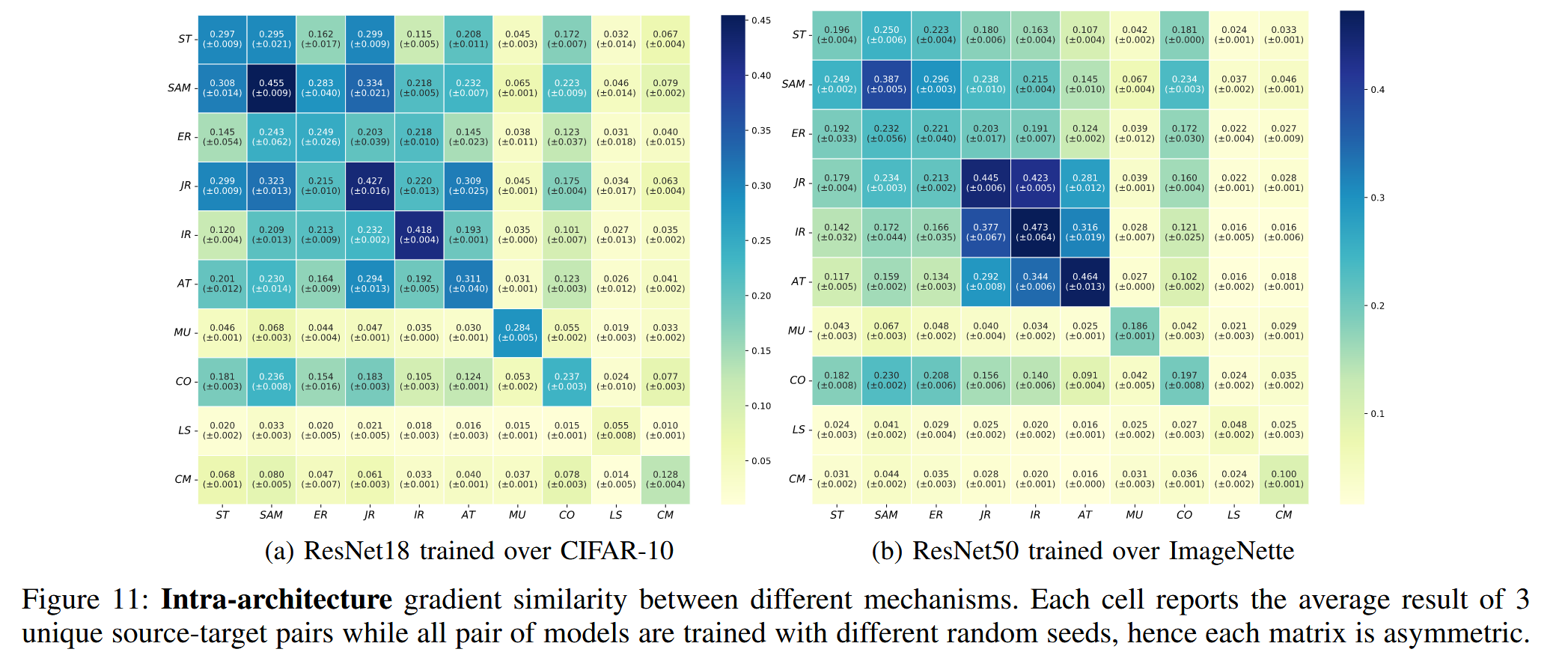
     图11：不同机制之间的架构内梯度相似性。每个单元格展示了3组独特的源-目标模型对的平均结果，并且所有的模型对都是用不同的随机种子训练的，因此每个矩阵都是非对称的。
   • 不同机制在数据集上的表现差异：不同的训练机制在不同数据集上的表现各有优劣。在 CIFAR-10 数据集上，SAM 平均能取得最佳的攻击成功率（ASRs），但在 ImageNette 数据集上，它的表现通常不如 IR 和 JR。而 ER 在两个数据集上的表现都相对较差，没有一种机制能在所有数据集上都显著优于其他机制。
2. 构建更优代理模型的方法：基于上述观察，发现 SAM 和输入正则化具有很强的互补性。为在模型平滑度和梯度相似性之间达到更好的权衡，提出将 SAM 与输入正则化相结合的方法，即 SAM&IR 或 SAM&JR。通过在 CIFAR-10 和 ImageNette 数据集上进行实验验证，结果表明 SAM&JR 和 SAM&IR 在提升对抗样本可迁移性方面表现最佳，显著优于其他方法。不过，文章也指出构建更好代理模型的方法不限于这两种组合，只要能合理协调模型平滑度和梯度相似性之间的权衡，其他组合或方法也可能有效。

结合代理模型无关的方法-Incorporating Surrogate-independent Methods

该部分主要阐述了如何将代理模型相关方法与独立于代理模型的方法相结合，进一步提升对抗样本的可迁移性，具体内容如下：

1. 结合 AE 生成策略：利用对抗样本（AE）生成过程是提升可迁移性的常用方法，如动量迭代（MI）和多样性迭代（DI），两者结合的多样性迭代与动量（DIM）是更强的基线方法。通过实验验证，使用更优的代理模型（如具有较少且更宽泛局部最优解和通用对抗方向的模型）能够进一步增强这些设计的效果。实验结果表明，在不同的生成策略（PGD、MI 和 DIM）下，使用更好的代理模型（如 SAM 和 SAM&JR）总能显著提升对抗样本的可迁移性。甚至在没有 MI 或 DIM 的情况下，SAM&JR 仅使用标准 PGD 就超过了 ST+MI 和 ST+DMI 的效果，说明更好的代理模型具有更高的可迁移性下限。
   表4：在CIFAR-10数据集上，在不同的 $L_{\infty }$ 预算下结合对抗样本（AE）生成策略时的无目标和有目标迁移攻击成功率（以百分比表示）。由于随机化情况不同，相应结果与表2中的结果有所不同。
   

2. 结合集成策略：使用多个代理模型的集成策略被认为可以使对抗样本更新方向更通用，从而提升可迁移性。近期研究提出从大几何邻域（LGV）构建集成模型，即先微调正常训练的模型得到一组中间模型，再针对这些模型迭代优化对抗样本。通过在 CIFAR-10 上的实验验证，发现使用 SAM 和 SAM&JR 进行微调得到的模型，其 LGV 集成在攻击成功率（ASR）上优于标准 SGD 微调的模型，表明 SAM 和 JR 的内在特性有助于找到对可迁移性有益的解。然而，用 SGD 对 SAM 和 SAM&JR 得到的模型进行微调会对可迁移性产生负面影响，这意味着 SAM 和 SAM&JR 训练得到的模型处于对可迁移性更有利的吸引盆中，而 SGD 的高学习率微调可能会使模型离开这个吸引盆。由此推断，大邻域可能不是可迁移性的决定因素，与可迁移性内在相关的密集子空间更值得关注。
   表5：在CIFAR-10数据集上，在不同的 $L_{\infty }$ 预算下，针对单个代理模型和大几何邻域（LGV）集成代理模型生成的对抗样本（AE）的无目标和有目标迁移攻击成功率（以百分比表示）。基线使用未经微调的初始代理模型，并与LGV集成模型进行比较。在每次比较中，我们将最佳的攻击成功率以粗体突出显示，将低于基线的结果以红色标出。
   

3. 结合其他策略的展望：AE 生成和集成策略是目前研究较多的方法，而其他因素如损失对象修改、架构选择、$l_2$-范数考虑、无限制生成、基于 patch 的对抗样本等也可能对可迁移性有贡献。将这些因素与当前设计相结合的研究留待未来工作进行探索。

---

分析与讨论-Analyses and Discussions

该部分对研究过程中的多个关键问题进行了深入分析和讨论，旨在进一步阐释研究成果，揭示各因素之间的潜在关系，为理解对抗样本可迁移性提供更多视角，具体内容如下：

1. 平滑度与相似性对可迁移性的影响：通过计算 Pearson 相关系数和进行普通最小二乘法（OLS）回归分析，研究发现模型平滑度和梯度相似性都与攻击成功率（ASR）高度相关，且二者的联合效应显著。随着对抗预算 $ϵ$ 增加，平滑度与 ASR 的相关性增强，相似性与 ASR 的相关性减弱，这表明在不同 $ϵ$ 下，应采用自适应的相似性 - 平滑度权衡策略来构建代理模型。
   表6：攻击成功率（ASR）与准确率（Acc）、误判概率（FP）、模型平滑度（MS）以及梯度相似性（GS）之间的皮尔逊相关系数（(r)）。对于普通最小二乘法（OLS）中的决定系数（$R^2$），$R_1^2$ 表示模型平滑度（MS）和梯度相似性（GS）对攻击成功率（ASR）的联合影响，(R_{2}^{2})表示这四个因素的联合影响。
   

2. 目标模型训练分布的影响：放松目标模型训练数据分布的限制后，提出假设：在正常数据分布 $D$ 上训练的代理模型，比在其他分布 $D^{\prime }$ 上训练的代理模型，能更好地与一般目标模型对齐。通过实验，对比不同代理模型与目标模型之间的梯度相似性和迁移ASR，验证了该假设。结果表明，除了小预算对抗训练的代理模型外，在 $D^{\prime }$ 上训练的代理模型通常会恶化梯度对齐，而在 $D$ 上训练的代理模型大多能改善对齐。在迁移 ASR 方面，无论目标模型的训练分布如何，SAM&IR 或 SAM&JR 通常都是最佳代理模型。
   表7：CIFAR-10数据集上代理模型-目标模型对（残差网络18-视觉几何组16）之间的跨架构梯度相似性。第一行报告标准训练（$ST$）代理模型的结果，其下方报告与标准训练（$ST$）的差异。最后一列根据对多个目标的总体一致性对代理模型进行评分。（正值累加 +1，负值累加 -1。）
   
   表8：在CIFAR-10数据集上，由各种残差网络18（ResNet18）代理模型生成的对抗样本（AE）针对经过对抗训练（AT）和数据增强处理的视觉几何组16（VGG16）目标模型的迁移攻击成功率。“⋆”表示代理模型的训练方法与相应目标模型的训练方法相同。“T”代表“有目标”攻击，“U”代表“无目标”攻击。
   

3. 模型平滑度与复杂度的关系：模型复杂度与可迁移性相关，而模型平滑度与模型复杂度呈负相关。因为高复杂度模型的多个局部最优会导致对抗样本优化的损失景观方差较大，而促进模型平滑度可使有限 $ϵ$-邻域内的最优解更少且更宽泛，所以更平滑的模型意味着更低的复杂度。

4. 模型泛化与可迁移性的关系：有研究试图表明模型泛化与对抗样本可迁移性之间存在正相关，但本文指出这种关系不能一概而论。通过实验发现，一些能提升模型泛化能力的数据增强方法，如 Mixup 和 Cutmix，实际上会损害可迁移性。这是因为它们在提升泛化时，可能通过破坏相似性等方式降低了可迁移性。

5. ViT对抗可迁移性的限制因素：针对 ViT 对抗可迁移性较低的问题，一种观点认为是当前攻击方法不够强，而本文提出 ViT 的训练范式可能是限制其可迁移性的原因。ViT 通常需要大规模预训练和强数据增强，而这些操作可能改变数据分布，损害梯度相似性。实验表明，使用不同训练方法（如SAM）训练的 ViT，其可迁移性显著提高，证明了训练范式对 ViT 可迁移性的影响。
   表9：针对基于视觉Transformer（ViT）的ImageNet代理模型生成的对抗样本（AE）对目标模型的无目标迁移攻击成功率（以百分比表示）
   

6. 实验结论的现实适用性：针对 “实验室” 结论在现实环境中可能不成立的观点，通过在三个商业机器学习即服务（MLaaS）平台（AWS Rekognition、阿里巴巴云、百度云）上进行实验，验证了本文结论的通用性。实验结果与 “实验室” 结果基本一致，且与之前研究中“对抗训练和数据增强与迁移攻击没有强相关性”的观点相悖，表明强数据增强通常会降低 ASR，而“小鲁棒性”可提升可迁移性，大对抗幅度则会降低可迁移性。
   表10：使用表3中所报告的对抗样本（AE），在3个机器学习即服务（MLaaS）平台上，处于不同 $L_{\infty }$ 预算下的迁移攻击成功率（以百分比表示）
   

7. SAM性能优势的原因探讨：SAM 在提升可迁移性和梯度对齐方面表现优异，一种推测是其优化的单个模型代表了多个模型的集成（期望），攻击 SAM 训练的模型类似于攻击多个模型的集成，从而提升了可迁移性。但目前这只是直观推测，SAM 的泛化优势等特性仍有待进一步研究。

---

相关工作-Related Work

该部分主要围绕对抗样本的可迁移性，梳理了当前的研究成果，阐述了本文与已有研究的关联与区别，具体内容如下：

1. 对抗样本可迁移性的生成技术：过去研究提出多种生成高可迁移性对抗样本的方法。包括基于优化的方法，如在每次迭代中应用变换以创建多样输入模式、集成动量稳定更新方向等；基于数据增强的方法，像使用无限制对抗样本、添加噪声等。这些方法旨在生成能有效欺骗不同模型的对抗样本，但存在计算成本高、可扩展性低等问题。
2. 对抗样本可迁移性的理论解释：部分研究从理论层面探讨对抗样本可迁移性的原因。Demontis等人发现模型复杂性与梯度对齐分别与可迁移性呈负相关和正相关；Yang等人建立可迁移性下界，将其与模型平滑度和梯度相似性联系起来。然而，对于这些因素的相互关系，以及现有方法如何影响它们，仍缺乏深入理解。
3. 代理模型对可迁移性的影响：已有研究关注代理模型在对抗样本可迁移性中的作用。如攻击不同架构的代理模型集成可获得更通用的对抗样本更新方向；通过微调预训练代理模型获取中间模型用于集成。但尚未明确何种代理模型性能最佳，以及如何构建更好的代理模型来提升可迁移性。
4. 本文与已有研究的区别：本文在已有研究基础上，进一步深入分析对抗样本可迁移性，聚焦代理模型相关因素。不仅研究模型平滑度和梯度相似性对可迁移性的单独影响，更着重探讨它们的联合作用；深入分析数据增强和梯度正则化对可迁移性的影响机制；提出构建更优代理模型的通用方法，为理解和提升对抗样本可迁移性提供更全面、深入的视角 。

---

结论-Conclusion

该部分对全文研究进行总结，明确核心发现与贡献，同时提出未来研究方向，具体如下：

1. 核心发现与贡献
   • 解释“小鲁棒性”现象：通过理论和实验，深入探究对抗训练中的“小鲁棒性”现象，将其归因于模型平滑度和梯度相似性之间的权衡，并指出对抗训练中梯度差异是由流形外样本导致的数据分布偏移造成的。
   • 研究数据增强和梯度正则化的影响：系统研究数据增强和梯度正则化对可迁移性的影响。发现常用的数据增强方法会损害梯度相似性，且对模型平滑度的影响各异，最终导致可迁移性下降；梯度正则化普遍提高模型平滑度，但输入空间正则化在可迁移性方面不一定优于权重空间正则化。
   • 提出构建代理模型的通用方法：提出结合输入梯度正则化和锐度感知最小化（SAM）构建更好代理模型的通用方法，该方法能同时优化模型平滑度和梯度相似性，显著提升对抗样本的可迁移性，且可与独立于代理模型的方法集成，进一步提高可迁移性。
   • 分析各因素关系：通过相关性分析和回归分析，揭示模型平滑度和梯度相似性都与对抗样本可迁移性高度相关，且二者联合效应显著，不同对抗预算下应采用自适应的权衡策略。
   • 验证结论通用性：在商业机器学习即服务平台上的实验验证了本文结论的通用性，推翻了一些以往研究中关于对抗训练和数据增强与迁移攻击相关性的结论 。
2. 未来研究方向：尽管取得上述成果，但仍有诸多问题有待进一步研究。如进一步探索数据增强和梯度正则化影响可迁移性的内在机制；研究其他因素与可迁移性的关系，并将其与本文方法结合；深入探究SAM性能优势的原因，完善其理论基础等 。