matlab生成三维三次B样条曲线

在对无人机进行路径规划的时候，往往需要对规划的路径点进行平滑操作，目前用的比较多的就是B样条曲线，下面的matlab脚本文件是我根据别人写的python程序改编而来的，后文会慢慢说明代码结构。

clear;
clc;

% 定义控制点
x = [0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115];
y = [0, 0, 0, -1, -3, -4, -6, -8, -11, -12, -11, -11, -11, -11, -12, -13, -15, -18, -19, -21, -23, -22, -24, -24];
z = [-2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2];

n=length(x)-1;% B样条曲线有n+1个控制点
k=4;% 三次B样条，因此阶数=次数+1

% 用于储存生成的点
X=[];
Y=[];
Z=[];

Nik_u=zeros(1,n+1);% 用于储存基函数
nodevector=U_quasi_uniform(n,k);% 生成节点向量

for u=0:0.01:1-0.01% 循环次数决定组成B样条曲线点的总数量
    for j=1:n+1% 生成Bi,3这一系列基函数
        Nik_u(j)=BaseFunction(j,k,u,nodevector);
    end
    % 由于B样条曲线具有局部支撑性，因此只有u周围一定区间会参与到计算
    X=[X,x*Nik_u'];
    Y=[Y,y*Nik_u'];
    Z=[Z,z*Nik_u'];
end

plot3(X,Y,Z)

% 生成准均匀B样条曲线
function nodevector=U_quasi_uniform(n, k)
nodevector=zeros(1,n+k+1);% 节点数=控制点的个数+阶数
piecewise = n - k + 2;% B样条曲线的段数=控制点个数-次数
if piecewise==1% 只有一段曲线时，直接末尾重复度k
    nodevector(n+1+1:n+k+1)=1;
else
    for i=1:n-k+1% 中间段内节点均匀分布：两端共2k个节点，中间还剩(n+k+1-2k=n-k+1）个节点
        nodevector(k+i)=nodevector(k+i-1)+1/piecewise;
    end
    nodevector(n+1+1:n+k+1)=1;% 末尾重复度k
end
end

%定义第i个k阶B样条基函数
function Nik_u=BaseFunction(i, k, u, NodeVector)
if k==1% 定义Bi,0这一系列基函数
    if u>=NodeVector(i)&&u<NodeVector(i+1)
        Nik_u=1;
    else
        Nik_u=0;
    end
else
    % 公式中的两个分母
    denominator_1 = NodeVector(i + k - 1) - NodeVector(i);
    denominator_2 = NodeVector(i + k) - NodeVector( i + 1);
    % 如果遇到分母为0的情况，定义为1以便继续计算
    if denominator_1==0
        denominator_1=1;
    end
    if denominator_2==0
        denominator_2=1;
    end
    % 不断递归
    Nik_u=(u - NodeVector(i)) / denominator_1 * BaseFunction(i, k - 1, u, NodeVector) ...
    + (NodeVector(i + k) - u) / denominator_2 * BaseFunction(i + 1, k - 1, u, NodeVector);
end
end

B样条曲线的原理就不多说了，这里直接贴上我参考的文章链接 ：

B样条曲线_a useful man的博客-CSDN博客_b样条曲线

​​​​​​B样条曲线（B-spline Curves）_余生最年轻的博客-CSDN博客_b样条曲线

1、首先是要生成节点向量，由于我撰写本文的目的是方便无人机做路径规划，因此这里只考虑准均匀B样条曲线。生成节点向量需要路径点和曲线次数信息，其中n的大小取决于控制点的数量（n=控制点数-1），阶数k的大小取决于曲线的次数p（k=p+1 ）

% 生成准均匀B样条曲线
function nodevector=U_quasi_uniform(n, k)
nodevector=zeros(1,n+k+1);% 节点数=控制点的个数+阶数
piecewise = n - k + 2;% B样条曲线的段数=控制点个数-次数
if piecewise==1% 只有一段曲线时，直接末尾重复度k
    nodevector(n+1+1:n+k+1)=1;
else
    for i=1:n-k+1% 中间段内节点均匀分布：两端共2k个节点，中间还剩(n+k+1-2k=n-k+1）个节点
        nodevector(k+i)=nodevector(k+i-1)+1/piecewise;
    end
    nodevector(n+1+1:n+k+1)=1;% 末尾重复度k
end
end

针对我这个有24个控制点的轨迹，实际生成的节点向量是这个样子的 

 可以看到由于是3次4阶B样条曲线，因此节点向量的前后重复度为4，而中间等差数列的分母应该=总节点数-2*阶数+1，总结点数m+1=n+p+1+1（咱也不知道为啥m不能直接指代总结点数，n直接指代总控制点数，非要绕），在本例中，分母=21，因此从第5个节点开始，后面依次递增1/21。

2、得到了节点向量，接下来就要计算基函数了，根据这张经典的图，我们的最终目的是要计算Ni,3（i=0:23，总共24个，3取决于次数p=3）

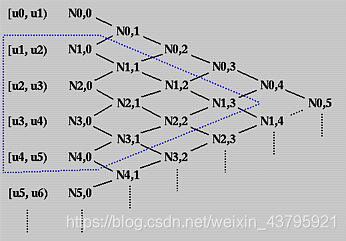
 而为了得到最上层的基函数，需要一层一层往下递推，若想得到N1,3，就要知道N1,2和N2,2，若想得到N1,2和N2,2，就要知道N1,1、N2,1和N3,1... ...根据下方公式，可以预见有时分母是0，会导致程序无法运算，因此根据大佬的思路，直接将分母定义为1从而使程序能继续运算。

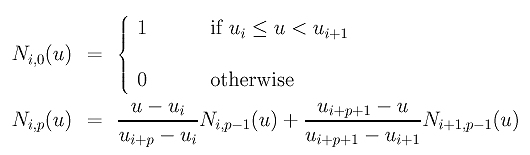
%定义第i个k阶B样条基函数
function Nik_u=BaseFunction(i, k, u, NodeVector)
if k==1% 定义Bi,0这一系列基函数
    if u>=NodeVector(i)&&u<NodeVector(i+1)
        Nik_u=1;
    else
        Nik_u=0;
    end
else
    % 公式中的两个分母
    denominator_1 = NodeVector(i + k - 1) - NodeVector(i);
    denominator_2 = NodeVector(i + k) - NodeVector( i + 1);
    % 如果遇到分母为0的情况，定义为1以便继续计算
    if denominator_1==0
        denominator_1=1;
    end
    if denominator_2==0
        denominator_2=1;
    end
    % 不断递归
    Nik_u=(u - NodeVector(i)) / denominator_1 * BaseFunction(i, k - 1, u, NodeVector) ...
    + (NodeVector(i + k) - u) / denominator_2 * BaseFunction(i + 1, k - 1, u, NodeVector);
end
end

3、有了节点向量和基函数，就可以构造B样条曲线了。由于节点向量就是将B样条曲线在[0,1]上的定义域按照一定规则分割，所以在实际计算曲线上每一点的位置的时候，变量u也得是在[0,1]上的，结果就是有几个u，画出来的曲线就有几个点。下图可以解释这种对应关系

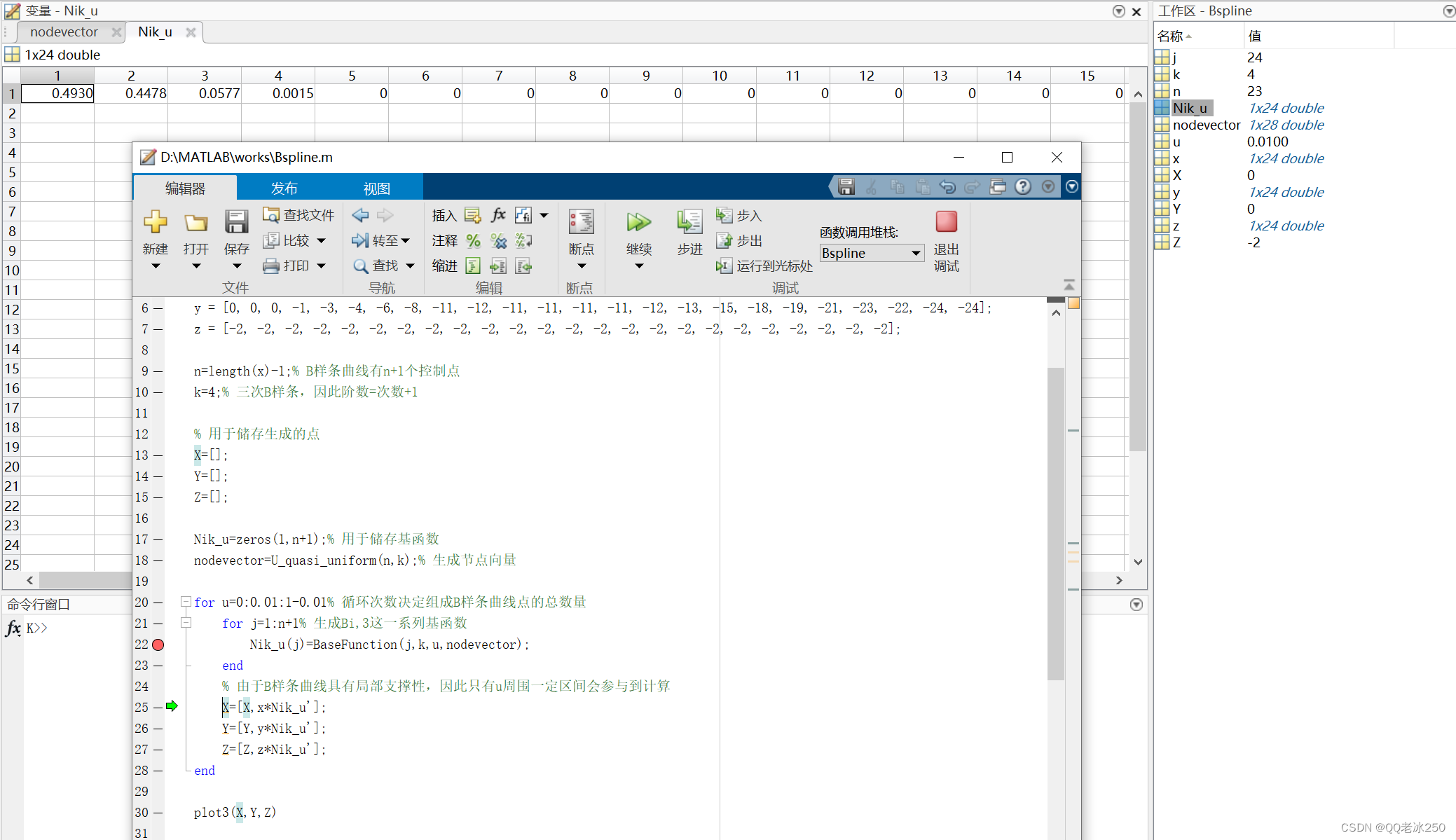
for u=0:0.01:1-0.01% 循环次数决定组成B样条曲线点的总数量

下图是当u=0.01时，所有的Ni,3（i=0:23），可以看到除了N0,3~N3,3有数值之外，其余基函数都是0，这就是B样条曲线的局部支撑性

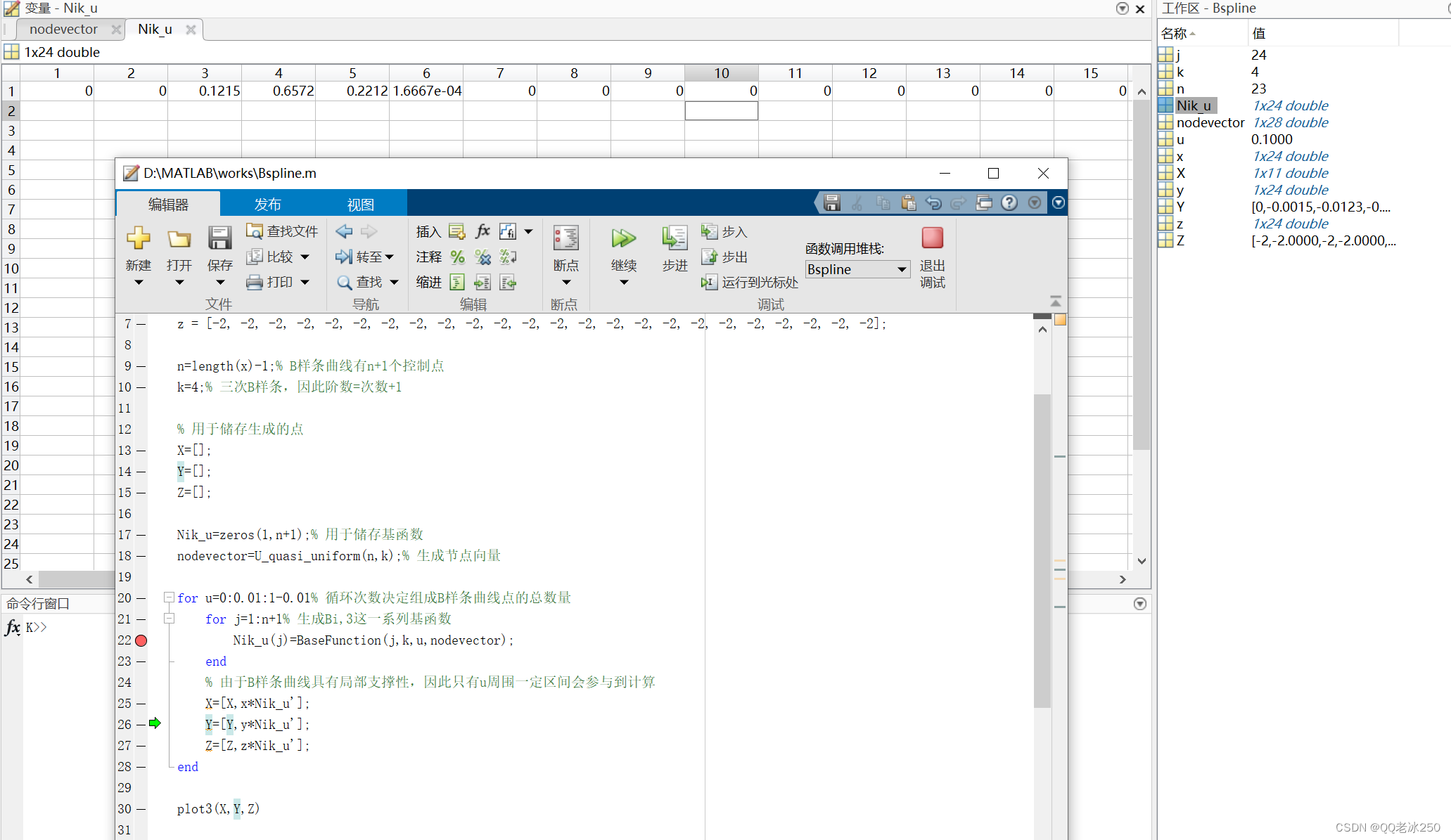
 当u=0.1时，这种效果就更明显了

 4、最终运行完就是这样的效果，我的控制点里z轴统一为2，所以看不出z轴上的变化，但其实改变z轴上的数值也是有效果的

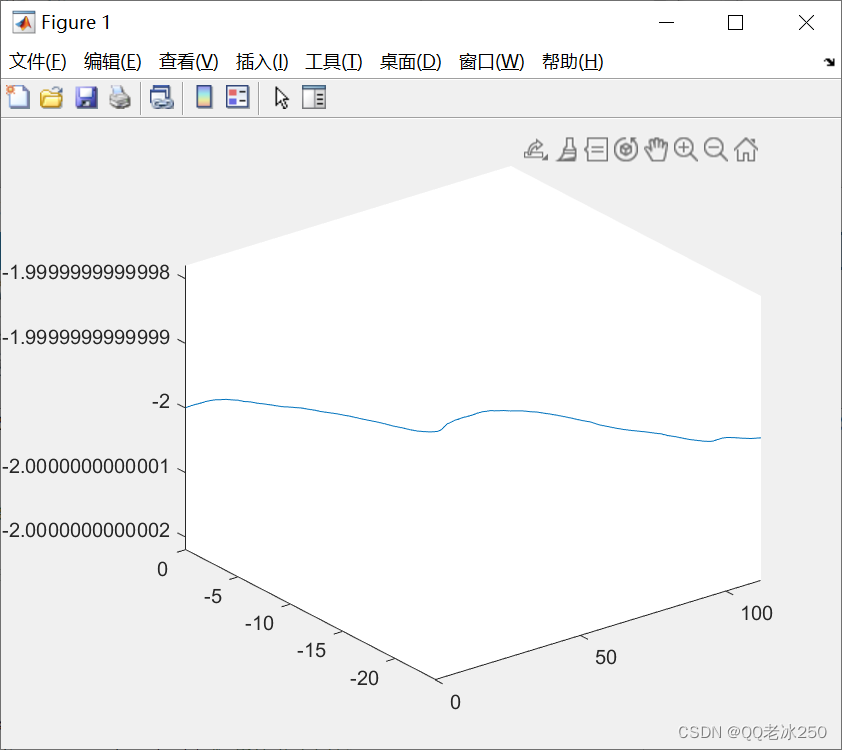
对于B样条曲线的理论部分其实我也没有理解的特别透彻，程序也是根据别人的代码然后按照自己的需求改过来的。不过有的时候，对于理解的理论，往往跟着现成的和理论配套的程序走一遍就理解了，我就是这么理解B样条曲线的，所以希望我的博客也能帮助到大家