非均匀三次B样条曲线插值实现及MATLAB代码

威威猫新手上路

已于 2023-06-20 09:57:27 修改

阅读量1w

点赞数 22

文章标签：几何学 matlab

于 2021-07-12 11:47:57 首次发布

本文链接：https://blog.csdn.net/qq_37866732/article/details/118671759

版权

本文详细介绍了非均匀三次B样条曲线插值的实现过程，包括插值点输入、控制点反算、节点矢量确定和基函数计算。通过MATLAB代码展示了如何利用追赶法求解三对角矩阵以及运用德布尔-考克斯递推公式计算基函数，最终得到曲线方程并进行插值点的拟合。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这篇博客跟我上一篇博客《均匀三次B样条曲线插值实现及MATLAB代码》的内容有点像，只是在基函数的计算上不同，造成均匀/非均匀的区别。

参考资料：

[1]（这个PPT讲得很通俗，但对于多插值点分段曲线的内容漏讲了一个知识点）三次周期B样条曲线的算法 - 百度文库 (baidu.com)

[2]（这个介绍只有两个插值点的三次B样条曲线，是B样条曲线最简单的形式了吧~）(7条消息) 从B样条的插值点反求控制点_cofd的专栏-CSDN博客

[3]（一本书，里面有讲到整体参数和局部参数设置、节点矢量划分等）《计算机辅助几何设计与非均匀有理B样条》

正文：

曲线插值一般指的是给定插值点，得出曲线的方程，曲线会经过所有的插值点。确定三次B样条曲线的输入量有两种，一种是给出控制点和其它边界条件，曲线一般不经过控制点；一种是给出插值点和其它边界条件，曲线会经过所有插值点，显然第二种输入量使用更为广泛，这里只介绍第二种情况。

①首先输入插值点，这些插值点可以是二维(x,y)点，也可以是三维(x,y,z)点，甚至更多维都可以，处理方法都相似，以二维点为例，MATLAB代码：

pointInput=[1 209.1;1.033 209.525;1.067 209.273;1.1 209.277;
    1.133 208.734;1.167 208.693;1.2 208.852;1.233 208.722;1.267 208.746;1.3 208.759];

这些点的分布如下图的红色拆线所示（不是蓝色的*型点，蓝色的是我最终拟合的曲线）。

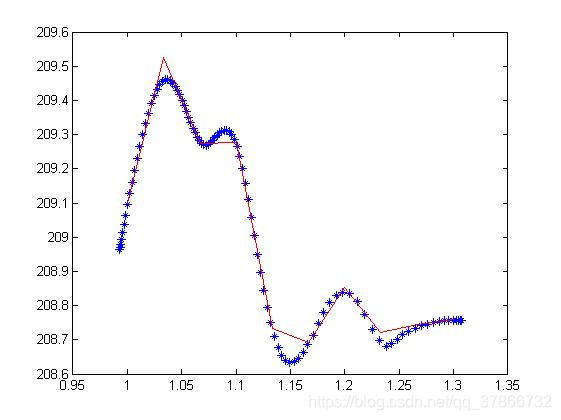
②计算N、n、k等值

N为插值点的个数，上面共有10个插值点，所以N=10。控制点个数为N+2个。n=N+1。k为次数，这里是三次B样条曲线，所以k=3。MATLAB代码：

N=length(pointInput);
k=3;
n=N-1;

③反算控制点

这里主要参考了资料[1]PPT中的内容，具体的请查看该PPT。三次B样条曲线的表达式（1）为

其中 $Q_{i}(i=1,2...N)$ 是第i段曲线的表达式， $t(t\epsilon [0,1])$ 是局部参数， $p_{i}(i=0,1...N+1)$ 是第i个控制点。注意节点、节点矢量、整体参数、局部参数的区别（具体的要看资料[3]或其它相关的资料了，说明这些可能需要长篇大论哦~）。