位运算用法小结

        最近在学计组，还在新手村（数据篇）的时候发现很多运算与思维都跟位运算有关系......

运算技巧

位运算库函数

231. 2 的幂

        1左移n位就是2的n次方（n = 0 1 = 2^0 , n = 1 2 = 2^1...... ）所以最直观的想法是：判断一个数的二进制数位是否只有一个1，剩下都是0即可。

class Solution {
public:
    bool isPowerOfTwo(int n) {
        int x = __builtin_popcount(n);
        return x == 1&& n > 0;
    }
};

        上述代码中 __builtin_popcount 用于计算一个数的二进制表达式中1的个数。

        一些常用的二进制函数：

函数	作用
__builtin_popcount（s）	返回 s的 二进制中 1 的个数
__builtin_clz(s)	返回s二进制数中的前导0个数（以无符号int为准，即总共32位） 所以一个数的二进制长度可以表示为 ： 32 - __builtin_clz(s)
__builtin_ctz(s)	返回s的二进制表达中的末尾0的个数

        但是我们也可以这样想： s = 1000 , s-1 = 0111。 此时 s&(s-1) 就为0了。 所以也可以这样判断：

class Solution {
public:
    bool isPowerOfTwo(int n) {
        return n>0 && (n&(n-1))==0;
    }
};

342. 4的幂

        直观想法： s的二进制表达式中 "1"的个数为1，且其后跟随的0的个数为偶数。

class Solution {
public:
    bool isPowerOfFour(int n) {
        if(!n) return 0;
        int one = __builtin_popcount(n);
        int zero = __builtin_ctz(n);
        return n>0 && one == 1 && zero%2 == 0;
    }
};

        同余思想： 4的幂一定是2的幂，2的幂不一定是4的幂。但是2^(2x) % 3 = 1; 2^(2x+1) % 3 = 2,其中2^(2x) = 4^x 所以先判断是否是2的幂，在判断%3的值是否等于1即可。

class Solution {
public:
    bool isPowerOfFour(int n) {
        return n > 0&&(n&(n-1)) == 0 && n%3 == 1;
    }
};

两种常用的&运算解释

191. 位1的个数

        可以直接用位运算的库函数 __builtin_popcount(x)。

        也可以用消除最后一个1的思想。 如何消除s = 10001010100的最后一个1呢？利用上面的方法： s - 1 = 10001010011 s & (s-1) 就是 1001010000 这样最后一位1就消除了。那为什么只会消除最后一位1，换句话说，为什么前面的1不会被消除呢？因为每次只减去了一次1，只会消除s中从后往前的第一个1，这样就可以通过统计1消除的次数来判断s中有几个1了。

class Solution {
public:
    int hammingWeight(uint32_t n) {
       int cnt = 0;
       while(n)
       {
           n &=(n-1);
           cnt++;
       }
       return cnt;
    }
};

        有没有什么方法可以一次性消除多个1呢？ 也是可以的。 s&(-s)即可消除除了从右往左第一位1以外的所有1。 我们通常把s = 101100中的最后一位1所表示的二进制数称为lowbit 。此时s的lowbit就是100 = 4。 如果求lowbit呢？ 当然可以利用__builtin_ctz(s)求出末尾0的数目再左移。更快的方法就是 lowbit = s&(-s)

---

s = 101100
~s = 010011

(~s) + 1 = 010100     根据补码的定义，这就是 -s 最低 1 左侧取反，右侧不变

s & (-s) = 000100

        为什么这样可以？ 因为计算机中存的是补码。当s>0 ，补码 == 原码 ；-s<0， -s存的就是s的反码+1，也就是010100,这样与s&完就剩下本位1了。

        计组中原码与补码的快速转换： 找到原码的从右往左数的第一个1，此1的前面所有数值位都取反。 所以补码的从右往左数第一个1的右边都是0 ， 与原码一样。 左边与反码一样。

  原码   101110 1 00 

  补码   010001 1 00

  反码   010001 0 11

        这样的话 ， 原码 & 补码 就是最后那一位1了，也就是lowbit.

异或运算的使用

面试题 16.01. 交换数字

        利用异或运算。

        什么是异或运算？简单一点说：二进制位相同为0，不同为1 

        更好的理解： 异或（XOR）运算 就是二进制不进位加法。

        异或运算满足的性质：

1） 交换律： a^b = b^a

2)   结合律：(a^b)^c = a^(b^c)

3)   自反性： a^b^b = a (b^b = 0,a^0 = a)

4)   a ^ a = 0 ; a ^ 0 = a (理解成二进制不进位加法就很好理解)

class Solution {
public:
    vector<int> swapNumbers(vector<int>& num) {
        num[0] = num[0]^num[1];
        num[1] = num[0]^num[1];
        num[0] = num[0]^num[1];
        return num;
    }
};

   解释：

        令a = num[0],b = num[1].

        a = a ^ b ;

        b = a ^ b = (a ^ b) ^ b = a ^ (b ^ b) = a ^ 0 = a

        a = a ^ b =  a ^ (a ^ b) = (a ^ a) ^ b = 0 ^ b = b  

136. 只出现一次的数字

        利用异或性质即可。由于两个数相互异或答案就是0，而0异或任何数都等于其本身，所以：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ans = nums[0];
        for(int i = 1;i<nums.size();i++)
            ans ^= nums[i];
        return ans;
    }
};

461. 汉明距离

        求的是两个数字对应二进制位不同的位置的数目。这不就是上面说的异或的概念嘛......

class Solution {
public:
    int hammingDistance(int x, int y) {
        return __builtin_popcount(x^y);
    }
};

与，或，非，移位运算

693. 交替位二进制数

        直观想法是：每次检查两位就行了，因为满足条件的情况只有：01，10。如果出现了00或者11就是错误的。

        如何检验呢？首先要明确的是：我们每次只想知道当前数的最后两位，前面的数我们是不需要的，也就是说 对于1110010，我们第一次想要的是0000010,第二次想要的是0000001。

        这里就要介绍一下|跟&去做掩码的写法了。

        & 运算：  Y = A & B

A	B	Y
0	0	0
0	1	0
1	0	0
1	1	1

      | 运算：  Y = A | B

A	B	Y
0	0	0
0	1	1
1	0	1
1	1	1

        ~(取反)运算 ： Y = ~A

A	Y
0	1
1	0

        从上表看出：

                 0 & 0或者1 答案都是0 ，0 | 0或者1 答案都是其本身。

                 1 | 0或者1 答案都是1 ， 1 & 0或者1 答案都是其本身。

        对于1110010 我们只想要后两位，所以我们直接&3（0000011）就可以了。

        那如何解决继续往后判断呢？只需要让 n 右移就行了。这样n = 0也结束了。

class Solution {
public:
    bool hasAlternatingBits(int n) {
        while(n)
        {
            if((n&3)==0 ||(n&3) == 3 ) return 0;
            n>>=1;
        }
    return 1;
    }
};

常用的位运算公式总结

面试题 05.01. 插入

        主观想法是将N的第i到j位全部清0，然后或上M就可以了（0或 任何数等于本身）

        如何清空呢？ 用0&就行了。但要保证其他位不变，怎么办呢？&1就行了。

        比如我们要让1011000的第5位的1变为0，我们只需要1011000 & 1101111即可。

        1 0 1 1 0 0 0 

    &  1 1 0 1 1 1 1

---

        1 0 0 1 0 0 0

        而1101111可以由 10000 取反而来，10000又可以由1左移4位而来。

class Solution {
public:
    int insertBits(int N, int M, int i, int j) {
        for(int k = i;k<=j;k++)
            N &= ~(1<<k);
        return N | (M<<i);
    }
};

        注意：二进制的表示中，是从0位开始数，与计算机的规则是一样的。所以左移x位就是x本事，不要去考虑+1，-1的问题。

        这里也摘录一些常用运算：

 判断奇偶：

        奇数： x&1 == 1 偶数 :x&1 == 0

 快速乘除2的n次幂：

        x >> n : x  /  2^n

        x << n: x * 2^n

 去除最后一位1： x & ( x - 1 )

 得到最后一位1： x & ( - x )

 判断是否是2的幂次： x & ( x - 1) == 0

 构造n个1： 1 << n - 1

 获取x的第n位值(0或者1)：( x >> n ) & 1 

 获取x的第n位幂值： x & ( 1 << n )

 仅将x的第n位置为1：x | (1<<n)

 仅将x的第n位置为0：x & ( ~ ( 1 << n ) ) 

 取反x的第n位： x ^ ( 1 << n )

从集合的角度去考虑二进制

参考灵神总结：https://leetcode.cn/circle/discuss/CaOJ45/

        二进制表示集合的优势： 二进制在计算机中的运算都是并行的，也就是说可以一下完成32个位的运算，这就提高了运算效率了。（类比加法器的串行与并行）。

        利用位运算「并行计算」的特点，我们可以高效地做一些和集合有关的运算。按照常见的应用场景，可以分为以下四类：

1. 集合与集合
2. 集合与元素
3. 遍历集合
4. 枚举集合

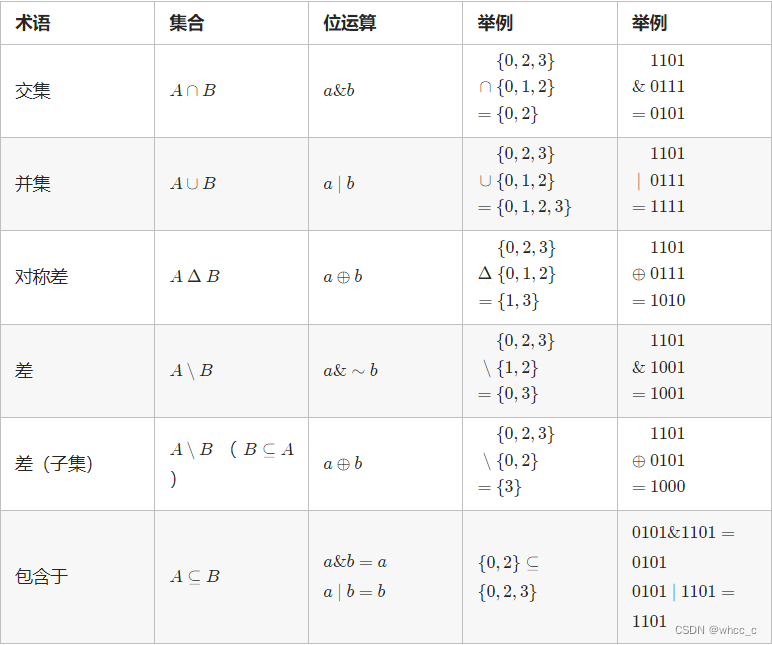
集合与集合

        常用的有 交集(&)，并集（|），包含和被包含

集合与元素

通常会用到移位运算。

其中 << 表示左移，>> 表示右移。

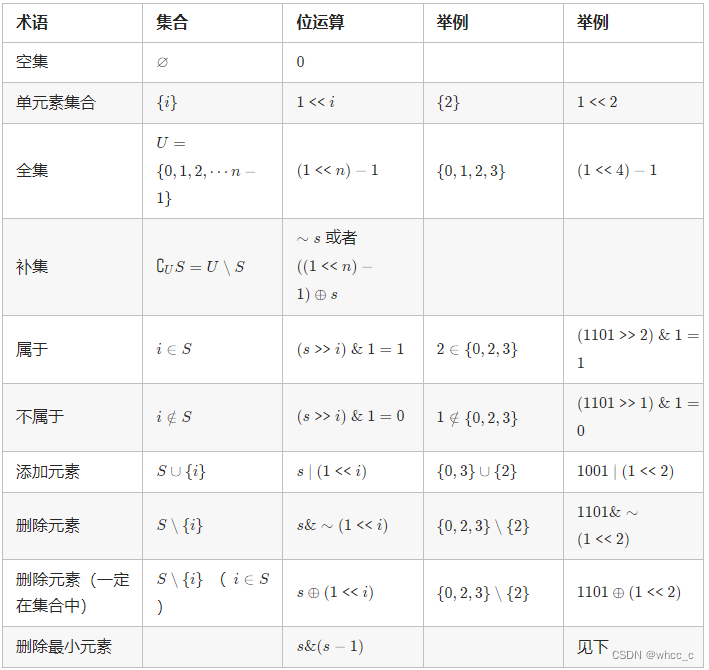
注意：

        ① 在写判断的时候判断s的某一位是否是1，一定要加上&1,如果只是(s>>i)的话，得到的是s除以2^i的值，并不是0或者1。而(s>>i) &1，由于0&上任何数都等于0，所以得到的就是s最低位是0还是1。

        ② 属于与不属于还可以写出 s & (1<<i) & 1（0）

        ③ 为什么构造全集是 （1<<n） - 1 ：比如说我们要构造一个集合，包括了0，1，2，3，4。一共有5位。1<<5后得到的是100000，-1之后是011111，这样就是构造初包含0-4一共5个元素的集合了。 位运算除了这里要-1，其他地方移位多少就是多少，不要考虑加减一。

遍历集合

        即遍历集合中所有的元素。

        设元素范围从 0 到n−1，挨个判断每个元素是否在集合 s 中:

#include<iostream>
using namespace std;

int main()
{
	int s = 254; // 11111110
	int n = 8;
	for (int i = 0; i < n; i++) // n是集合的长度，11111110长度为8
		if ((s >> i) & 1)
			cout << i << endl; // 具体逻辑
	return 0;
}

枚举集合

        遍历集合是遍历的是集合中的元素，但是集合中也包含了其他的集合，如何枚举集合呢？

        设元素范围从0到n-1，从空集∅枚举到全集U：

for (int s = 0; s < (1 << n); s++) {
    // 处理 s 的逻辑
}

        设集合为 s，从大到小枚举 s 的所有非空子集 sub：

for (int sub = s; sub; sub = (sub - 1) & s) {
    // 处理 sub 的逻辑
}

        这种写法跟上面常用&运算一样，只是设了一个中间变量sub。

78. 子集

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> ans ;
        int n = nums.size();
        int s = (1<<n)-1; // 构造全集
        for(int sub = 0;sub <=s ;sub++) // 遍历所有子集
        {
            vector<int> t;
            for(int i = 0;i<n;i++) // 遍历子集所有元素
                if(sub &(1<<i)) // 判断该位置元素是否存在
                    t.push_back(nums[i]);
            ans.push_back(t);
        }
        return ans;
    }
};

77. 组合

class Solution {
public:
    vector<vector<int>> combine(int n, int k) {
        vector<vector<int>> ans;
        vector<int> t;
        int s = (1<<n) - 1; // 构造全集
        for(int sub = 0; sub <= s;sub++)  // 枚举子集
        {
            t.clear();
            int cnt = __builtin_popcount(sub); 
            if(cnt == k) //只有子集中元素个数=k的才去讨论
            {
                for(int i = 0;i<n;i++)  // 枚举元素
                    if((sub>>i)&1) // 这一位存在再放入答案
                        t.push_back(i+1);
                ans.push_back(t);
            }
        }
        return ans;
    }
};

补充两道题：

137. 只出现一次的数字 II

        在只出现一次的数字中，我们通过异或运算，由于a^a=0的性质，一直异或就可以得到最终只出现一次的数字。但如果其他的数字都出现三次了呢？

        异或的本质： 二进制不进位加法。数位只有0，1两种状态。其实就是对答案mod2了。那如果一个数出现三次，那它某一位如果是1，三次相加以后一定是3，我们直接mod3不就好了？

        所有现在我们只需要统计32个位，对每个数的二进制表示的每一位进行加和，最后再mod3，最终得到的就是那个只出现一次的数。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ans = 0 ;
        for(int i = 0;i<32;i++)
        {
            int cnt = 0; 用来统计每一位上所有数二进制的1总和
            for(int num:nums)
                if((num>>i)&1)
                    cnt++;
            ans |= cnt%3 << i ;
        }
        return ans;
    }
};

260. 只出现一次的数字 III

直接上灵神思路了。

其实那一位也不一定是lowbit，也可以是其他位的1，但一定至少存在一个1。

        两种求lowbit的方法： 第二种求完直接与运算就可以了。相当于移位过了

        lowbit == 1 << __builtin_ctz(t)

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        int t = 0 ;
        for(int i : nums) t^=i;
        int lowbit = __builtin_ctz(t);
        int x = 0,y = 0;
        for(int i: nums)
        {
            if((i>>lowbit)&1)
                x^=i;
            else y ^=i;
        }
        return {x,y};
    }
};

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        unsigned int  t = 0 ;
        for(int i : nums) t^=i;
        int lowbit = t & -t;
        int x = 0,y = 0;
        for(int i: nums)
        {
            if(i&lowbit ) x^=i;
            else y ^=i;
        }
        return {x,y};
    }
};