离散数学·集合论【等价关系和序关系】

练习放在文末

模n同余关系

模上n，得出的余数是相同的（重点在余数）

例子

just scan 

等价关系

首先R是AA卡氏积的一个子集，然后R满足自反，对称和传递

等价类

[x]是所有与x满足关系R的元素的集合

定理

商集

例子

  

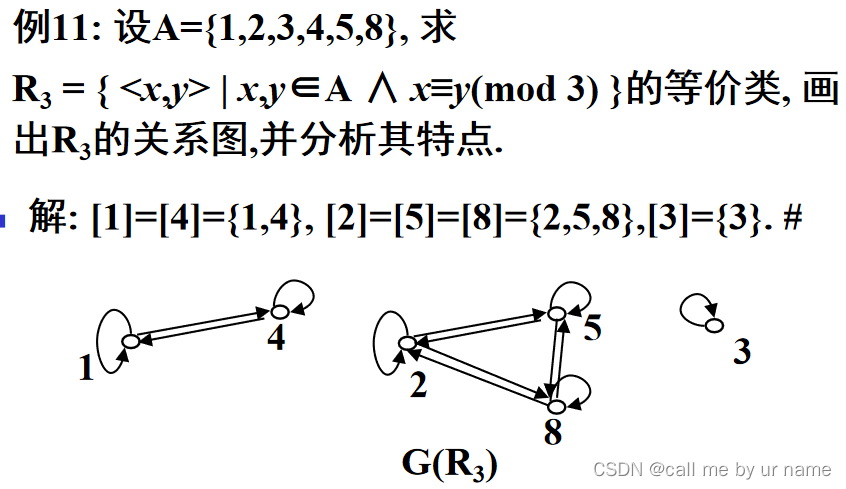
满足R关系的所有等价类的集合

划分

义如其名——就好比一个关系图里，一块一块的区域被划分了。花A是P(A)的一个子集

空集不是它的元素

元素不相交

例子

正如划线句子所描述的：

每个划分对应一个等价关系

当进行完划分后，需要用等价关系的形式描述这个划分 

等价关系与划分是一一对应的

等价关系是划分；A被划分成很多块，花A就是此时的划分，RA是A的等价关系，然后x,y共属于A上的一个被划分的块，且x,y满足等价关系。同块关系是一个等价关系。

划分的加细

有点类似子集，花A的每一个划分块都能被花B的某个划分块涵盖（花B将A划分为一个大的块——A本身。花A就无论如何都是花B的一个加细）

偏序关系

主要是R要为反对称。（不要用小于等于这个特质来记忆这个概念，就只要知道偏序关系满足自反、反对称、传递）而R中元素有点类似小于等于的关系（x不能在y的后面，即有（x,y）不能有（y,x））（R为有序对的集合）

注意：没有要求偏序集中的元素都是可以比较的，正所谓不要用小于等于这个特质来理解

全序关系

首先，对于偏序集。其次，任意的y与x是可以比较的（也就是在哈斯图中，任意的元素都直接或间接地相连）

拟序关系

记住反自反，反对称，传递

定理

定理

三岐性

与上面定理不尽相同（上面定理指出至多一项成立，而三岐性要求必须有一项成立），（个人看法）三岐性要求拟序中每一项都可比。

拟序应该也不是重点

哈斯图

画哈斯图的规则

例子

最大元、最小元

首先，y是属于B的。然后，在B内y能与所有元素比较，才能算是最大（小）元（否则不存在最大（小）元）

极大元、极小元 

大体上跟最大（小）元相同。唯一区别：极大（小）元是可以出现元素无法比较的情况，此时该元素既是极大元，又是极小元。 

上界、下界

跟最大（小）元不同的是：y属于A（也就是全定义域的最大（小）元）（仍然是要求y能与所有元素比较）

上（下）界其实本身就包含了最大（小）元的意思，所以同样要求能与所有元素进行比较（为了方便记忆）

最后就是区域内最大（小）元加上整个集合内最大（小）元（如果是重叠的，只算作一个，并不是说上界的数量是定的） 

上界应该都是存在的，但可能非常大。

上确界、下确界

要求的是上（下）界的最小（大）元素

练习

34题（1）（2）

题目应该是省略掉了合成符号 

37题

（应该是）如果给定具体的集合（类似题目中的A，而且给定具体运算）时，可以用易知来直接回答等价关系

商集是等价类的集合

39题

不难，但是通过题目来应用商集和等价关系的知识

41题

不难，但是足够经典

50题

类似41题

还是动手写写，其实看着是很简单，但是实际实践时，才会发现问题，有时候是懂那个意思，却不知道如何表达

这个反对称值得再写一下