数字逻辑·逻辑代数【常用公式、化简】

call me by ur name

已于 2023-02-24 18:44:59 修改

阅读量1.3w

点赞数 18

文章标签：算法

于 2022-09-29 23:12:07 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_61786525/article/details/127095827

版权

本文深入探讨了逻辑代数的基础，包括分配律、德·摩根定律、对偶原理和各种定理。通过实例展示了逻辑函数的化简方法，如卡诺图化简，强调了在解决实际问题中灵活运用这些概念的重要性。此外，还提醒读者在做题时要能够迅速识别并应用相关定理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

目标

掌握逻辑函数三种常见表现形式之间的关系
掌握逻辑代数的基本公式
掌握逻辑代数的主要定理
掌握逻辑代数的常用公式
掌握逻辑函数的代数化简方法
熟练掌握逻辑函数的卡诺图化简方法

提纲

分配律、德·摩根律、对偶、展开定理、吸收律、包含律
逻辑表达式化简
卡诺图化简

内容

逻辑函数的三种表现形式

真值表、逻辑表达式、卡诺图

相等

在这里插入图片描述

一些定律

在这里插入图片描述

仔细看看分配律和德·摩根定理
看似简单，但是用处很大。看看就行了，里边内容都是知道的，只是在做题的时候要反应过来有这么一个定理即可

对偶

在这里插入图片描述
只换常量和运算符，其他的不变

注意运算顺序不变2024.2.24复习

展开定理

在这里插入图片描述

对于 · ，提取出来的x_i，正为1（因为是积的运算，所以是x_i · 1 = x_i），非为0（相反）
对于 + ，提取出来的x_i，正为0（因为是和的运算，所以是x_i + 1 = x_i），非为0（相反）

吸收律

在这里插入图片描述
其实，这上面的公式都可以推导出来，但是做题的时候不一定能反应过来

包含律

在这里插入图片描述
这个公式主要是从逻辑上推导，出现 A·B+~A·B时，B·C=0，因为，A是和B同时出现的，而 ~A是和C同时出现的，但不可能同时出现A和 ~A，所以B和C是不能同时出现的

化简

在这里插入图片描述
注意第3个消元，我真的，我哭死。求求了要记住😭😭😭😭

例题

在这里插入图片描述
不是一昧地缩减，在算式前期也需要利用公式增加项辅助运算

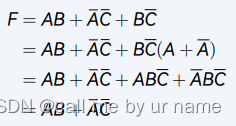
这个就是包含律，没什么好说的😋😋😋

这个可以多看看，有点绕

看了上面的，这个题感觉还行😊😊😊

也还行

卡诺图化简

在这里插入图片描述

老师的建议是记住，那么我还是记住吧🤗🤗🤗
重点在于卡诺图的下标顺序 0——1——3——2 （后面2位是反的，后面的行以此类推）

看文字规则，会发现，根本不知道在讲什么😇😇😇
下面还是看一些例子，帮助理解
在这里插入图片描述

不难看出

首先，做出完整卡诺图
接着，圈起部分极小项（对应左上角要求的表达式）

作业

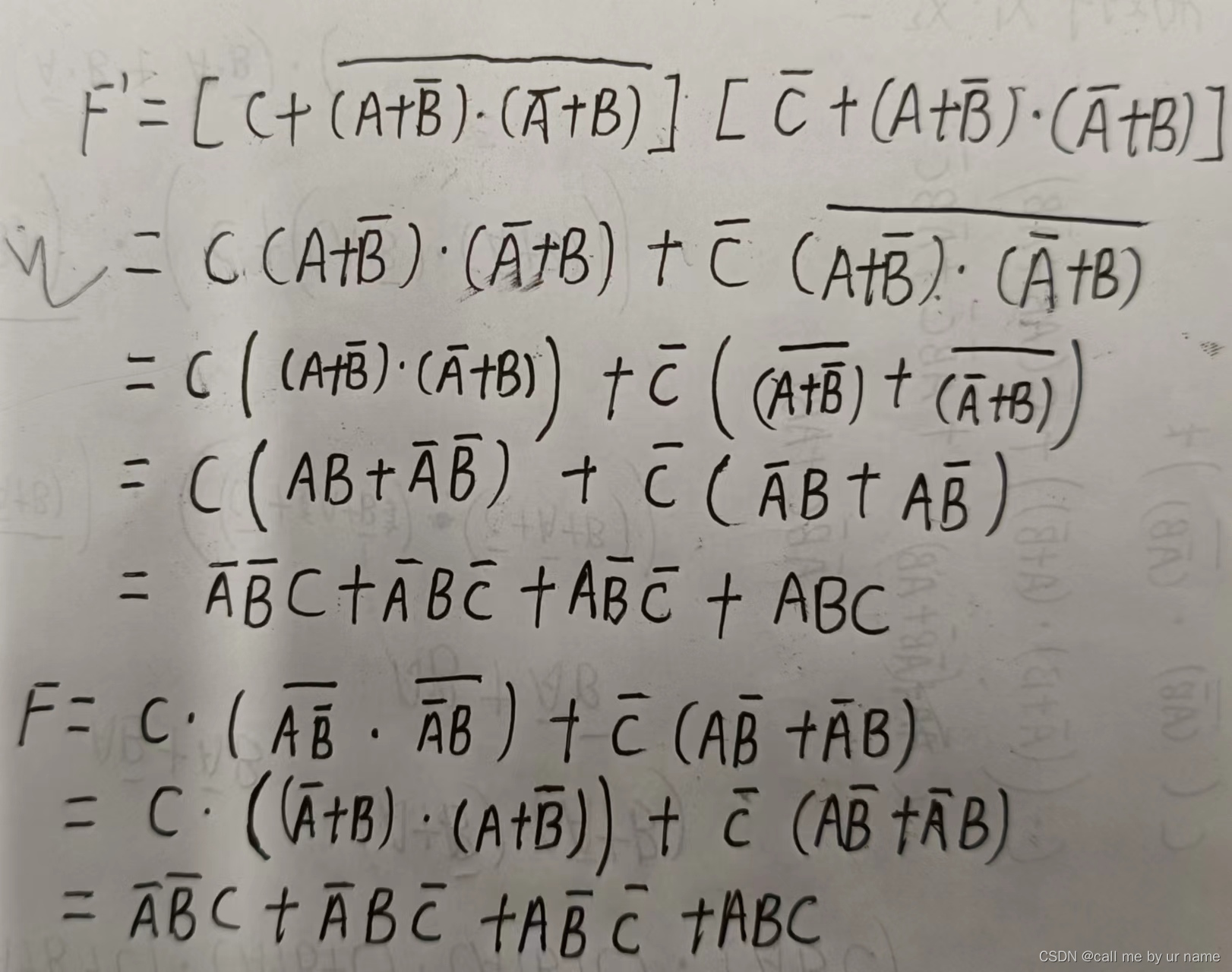
在这里插入图片描述

解

在这里插入图片描述

这道题还是有点复杂的，建议好好看看

评论 1

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。