大学物理·第5章【静电场】

call me by ur name

已于 2022-11-14 20:32:21 修改

阅读量1.5w

点赞数 20

文章标签：学习

于 2022-09-06 22:26:09 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_61786525/article/details/126734945

版权

这篇博客主要探讨静电场中的关键概念，包括点电荷电场强度分布、电偶极子的电场、高斯定理及其应用。内容涵盖电场强度通量、电势能、电势和电场强度的关系，并通过例题解析电场强度的计算及电势差的确定。此外，还涉及无限长导线的电场强度问题和电通量矢量的计算。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

电场强度

点电荷电场强度分布

在这里插入图片描述

多个点电荷在某点处形成的电场强度

在这里插入图片描述

电偶级子的电场强度

在这里插入图片描述

电偶极矩的方向——由负指向正
2022.11.06期中复习

例题

在这里插入图片描述

主要是E_垂直是相互抵消的，所以不计
2022.11.07期中复习

电场强度通量、高斯定理

在这里插入图片描述

闭合曲面上的通量

点电荷位于球形高斯面

中心

在这里插入图片描述

位于高斯面任意位置

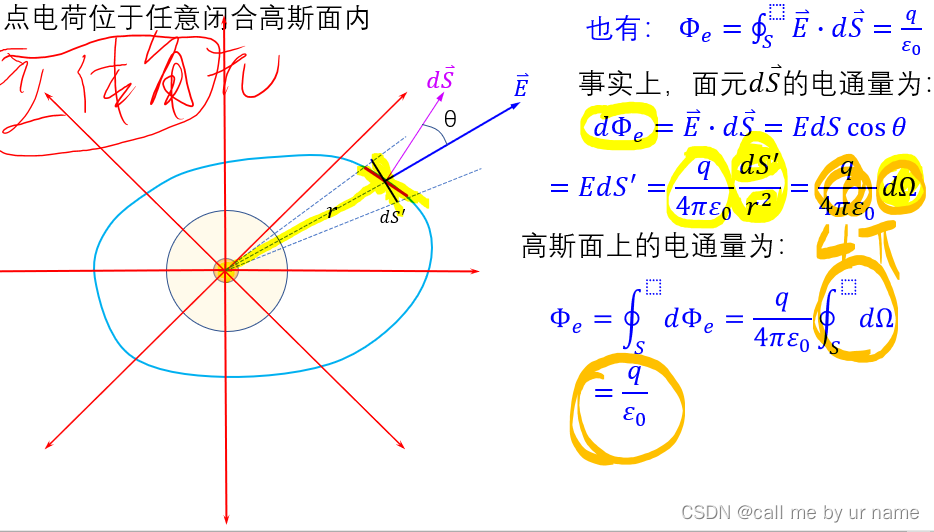
在这里插入图片描述
立体角 —— （球）面积/半径的平方——4π，在球内任意一点都是

其他情况

在这里插入图片描述
比较简单，如果一条电场线出入是成对的，那么电通量就是0
不是成对的话，一般就是q/ε₀

电荷系的电通量

在这里插入图片描述
也很好理解，由上文可知：点电荷在曲面外的电通量就是0，那么只用考虑内部的电荷，每个点电荷产生的电通量用上文的公式计算，再积分和 ∫ 即可

总结

在这里插入图片描述

高斯定理的应用举例

在这里插入图片描述
球面内，~~根据对称性，易知——内部电场强度=0~~ ，内部电荷为0，所以电场强度为0
球面外，可以这样理解——将均匀带电球面看作带电点电荷，再运用上文学过的静电场高斯定理，即可知道结果

球体

在这里插入图片描述

图同上文的球面，但是球体内部电场强度非0

例1

在这里插入图片描述

带电平面所带电场强度 —— E=σ/ε₀
这道题不必🙅‍过于深究2ES中的2了，看到题目这样，简单地想到就是对称性，有2个E

电势能

在这里插入图片描述
其实，这一页不是很重要，因为后面用不到这个公式😐😐😐
只是知道一下，与路径无关，只与始末位置有关即可

静电场的环路定理

在这里插入图片描述
对于闭合回路做功显然为0😶😶😶
这个公式和后面的不太一样，别搞混淆了

电势

在这里插入图片描述
注意始末位置
因为沿着电场线的方向，电势逐渐降低，所以初位置--末位置是正数

计算点电荷电场中场点的电势

在这里插入图片描述

这个公式其实也好推——因为在上文出现频率极高并且需要掌握的公式是通量 = q/ε₀ = ∫ EdS。由此易知：E=q/4πε₀r² e_r （其中，e_r为方向矢量）

故，V_A（A的电势）如此

叠加原理

在这里插入图片描述
电势是标量，所以无需矢量和，直接相加即可

例题

在这里插入图片描述
主要需要注意的是——在半径之内的电场强度为0，所以电势不变，电势差为0。但场强为0，电势不一定为0

注意e_r·dl为dr

这题主要注意不能选择无限远为0，至于具体怎么判断，就看取无限远时会不会不收敛

电场强度与电势梯度

在这里插入图片描述

公式

在这里插入图片描述

老师说过的：方向导数是梯度在这个方向上的投影

所以只需记住，E=-电势在这个方向上的投影

例题

在这里插入图片描述
注意 << 的使用

这里主要是看看公式的实际用法

练习

选择

在这里插入图片描述

证明表达式

在这里插入图片描述

一开始看到这道题没什么思路，但其实很简单（可能是太久没学物理导致的😮😮）
根据题目信息列出相关公式即可

题解

题目中有动能，就想到动能定理
因为绕圆轨道，想到向心力的公式，再结合一下1中列出的动能定理，所以应该是qE=mv²/2
发现题目最后问的v²是不带r的，所以还要找公式（仍然从向心力公式中演变，因为根据题目的信息只能使用这个）
结合2中演变的公式，消去r即可

无限长导线的电场强度

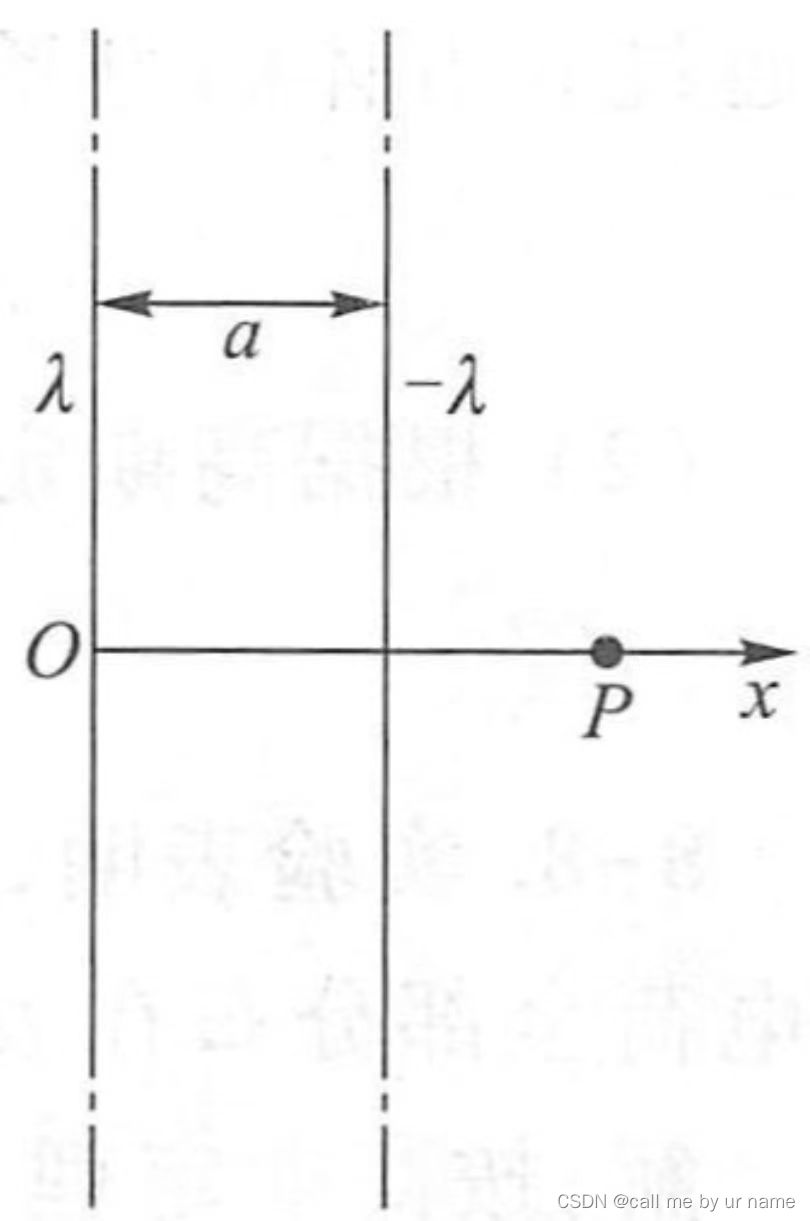
在这里插入图片描述

这道题先自己看看第1问，相信我，你不会写的🌯🌯🌯2022.11.07期中

电通量矢量

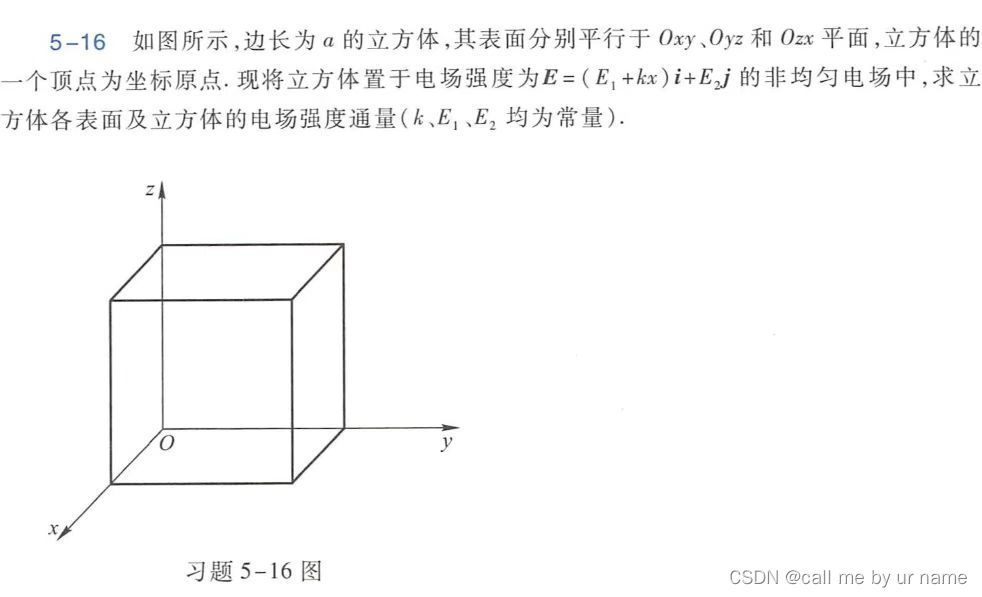
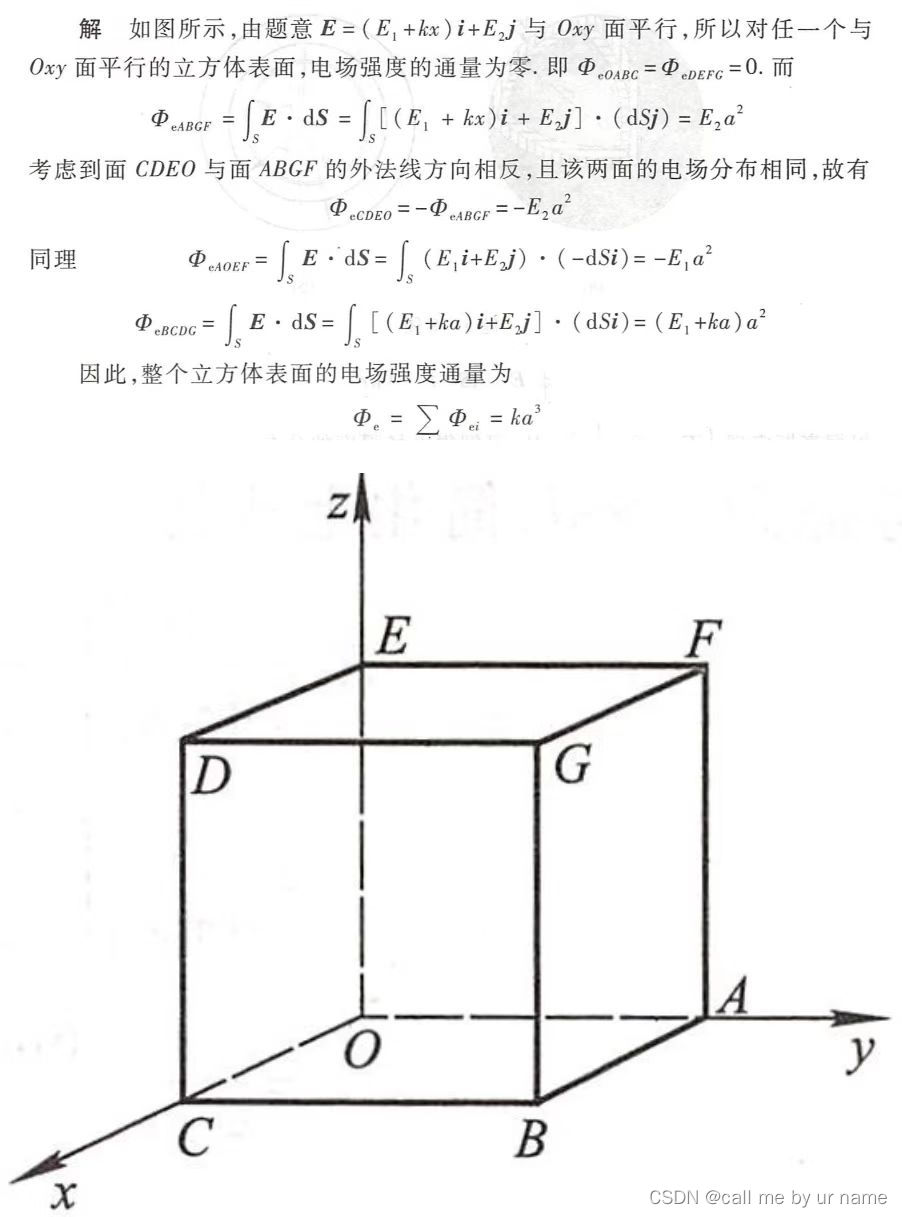
在这里插入图片描述

这题不会写，问题主要是不清楚矢量的关系（虽然看了很多，但没用🥫🥫🥫）

i表示x轴方向，j表示y轴方向
所以平面_ABCO和平面_FGDE的电通量=0
平面_ABGF和平面_OCDE是∥x轴的，所以 i 方向的电通量=0

当dS无法表达时

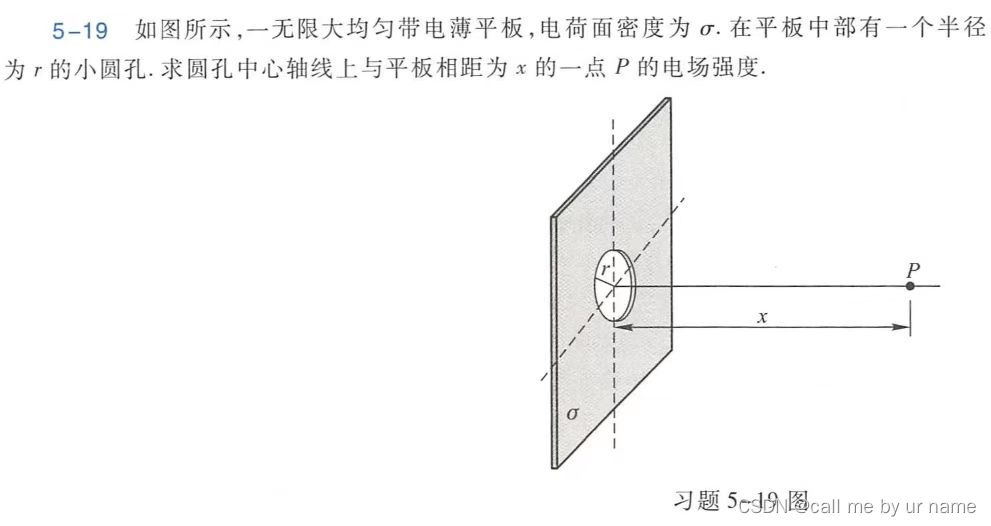
在这里插入图片描述

补偿法 上课讲过，在做的时候想到了
做题的时候想着用E=1/4π……的那个公式，但是无法表达dS
答案给的是用高斯定理，巧妙避免了dS的问题🍖🍖🍖
至于为什么用高斯定理求出来的电场强度一直是匀强的，我不理解

高斯定理

在这里插入图片描述

别的不说，这道题好好看看，真的要掌握高斯定理的用法

取高斯面（r<R）
取高斯面（r>R）

与无限长电导线的区别

在这里插入图片描述

这题的电场强度没有使用 λ/2πr + λ/2π(R-r)

求电势

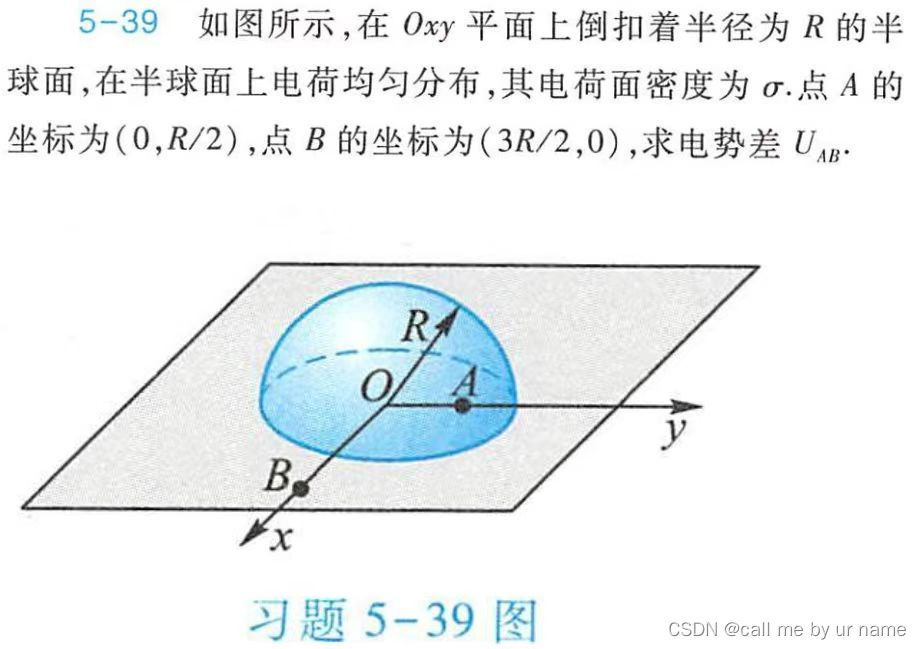
在这里插入图片描述

首先补成完整球面
也可以高斯定理先求电场强度，然后用电场强度 Edl 算（结果一样）

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。