写在最前面,题目给的问题如果可以用反证法,那么直接反证法(或者说首先考虑反证法)
定义

说明

无向图

多重集 —— 集合可以出现重复元素
V不能是空集——不能没有结点
圆括号代表没有方向
有向图

尖括号代表有方向
一些其他图

零图——有多个点的图(没有一条边)
平凡图——只有一个点的图(没有任何边)
标定图、非标定图、基图

看看就行
相邻、关联

注意区分相邻和关联
关联——点与边
相邻——点与点,边与边
环——就是自环后面学习的时候,看到环总是不知道什么意思🍜🍜🍜
有向图方向相同的才是平行边(所以那个紫色的不是平行边)
邻域
对于无向图

邻域——所有相邻的点组成的集合
顶点的度

最大度、最小度

主要看看最大度和最小度
握手定理

这个很好理解,一条边对应两个点(就有2个度数)
顶点度数和=边数的2倍
问题

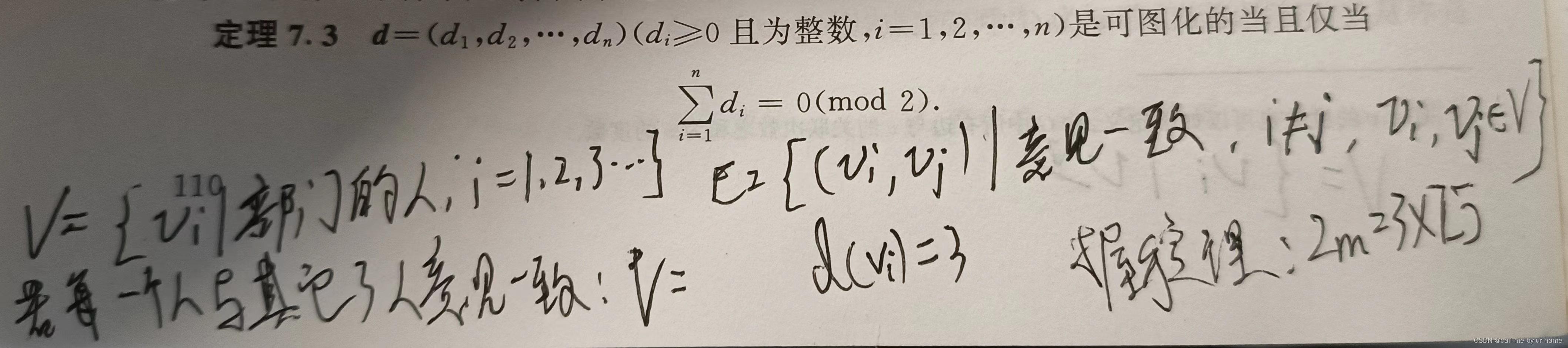
反证法
简单图、正则图

无向简单图,最大度△≤n-1发现用得还是挺多的
==无向简单图,最小度δ+1≤n
性质
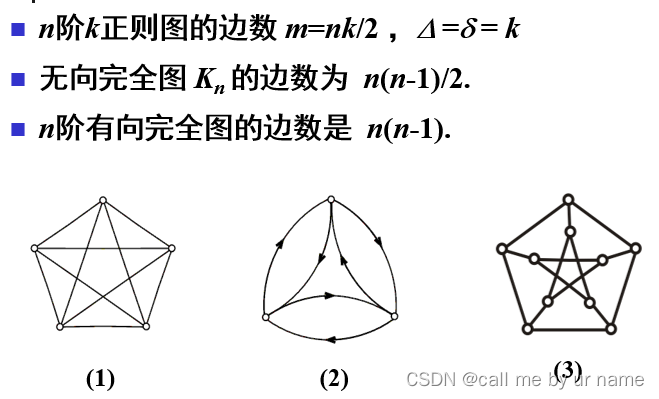
Kn边数有涉及到稍微看一看即可2023.2.11复习
度数列

可图化、可简单化

可图化要求满足握手定理2023.2.11复习
可简单图化还要满足有偶数个奇数
定理

可图化要求度数总和为偶数
Havel定理

- 度数列是有顺序的 从大到小 排列
- 最大的度数不能超过 n-1
- 如果dd1+1与dn是同一个的话,在d’中是取dd1+1-1
- 如果看不出来,就一直递归,直到度数列首项出现0(意味着可简单图化)
若出现负数,则不能简单图化度数列全为0时,可简单图化
havel定理的算法(辅助理解)
bool figure::Havel() {
for (int i = sizeof(point_d) - 1; i >= 0; --i) {
sort(point_d, point_d + i + 1);
if (!point_d[i]) break;
for (int j = i - 1; j >= 0 && point_d[i]; --j) {
--point_d[j], --point_d[i]; //这里比较关键,i对应的是最大的数,如果j对应的后面的数不能使最大的数减为0,就说明一定存在平行边
if (point_d[j] < 0)return false;
}
if (point_d[i] > 0) return false;
}
return true;
}
havel定理适用于无向图
havel定理要从小到大排序
子图

子图——点集、边集是原图的子集
注意看一下生成子图、导出子图
生成子图:
- 点集=母图的点集
导出子图:
- 由边导出的子图,给出一些边,根据这些边在母图中的关联关系得到点集
- 由点导出的子图反之
补图
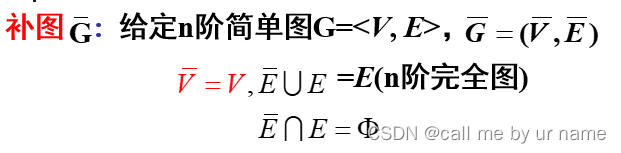
补图——与原图合并起来就是 完全图
自补图 —— 补图与自身相同
相对补图

与 补图 不同的是,是给出2个图,用最大的图减去小图(减去的包括边和点),得到的图就是 相对补图
图的同构

定义,这部分先别硬看了,难以理解
先看例子
例

简而言之——形状可以随意变化,但是点与边的关联,点与点的相邻不可以变


Ramsey问题(拉姆齐问题)



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








