逻辑函数的化简

 一个逻辑函数可以写成不同的表达式形式，表达式越简单，所表示的逻辑关系越明显。化简逻辑函数的目的，就是为了降低系统的成本，提高电路的可靠性，以用最少的逻辑门实现逻辑函数。

1.公式法化简

• 并项法

运用  AB+AB'=A(B+B')=A  ；可以消去一个变量。

例如：Y= ABC+ABC' = AB

•  吸收法

运用  A+AB=A(1+B)=A  和 AB+A'C+BC=AB+A'C

例如：Y=(AB)'+A'D+B'E =A'+B'+A'D+B'E = A'+B' = (AB)'

• 消去法

运用  A+A'B=A+B  或  A'+AB=A'+B

例如：Y1=A'+AB+B'C = A'+B+B'C = A'+B+C

• 配项法

将函数某一项乘（或）A+A'=1，将一项变两项。或利用 AB+A'C+BC=AB+A'C

例如：Y=AB'+A'B+BC'+B'C = AB'+A'B+BC'+B'C+A'C = AB'+BC'+A'C

 

试将以上几点综合运用：

Y1=AD+AD'+AB+A'C+BD+ACEF+B'E'+DEF

    = A(1+B+CEF)+A'C+BD+B'E+DEF

    =A+A'C+BD+B'E+DEF

    = A+C+BD+B'E+DEF

    = A+C+BD+B'E;

Y2=AC+A'D+B'D+BC'

    =AC+BC'+(AB)'D+AB

    =AC+BC'+D

 

---

2.逻辑函数的卡诺图化简

• 卡诺图

相邻最小项：两个最小项中只有一个互为反变量，其余变量相同，简称：相邻项。相邻项可合并为一项。

卡诺图的组成及特点：

①  n个变量的卡诺图由2^n个小方格组成，每个小方格代表一个最小项，按照循环码（格雷码）的编码顺序排列。

②  变量的坐标值0表示相应变量的反变量，1表示相应变量的原变量(且该坐标值使该方格对应的最小项取1)，当你将卡诺图中所有的1方格对应的最小项直接相加时，你确实可以得到一个逻辑表达式，但这个表达式往往不是最简的。

③  卡诺图上处在相邻、相对（即同行或同列的两端）位置的小方格所代表的最小项为相邻最小项。可以从图形上直观地找出相邻最小项。两个相邻最小项可以合并为一个与项并消去一个变量。

二变量卡诺图：

 

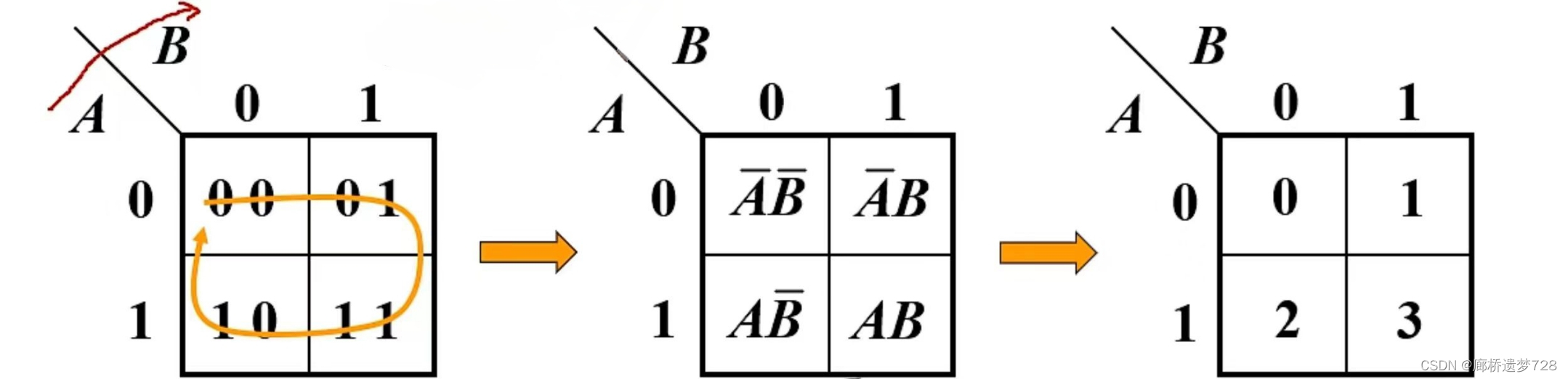
三变量卡诺图：

 

 

四变量卡诺图：

 

 

 

• 用卡诺图表示逻辑函数

基本步骤：

（1）求逻辑函数的真值表，标准与或式 或 一般表达式；

（2）根据变量个数画卡诺图；

（3）根据真值表，标准与或式 或 一般表达式 填写卡诺图；

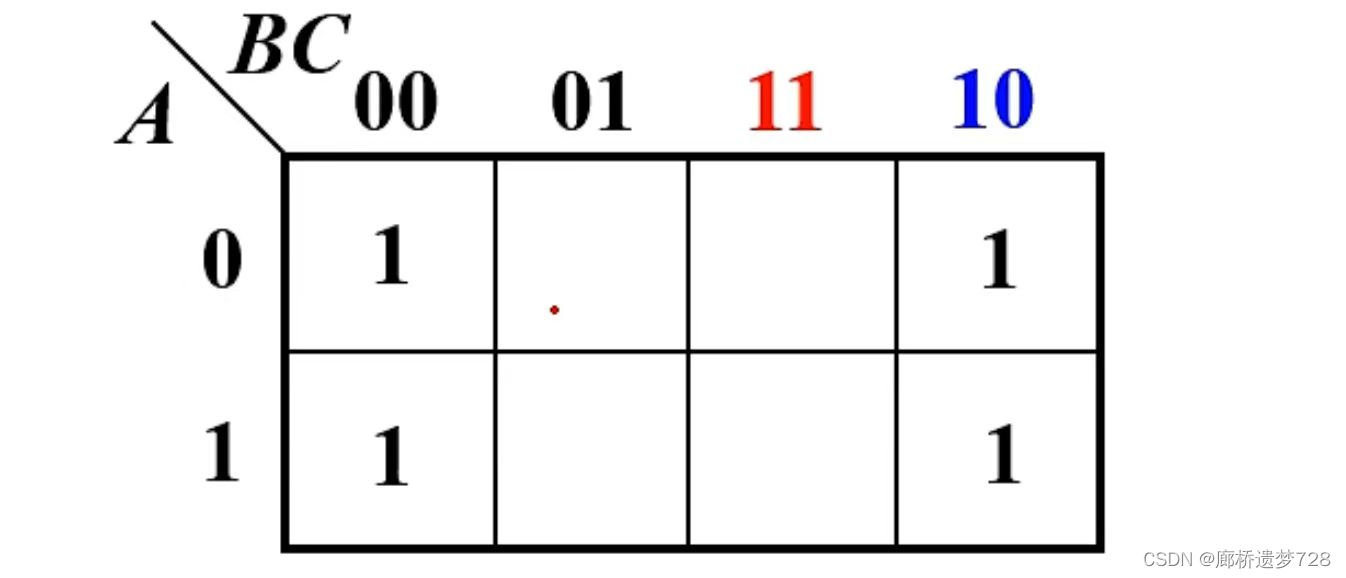
对真值表：找到表中为 “ Y=1 ” 的最小项，在卡诺图相应方格中填 “1” ，其余不填。（卡诺图其实就是一个变相的真值表。）

A	B	C	Y
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	0

例如将此真值表转换为卡诺图

 

 

 

 对标准与或式：将式中最小项对应方格填 “1” ，其余不填。

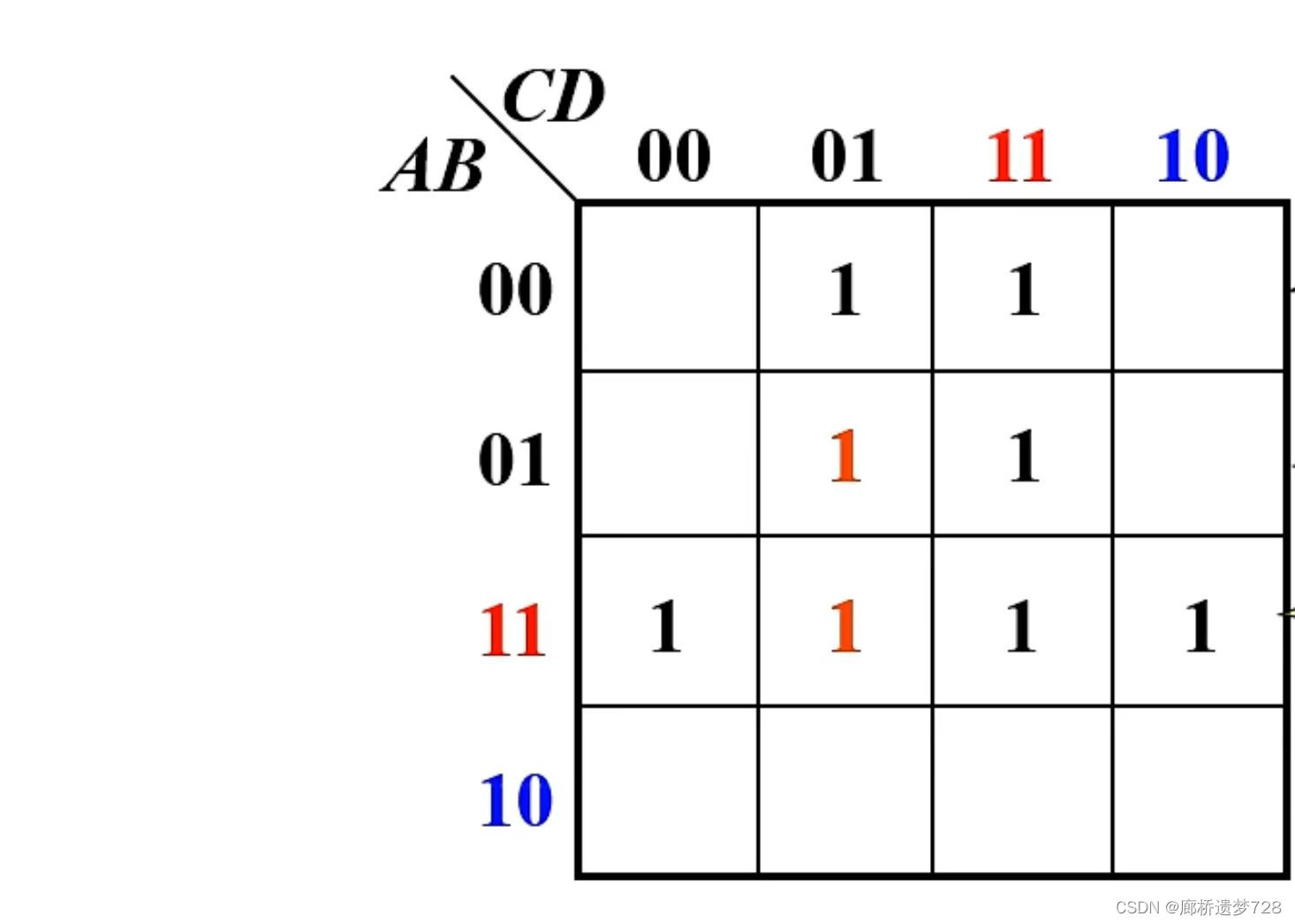
 对非标准与或式：找到交集，满足交集的部分全部填 “1”。例如Y=AB+A'D+BC'D,当AB=1时，即A=1,B=1，找到满足A=1,B=1的全部格子，填上“1”。对于后两项A'D,BC'D同样方法。对应卡诺图如下所示：

 

•  用卡诺图化简逻辑函数

化简依据：用卡诺图化简逻辑函数式，其原理是利用卡诺图的相邻性，对相邻最小项进行合并，消去互反变量，达到化简的目的。

化简规律：

（1）填写卡诺图

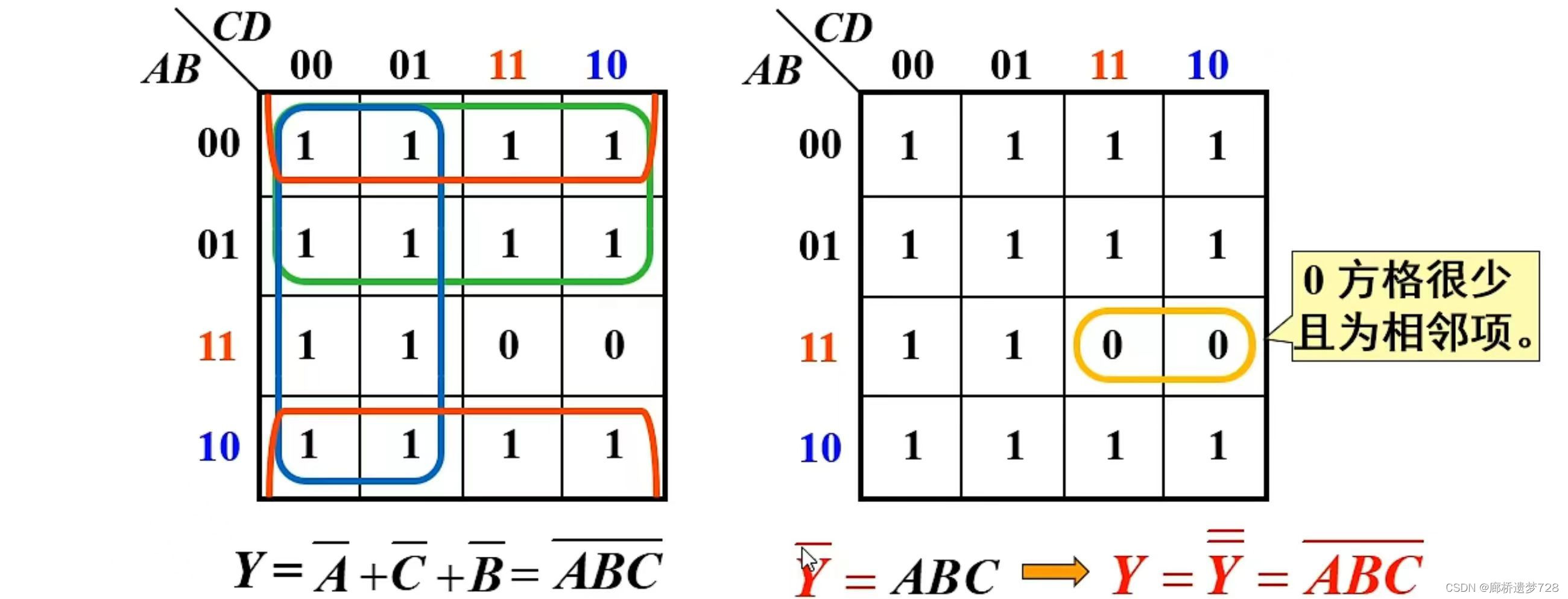
（2）画卡诺圈，将相邻相对的“1”得方格按2^n（1、2、4、……）个 圈为一组，直到所有“1”被圈完；圈越大，消去的变量越多，与项越简单，能画入大圈就不画入小圈；圈数越少越好，化简后的与项就越少；一个最小项可以重复使用，即只要需要，一个方格可以同时被多圈所圈；一个圈中的小方格至少有一个小方格不为其它圈所圈；

（3）将各卡诺图分别化简（找到变量在圈中对应的全部逻辑值，若逻辑值一直不变，则保留；反之则消去。一直为0则为反变量形式、为1则为原变量形式。），然后相加（相或）；

特殊情况：当0方格（空格）很少的时候，可使用圈 “0” 来求出原函数的反函数，再来求原函数的方法。

例如：