离散数学·图的着色

call me by ur name

已于 2023-02-14 12:01:16 修改

阅读量2.8k

点赞数 5

文章标签：矩阵

于 2022-11-21 09:39:09 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_61786525/article/details/127777103

版权

着色

在这里插入图片描述

色数

在这里插入图片描述

k -着色 —— 用k个颜色上色的
色数 —— 最少需要的颜色数
k -色图 —— 最少需要的色的图
χ(……) —— 相应色数

在这里插入图片描述

性质

χ(G)点色数=1 —— 为零图 全是孤立点
χ(K_n)=n
χ(G)=2 —— G为非零图二部图 二部图：一个图的点集可以分为2个互不相交的点集A,B的并，并且在G中的每一条边的2个端点，其中一个在A，另一个在B。

G可2 -着色 —— G是二部图 —— G中无奇圈

χ(G)的上界、Brooks定理

在这里插入图片描述

色多项式

在这里插入图片描述

例

在这里插入图片描述

边着色、Vizing定理

在这里插入图片描述

例

在这里插入图片描述

当然，这道题出现在边着色下方，所以用到边着色的建模，但是实际上自己想的话挺难想到的🥠🥠🥠

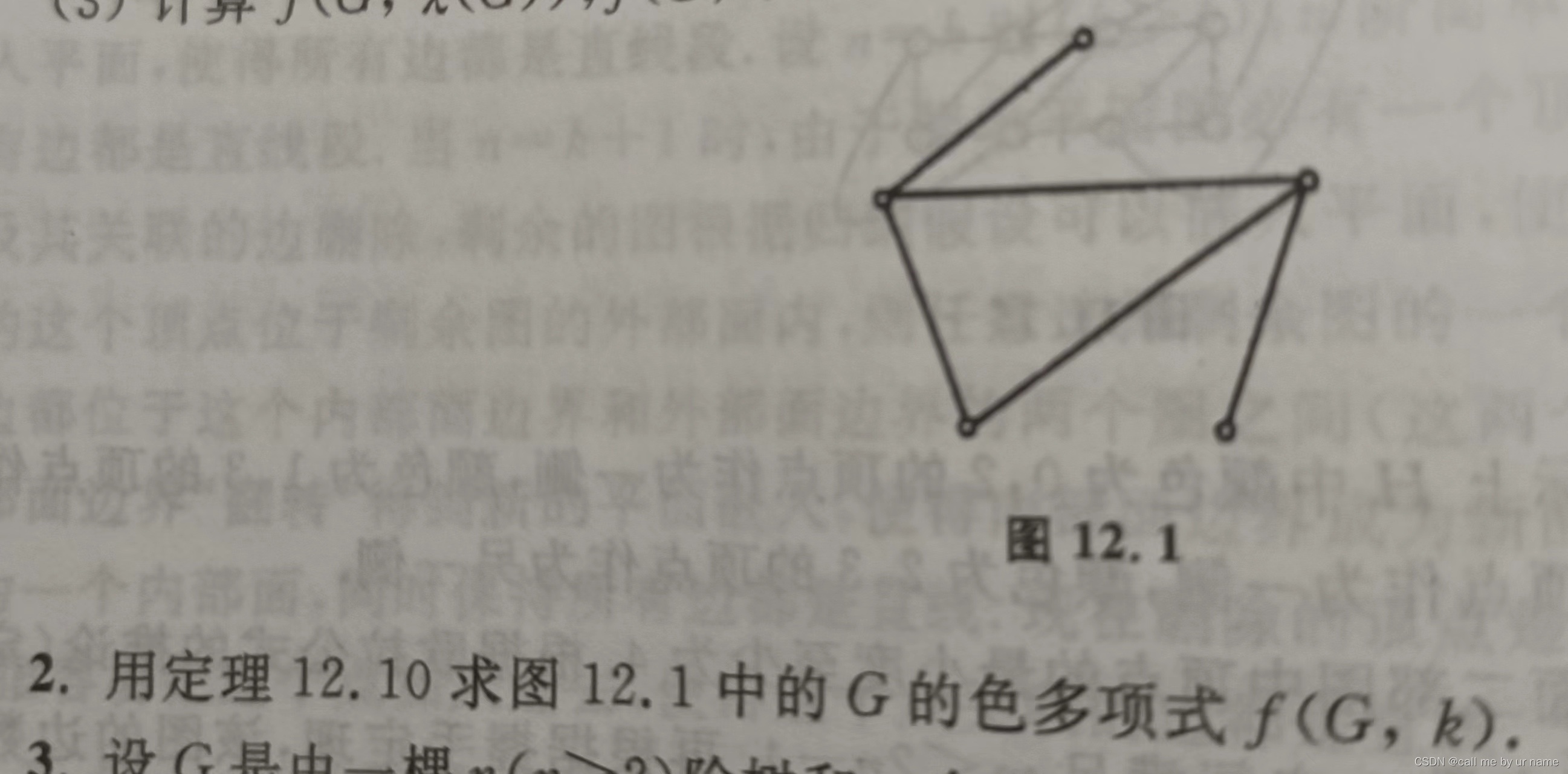
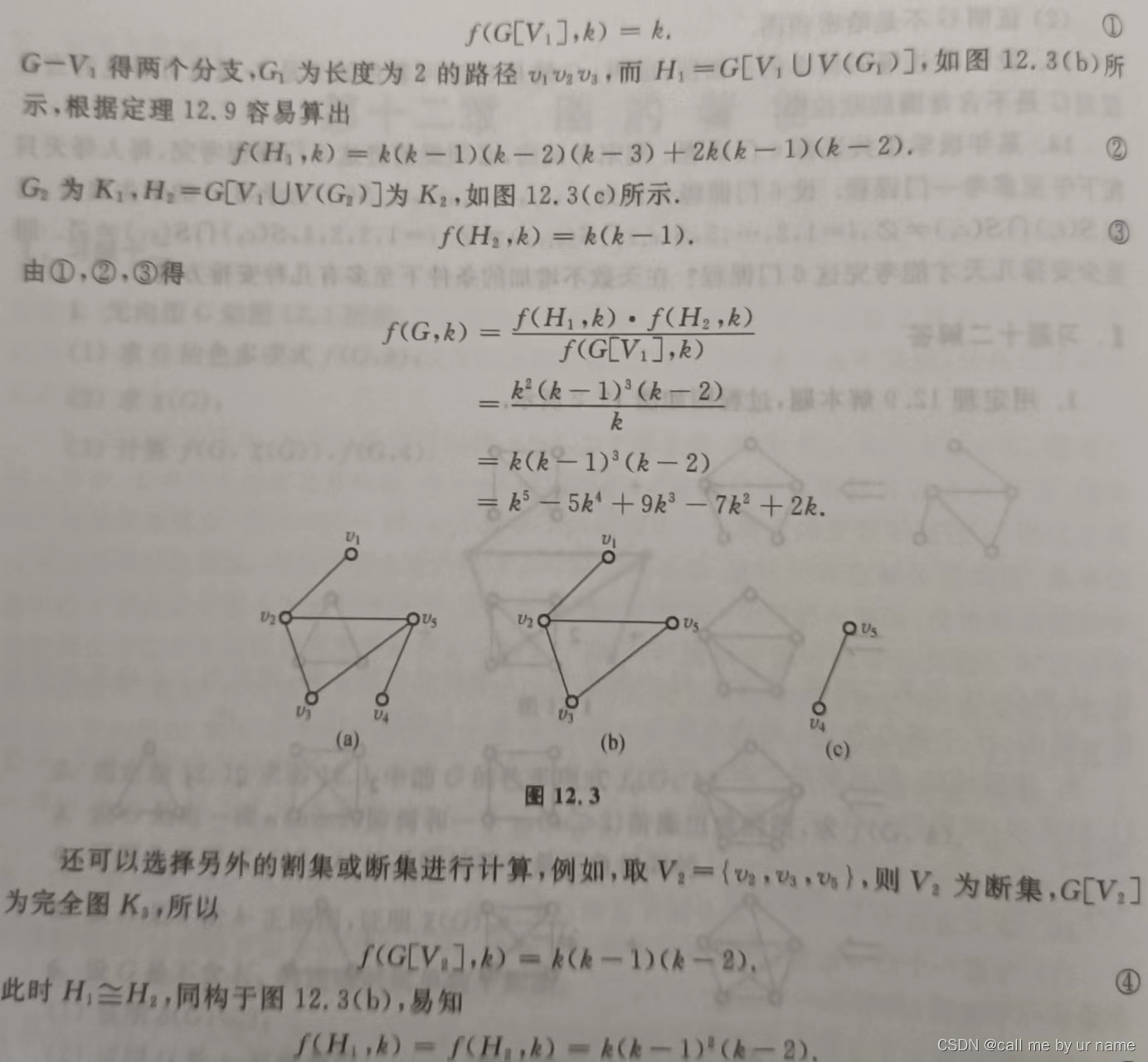
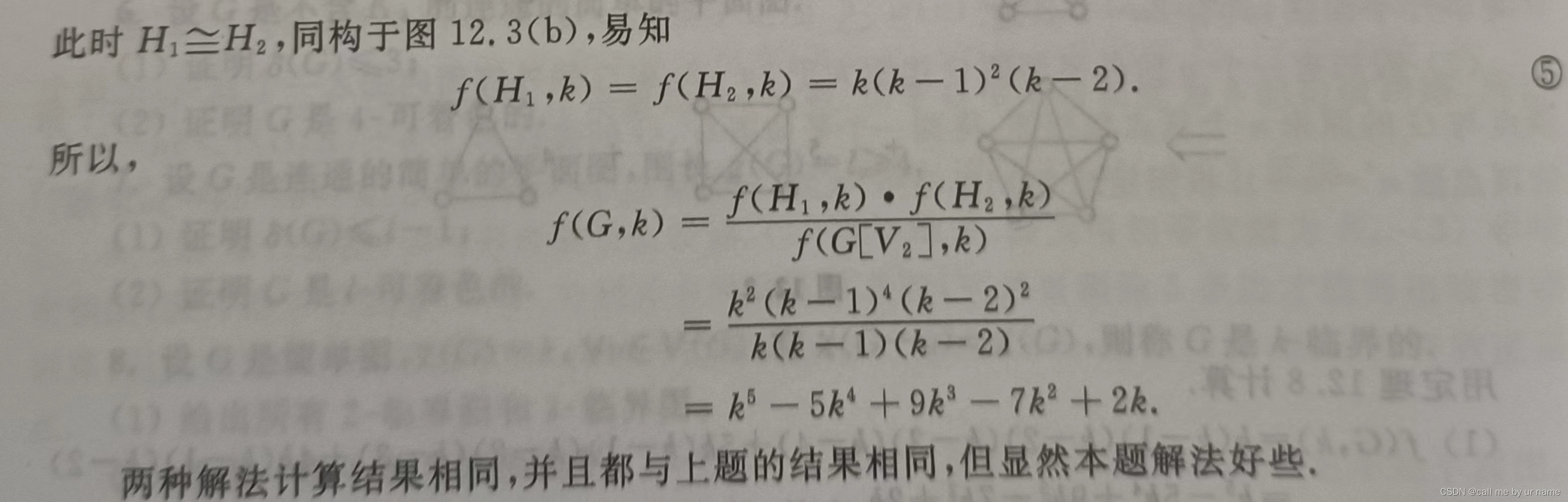
在这里插入图片描述

练习

求色多项式

在这里插入图片描述

有点看不懂，尽量看看吧，实在不会也无所谓了

第3题

在这里插入图片描述

这题不难，但是主要是当2个图组合在一起时，用乘法缔结起来
递推公式用加法

8题

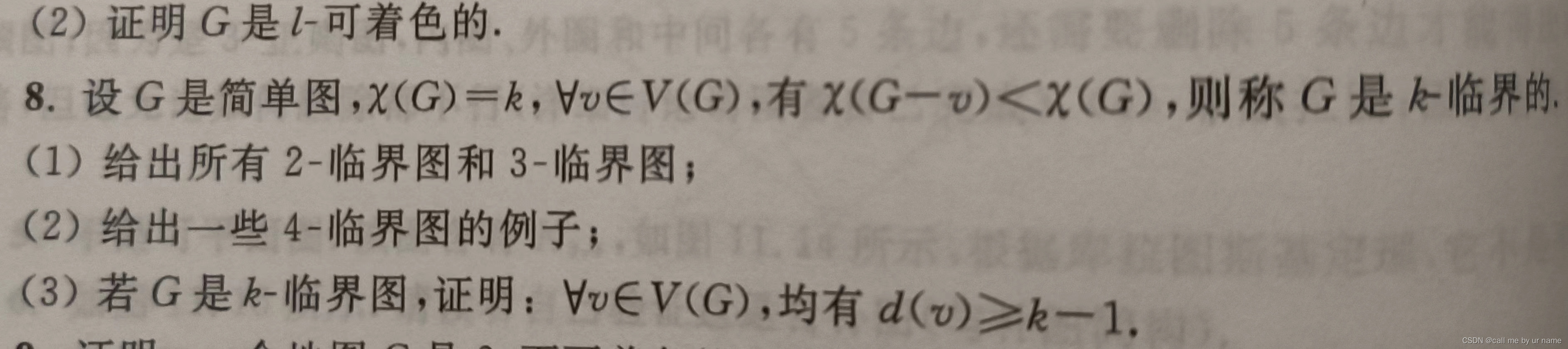
在这里插入图片描述

前2问
看看就行了，有点概念即可，不必强求了

证明题

在这里插入图片描述

看看就行

14

在这里插入图片描述

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。