离散数学平面图对偶图和着色问题

离散数学复习命题公式的范式

离散数学平面图对偶图和着色问题

离散数学谓词逻辑

离散数学-图的运算与基本概念、导出子图、路与连通

离散数学关系的基本运算和关系的性质闭包

离散数学-欧拉图和哈密顿图

平面图定义

交叉点和交叉边：


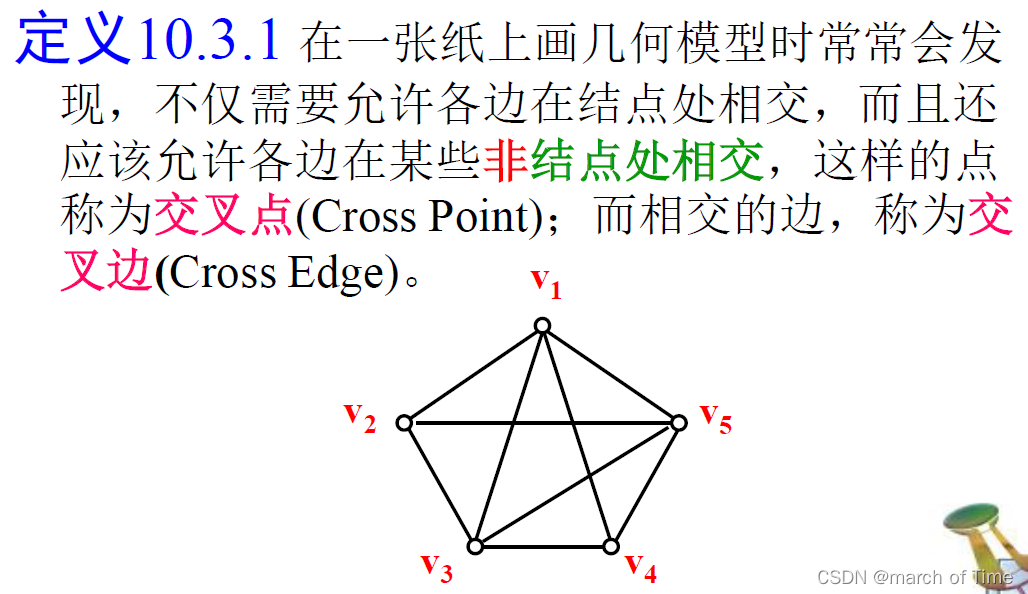
有些图形不论如何改画，除去结点外，总有边相交叉。
即不管怎样改画，至少有一条边与其他边相交叉，故它是非平面图。
平面图可应用到地下管网,电子线路等方面。

平面图的判定

1.观察法

2.欧拉公式判定

在平面图G的一个平面表示中，由边所包围的其内部不包含图(其它结点和边)的结点和边的区域，称为G的一个面(Surface)。
包围该面的诸边所构成的回路称为这个面的边界 (Bound) 。
面r的边界的长度称为该面的次数(Degree)，记为D®。
区域面积有限的面称为有限面(Finite Surface)，区域面积无限的面称为无限面(Infinite Surface)。
平面图有且仅有一个无限面。

定理10.3.1：平面图中所有面的次数之和等于边数的二倍。
证明：
任何一条边，或者是两个面边界的公共边，或者是在一个面中作为边界被重复计算两次，故平面图所有面的次数之和等于其边数的二倍。
1750年，欧拉发现，任何一个凸多面体，若有n个顶点、m条棱和r个面，则有n-m+r = 2。这个公式可以推广到平面图上来，称之为欧拉公式

定理10.3.2：设G = <V, E>是连通平面图，若它有n个结点、m条边和r个面，则有：n-m+r=2 (存在自回路也适用）
证明： 对G的边数m进行归纳。
若m = 0，由于G是连通图，故必有n = 1，这时只有一个无限面，即r = 1。所以n-m+r = 1-0+1 = 2
定理成立。
若m=1，此时有两种情况：
该边是自回路，则有n=1，r=2，这时
n-m+r=1-1+2=2
该边不是自回路，则有n=2，r=1，这时
n-m+r=2-1+1=2
所以m=1时，定理也成立。
 假设对少于m条边的所有连通平面图，欧拉公式
成立。现考虑m条边的连通平面图，设它有n个
结点。分以下两种情况：
m条边的情况：
若G是树，那么m=n-1，这时r=1。所以
n-m+r=n-(n-1)+1=2
若G不是树，则G中必有回路，因此有基本回路，设e是某基本回路的一条边，则G’=<V,E-{e}>仍是连通平面图，它有n个结点，m-1条边和r-1个面，按归纳假设知：n-(m-1)+(r-1)=2
整理得：n-m+r=2
所以对m条边时，欧拉公式也成立。

定理10.3.2推论：设G是一个(n,m)简单连通平面图，
若m＞1，则有:m≤3n-6（注意是简单连通平面图，简单图没有自回路和平行边）

不等式m≤3n-6是判断一个简单连通图是平面图的必要非充分条件。
满足不等式的简单连通图未必是平面图。
但该推论的逆否命题却非常有用，可以用它来判定某些图是非平面图。
例子：证明完全图K5是非平面图

定理：设G为一平面连通简单图，其结点数n≥4,边数为m，且G不以K3为其子图，则有m≤2n-4。
证明：由于G是不以K3为子图的简单图，故G中每个面的边界长度不小于4。而G的k个面的边界长度和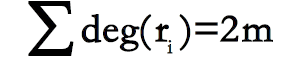
，所以2m ≥4k，再结合欧拉公式n-m+k=2, 则有m≤2n-4。

例子：不使用观察法证明图K3,3是一个非平面图。

证明： 事实上，假设K3,3是一个平面图，那么它的每个面的次数均不能小于等于3，即每个面的次数均大于等于k(k≥4)，
m=9, 2n-4=12-4=8, 有m ≥ 2n-4，结合上页定理，所以K3,3一定不是平面图

3.库拉托夫斯基定理

对于任意给定的图G=<V,E>:
设e=(u,v)是G的任意一条边，如果在图G中删除该边并新增一个结点w及两条边e1=(u,w)，e2=(w,v)，则称该操作为对图G边切割操作；
设w是G中任意一个度数为2的结点，且是边e1=(u,w)和e2=(w,v)的公共结点，如果在图G中删除结点w及边e1和e2，并增加边e1=(u,v),则称该操作为对图G的结点贯通操作；
对图G的边切割操作和结点贯通操作统称为对图G的同胚操作。
定理10.3.4(库拉托夫斯基定理)，
一个图是平面图的充分必要条件是它的任何子图都不同胚于K5或K3,3。（任意一个图判断是否是平面图的充要条件）
定理10.3.4(库拉托夫斯基定理) 一个图是平面图的充分必要条件是它的任何子图都不可能收缩为K5或K3,3。
定理10.3.3推论 一个图是非平面图的充分必要条件是它存在一个能收缩为K5或K3,3的子图。
K5和K3,3被称为库拉托夫斯基图。

对偶图

对偶图的概念


对偶图的结论：

着色问题

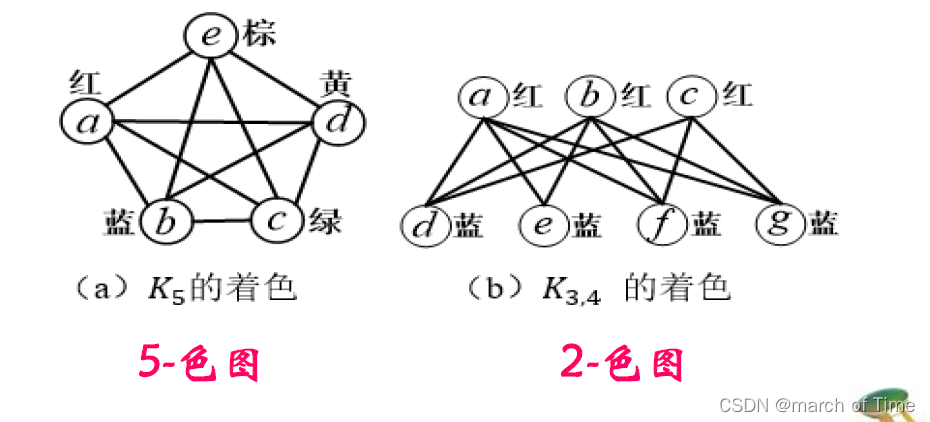
着色图的性质

布鲁克斯定理 维津定理

应用：


边着色

维津定理

面着色

面着色可以转化为点着色来完成。
定理：地图G是k-面可色的，当且仅当它的对偶图G*是k-可色图。
定理：若图G是一个简单平面图，则该图中至少存在一个度数小于或等于5的结点。
五色定理：设G=<V,E>是任意给定的一个连通简单平面图，则G的点色数为5。
四色猜想：连通简单平面图的色数不超过4。