洛谷B3637 最长上升子序列|线性DP、模板题

题目：

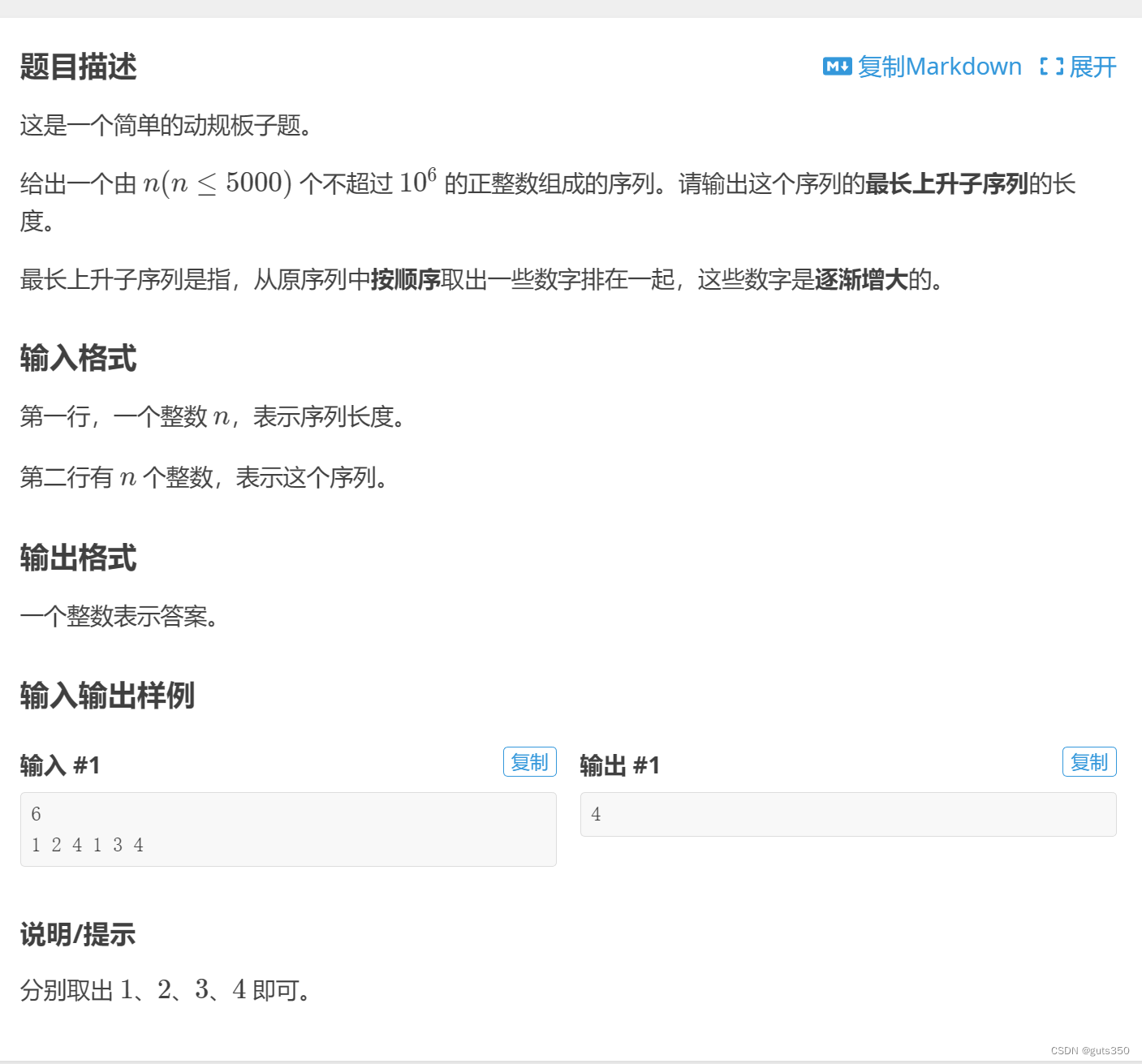
B3637 最长上升子序列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

 注意点：

学习：https://blog.csdn.net/weixin_72060925/article/details/128425930

虽然这道题已经见过很多类似的变形了，但是还是犯迷糊。

1.首先，没有初始化每个dp元素，误以为总有一个    dp[i]=max(dp[i],dp[j]+1);会把当前的dp赋值为1，然而如果前面的数都大于这个数，这个dp依旧是0，所以需要手动初始化为1。

2.忘记了还要在每个dp元素里再找一个最大的。因为不确定最长递增子序列以哪个元素结尾，但是一定以某个元素结尾，求出了以每个元素结尾的最长长度，答案在里面选即可。

3.还考虑r[i]表示数列里出现的数字i对应的最大长度，配合上dp[i]表示以i结尾的最长长度（那么dp[i]就等于r[小于a[i]的所有数]中的最大长度+1），但是数的范围达到了1e6，满足递增的话，还是要一个一个从a[i]-1去遍历到0，时间复杂度太高，不行。类似蓝桥杯的接龙序列，只有10个情况比较适合这样做，而且那道题因为是头尾相同可以直接找到，不用一一遍历。

蓝桥杯23年第十四届省赛-接龙数列|DFS、线性DP-CSDN博客

再总结一下类似的套路：

对于子序列问题，可以构造一个dp[i]数组，表示以第i个元素结尾的目标值（如最长长度），如果是连续的子序列，从dp[i-1]递推来就可以；如果子序列不要求连续元素，那么就要从前i-1项dp递推来，比较出目标值。最后，在所有的dp中挑出一个值作为答案。

 

代码：

#include <bits/stdc++.h>

using namespace std;
const int N=1e6+10;
const int M=5e3+10;
//以某个数字结尾的最长子序列
int dp[M],r[N];

int a[M];
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	int n;
	cin>>n;
	
	for(int i=0;i<n;++i){
		cin>>a[i];
	}
    int ans=0;
    dp[0]=1;
    
    for(int i=1;i<n;++i){
    	//要初始化为1，因为可能存在前面都比它大的情况 ，就不会进入下面的dp赋值的语句 
        dp[i]=1;
    	for(int j=i-1;j>=0;j--){
    		if(a[j]<a[i]){
    			dp[i]=max(dp[i],dp[j]+1);
			}
		}
		
		//还需要在所有以第i个数为结尾的 最长长度里选一个最长的 
		if(dp[i]>ans) ans=dp[i];
	}

   cout<<ans;
   return 0;
}

注意点第3点考虑的方法，r[i]表示数列里出现的数字i对应的最大长度：

#include <bits/stdc++.h>

using namespace std;
const int N=1e6+10;
const int M=5e3+10;
//以某个数字结尾的最长子序列
int dp[M],r[N];

int a[M];
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	int n;
	cin>>n;
	
	for(int i=0;i<n;++i){
		cin>>a[i];
	}
    int ans=0;
    dp[0]=1;r[a[0]]=1; 
    
//    for(int i=1;i<n;++i){
//    	//要初始化为1，因为可能存在前面都比它大的情况 ，就不会进入下面的dp赋值的语句 
//        dp[i]=1;
//    	for(int j=i-1;j>=0;j--){
//    		if(a[j]<a[i]){
//    			dp[i]=max(dp[i],dp[j]+1);
//			}
//		}
//		
//		//还需要在所有以第i个数为结尾的 最长长度里选一个最长的 
//		if(dp[i]>ans) ans=dp[i];
//	}

    for(int i=1;i<n;++i){
    	//要初始化为1，因为可能存在前面都比它大的情况 ，就不会进入下面的dp赋值的语句 
        dp[i]=1;
    	for(int j=a[i]-1;j>=0;j--){
    		dp[i]=max(r[j]+1,dp[i]);
		}
		
		r[a[i]]=max(r[a[i]],dp[i]);
		//还需要在所有以第i个数为结尾的 最长长度里选一个最长的 
		if(dp[i]>ans) ans=dp[i];
	}
	
	
   cout<<ans;
   return 0;
}