【数据结构与算法分析】0基础带你学数据结构与算法分析11--AVL树

目录

二分查找

AVL 树

AVL 的平衡因子

AVL 的插入操作

单旋转

双旋转

对 AVL 树插入的总结

AVL 的移除操作

---

如果给定一个序列，你将如何在这个序列中查找一个给定元素 target，当找到时返回该元素的迭代器，否则返回末尾迭代器。首先排除时间复杂度 O(N) 的朴素算法，这不是本文的重点。

二分查找

二分法 (Dichotomy) 是一种思想，将一个整体事物分割成两部分，这两部分必须是互补事件，即所有事物必须属于双方中的一方且互斥。如此我们就可以在 O(1) 的时间内将问题大小减半。

二分查找 (binary search)，又称折半查找，这是一种可以在 O(log⁡N)时间复杂度下完成查找的算法。二分查找要求序列必须是有序的，才能正确执行：将序列划分为两部分，如果中间值大于 target，意味着这之后的值都大于 target，需要继续向前找；如果中间值小于 target，意味着这之前的所有值都小于 target，需要继续向后找。

AVL 树

上一篇介绍树时分析了 BST 中为什么很容易发生不平衡现象。在极端情况下，只有一个 leaf 的树，在查找元素时其时间复杂度退化为 O(N) 。

为了防止 BST 退化为链表，必须保证其可以维持树的平衡，一次需要有一个 平衡条件 (balanced condition)。如果每个结点都要求其左右子树具有相同的高度，显然是不可能的，因为这样实在是太难了。在 1962 年，由苏联计算机科学家 G.M.Adelson-Velsky 和 Evgenii Landis 在其论文 An algorithm for the organization of information 中公开了数据结构 AVL (Adelson-Velsky and Landis) 树，这是计算机科学中 最早被发现的 自平衡二叉树。

AVL 的平衡因子

AVL 树将子树的高度限制在差为 1，即一个结点，如果其左子树与由子树的高度差 ∣Dh∣≤1 ，则认为这棵树是平衡的。因此带有平衡因子 -1、 0 或 1 的结点被认为是平衡的，而 -2 或 2 的平衡因子被认为是需要调整的。平衡因子可以直接存储于结点之中，也可以利用存储在结点中的子树高度计算得出。

 简单地计算，一棵 AVL 树的高度最多为 1.44log⁡(N+2)−1.328，实际上的高度只比 log⁡N 稍微多一些。一棵高度为 h 的 AVL 树，其最少结点数 S(h) = S(h - 1) + S(h - 2) + 1 ，S(0)=1, S(1) = 2 。而 AVL 的所有操作均可以在 O(log⁡N) 复杂度下完成。

AVL 的插入操作

在进行插入操作时，和普通的 BST 类似，但是不一样的是需要更新路径上所有结点的平衡信息，并插入完成后有可能破坏 AVL 的特性。如果特性被破坏后，需要恢复平衡才能算插入结束。实际上，总可以通过简单的操作进行修正，这种操作被称为 旋转 (rotation)。

将必须重新平衡的结点叫作 α ，由于任意结点最多有两个孩子，因此高度不平衡时， α 点的两棵子树的高度差 2。这种不平衡可能出现在下面 4 中情况中：

1. 对 α 的左孩子的左子树进行插入
2. 对 α 的左孩子的右子树进行插入
3. 对 α 的右孩子的左子树进行插入
4. 对 α 的右孩子的右子树进行插入

情况 1 和 4 关于结点 α 镜像对称，情况 2 和 3 关于结点 α 镜像对称。因此从逻辑上来讲，我们只需要考虑两种情况，而编程时需要考虑上面介绍到的所有 4 种情况。

单旋转

情况 1 是插入发生在「外边」的情形，我们称之为 一字形 (zig-zig)，可以用 单旋转 (single rotation) 解决。假设结点 n 不满足 AVL 平衡性质，因为其左子树比右子树深 2 层，可以对其进行单旋转修正。修正的过程是：将左子树的根 l 向上移动一层，而将 n 向下移动一层， n 作为 l 的孩子出现在树中。下图展示了插入后出现不平衡的结点 (红色) 、如何旋转、多余子树如何处理以及子树的层数 (蓝字)。

 

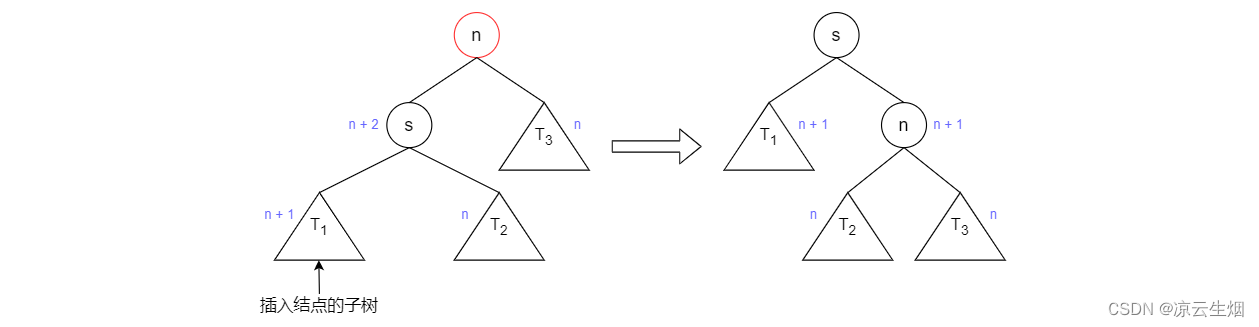
对应的情况 4 也是 zig-zig，只需要旋转的方向与操作相镜像即可处理。

双旋转

对于情况 2 、 3 来说，插入在「树内」从而导致 AVL 树无效，这种情况被称为 之字形 (zig-zag)，而子树太深通过 single rotation 无法让树平衡，解决这种内部的情形需要 双旋转(double rotation) 解决。

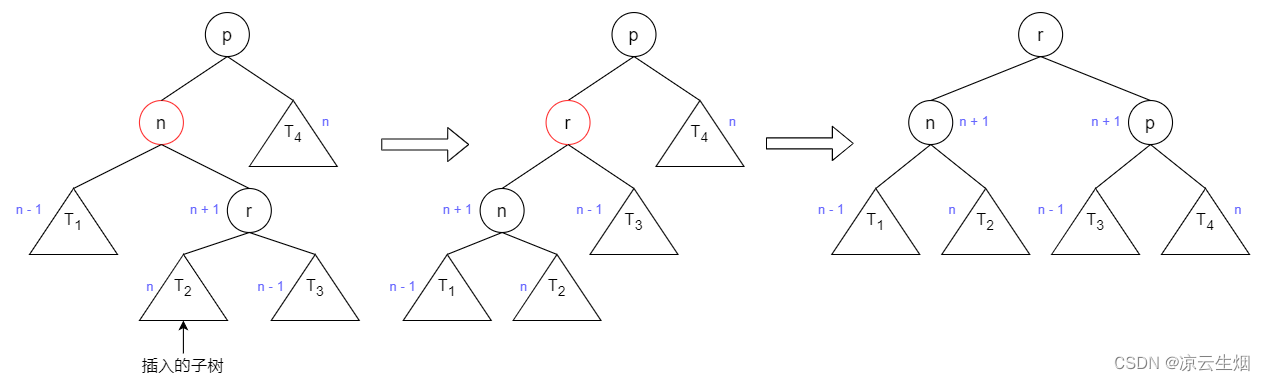
 对应的情况 3 也是 zig-zag，只需要旋转的方向与操作相镜像即可处理。

对 AVL 树插入的总结

可以发现，无论单旋转与双旋转，它都由两个最基本的操作组成：将结点进行左旋 (left rotation) 或右旋 (right rotation)，并将多余的一棵子树挂载到下降结点上。

// 左旋
void rotate_left(Node* node) {
  Node* child = node->right;
  node->right = child->left;
  if (child->left != nullptr) {
    child->left->parent = node;
  }
  child->parent = node->parent;
  child->left = node;
  node->parent = child;
  return child;
}
// 右旋
void rotate_right(Node* node) {
  Node* child = node->left;
  node->left = child->right;
  if (child->right != nullptr) {
    child->right->parent = node;
  }
  child->parent = node->parent;
  child->right = node;
  node->parent = child;
  return child;
}

在进行编程时，可以首先定义左右旋这两种基本操作，在根据情况判断如何组合。对于编程细节，远比理论多得多，编写正确的 loop 算法相对于 recursion 并不是一件容易的事，因此更多的会使用 recursion 进行实现。

还有一个重要问题是如何高效的对高度信息进行存储，可以采用平衡因子作为存储而不是一个 int 类型的高度，或者更近一步，利用 2 bit 存储平衡因子 (毕竟只有 3 个状态)。如果你希望将其隐藏到指针中，也是个不错的选择。存储平衡因子将得到些许速度优势，但丧失了简明性，如果你使用隐藏于指针的方法，更加剧的这一问题，不过好消息是你能为此剩下不少内存空间。

AVL 的移除操作

AVL 树的移除与 BST 相当，同样地，移除操作可能会破坏 AVL 特性，因此我们在移除元素后，同样需要对树进行平衡才能算操作完成。