使用SPSS进行时间序列分析

数据

Date		Value	
09/12/16	1324.60
10/03/16	1313.30
11/01/16	1288.45
12/01/16	1161.85
01/03/17	1151.00
02/01/17	1203.65
03/01/17	1240.40
04/03/17	1247.25
05/02/17	1255.45
06/01/17	1264.85
07/03/17	1229.25
08/01/17	1270.95
09/01/17	1320.40
10/02/17	1273.70
11/01/17	1277.05
12/01/17	1275.50
01/02/18	1312.05
02/01/18	1341.35
03/01/18	1307.75
04/03/18	1333.45
05/01/18	1307.10
06/01/18	1294.60
07/02/18	1247.80
08/01/18	1219.00
09/03/18	1200.05
10/01/18	1189.35
11/01/18	1231.15
12/03/18	1230.30
01/02/19	1282.90
02/01/19	1318.70
03/01/19	1311.95
04/01/19	1293.50
05/01/19	1283.80
06/03/19	1317.10
07/01/19	1390.10
08/01/19	1406.80
09/02/19	1525.95
10/01/19	1473.45
11/01/19	1508.80
12/02/19	1461.15
01/02/20	1527.10
02/03/20	1574.75
03/02/20	1599.65
04/01/20	1576.55
05/01/20	1686.25
06/01/20	1730.60
07/01/20	1771.05
08/03/20	1958.55
09/01/20	1972.35
10/01/20	1902.00
11/02/20	1889.90
12/01/20	1810.75
01/04/21	1943.20
02/01/21	1862.95
03/01/21	1734.15
04/01/21	1726.05
05/04/21	1797.75
06/01/21	1899.35
07/01/21	1781.50
08/02/21	1811.45
09/10/21	1794.60

步骤

1、定义日期标示变量：即先将序列的时间定义好，才能分析其时间特征。

2、了解序列发展趋势：即序列图，确定乘性还是加性。

如何根据序列图来判断模型的乘性或加性？

如果随着时间的推移，序列的季节波动变得越来越大，则建议使用乘法模型。如果序列的季节波动能够基本维持恒定，则建议使用加法模型。

3、进行季节因素分解。

**ERR（误差序列）：**从时间序列中移除季节因素、长期趋势、和循环变动之后留下的序列，也就是原始序列中的不规则变动构成的序列。
**SAS（季节因素校正后序列）：**是移除原始序列中的季节因素后的校正序列。
**SAF（季节因子）：**是从序列中分解出的季节因素。其中的变量值根据季节周期的变动进行重复，如本例中季节周期为12个月，所以这些季节因子没12个月重复一次。
**STC（长期趋势和循环变动趋势）：**这是原始序列中长期趋势和循环变动构成的序列。

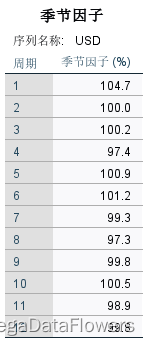
周期为12个月，季节因子12个月循环一次。

完成季节因素分解后的序列和原始序列之间有什么差异？

通过回执序列图的方法把原始序列和除去季节因子的三个序列（误差序列、季节因素校正后序列、长期无视和循环变动序列）进行比较。


做四个序列图，会有四个变量：

1 原始序列：使用变量USD
2 误差序列：使用变量ERR
3 季节因素校场后序列：使用变量SAS
4 长期趋势和循环变动序列：使用变量STC

因为误差序列数值非常小，所以长期趋势和循环变动序列（长期趋势+循环变动）与季节因素校正后序列（长期趋势+循环变动+不规则变动，即误差）能够基本重合。

在单独做 季节因子SAF 的序列图：


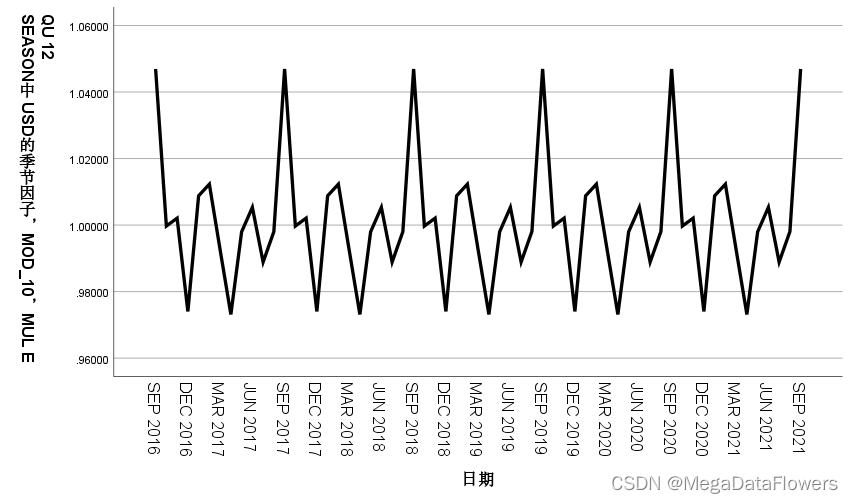
通过对原始序列的季节分解，我们更好的掌握了原始序列所包含的时间特征，从而选用适当的模型进行预测。

4、建模





5、分析结果解读

该表主要通过 R方 或 平稳R方 来评估模型拟合度，以及在多个模型时，通过比较统计量找到最优模型。


6、预测


未来一年是到2022年12月，手动输入即可。


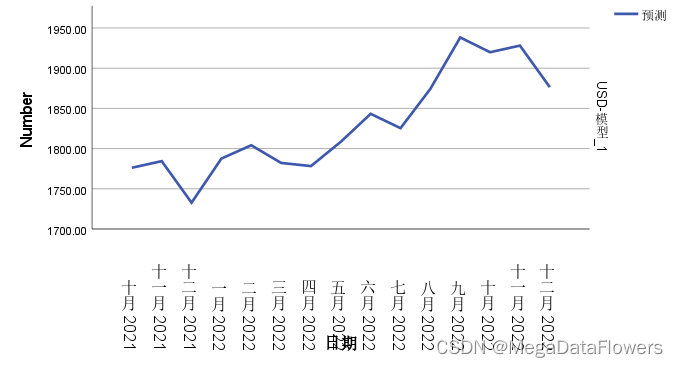
这是未来一年的趋势。

如果想从全局来观察预测趋势，可以在把这一年的趋势和以前的数据连接起来。

原始的 和 2022年预测的