可视化B树详细代码实现

已于 2023-09-01 23:10:09 修改
阅读量320 收藏 6
点赞数
分类专栏： 数据结构 文章标签： b树 前端框架 数据结构 c++
于 2023-08-08 14:38:16 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_62617798/article/details/132118496
版权

文章目录


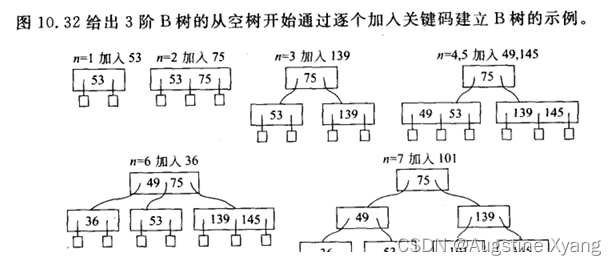
本次实验将实现一棵具备完整功能且正常运行的B树，并用dot脚本语言实现B树的可视化，能够根据操作实时进行B树的结构变换。

参考教材：殷人昆老师版 数据结构

代码链接：BTree Visualize

数据结构：B树

此处仅做简介，详细请见教材。B树是一种常用的多路平衡搜索树（也称为多叉树），可以看作平衡二叉树的更为平常的版本，但是拥有m路的B树更加复杂。B树被广泛应用于数据库和文件系统等存储结构中，以支持高效的数据插入、删除和查找操作。B树的特点是每个节点可以存储多个关键码（即key值），并且节点之间的高度尽量保持一致，从根节点到每一个叶子节点的路径长度基本相等，且失败节点均在同一层上，保证了数据的均衡性和快速访问。

在这里插入图片描述

B树有如下特性：

  1. 每个节点最多有M个子节点（M>=2），即最多有M-1个关键码。通常情况下，M的值很大，可以存储大量的关键字，从而减少树的高度，提高数据访问效率；
  2. 根节点至少有两个子节点；
  3. 非根节点至少有ceil(M/2)个子节点，即至少有(M-1)/2个关键码；
  4. 所有叶子节点位于同一层，即它们具有相同的深度；
  5. B树的插入和删除操作都需要进行树的平衡调整，以保持B树的特性。
    在插入操作中，如果插入后导致节点的关键字数超过了M-1个，需要进行节点的分裂，将一部分关键字移到一个新节点中，然后将新节点插入到父节点中。
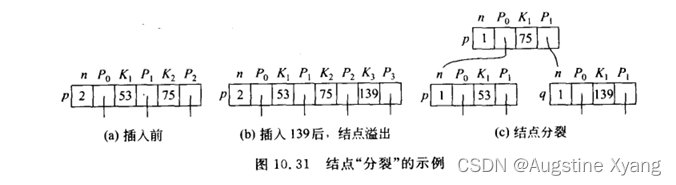
    在这里插入图片描述
    在这里插入图片描述

在删除操作中，如果删除导致节点的关键字数少于(M-1)/2个，需要进行节点的合并，将相邻的两个节点合并为一个节点，然后将父节点中的关键字删除。
在这里插入图片描述

B树的平衡调整过程比较复杂，但它保证了B树各路的高度平衡，从而保证了高效的数据访问速度。B树的应用广泛，特别是在数据库索引和文件系统中，它能够高效地支持大规模数据的存储和查询。

B树代码实现

查找

这是B树的基本功能，search方法会根据关键码在树中搜寻其位置，如果搜寻不到，则会返回该关键码的插入位置

struct ans
{
	Bnode* r;   //地址
	int i;    //关键码
	bool tag;  // 0成功，1失败
};

ans BTree::search(const int& x)
{
	ans result;
	Bnode* p = root, * q = NULL;//p为扫描指针，q为p的父结点指针
	int i = 0;
	while (p != NULL)
	{
		i = 0;
		p->key[(p->num) + 1] = maxValue;
		while (p->key[i + 1] < x)i++;
		if (p->key[i + 1] == x)
		{
			result.r = p;
			result.i = i + 1;
			result.tag = 0;
			return result;
		}
		q = p;
		p = p->child[i];    //下移到相应子树

	}
	result.r = q;
	result.i = i;   //记录位置i
	result.tag = 1;
	return result;
}

插入

插入操作会先调用search方法，即可找到该关键码在树中应当插入的位置



bool BTree::insertKey(Bnode* p, const int& x, Bnode* rp)  //用于在p节点中插入一项x
{
	int i = p->num;
	while (i > 0 && x < p->key[i])
	{
		p->key[i + 1] = p->key[i];//向后移位
		p->child[i + 1] = p->child[i];
		i--;
	}


	p->key[i + 1] = x;   //插入x
	p->child[i + 1] = rp;
	p->num++;

	return true;
}


bool BTree::insert(const int& x)
{
	ans pos = search(x);
	if (!pos.tag)
		return false;//x已经存在
	Bnode* p = pos.r;  //p为要插入的地址
	Bnode* q, * t, * rp = NULL;
	int k = x;
	int j = pos.i;

	while (true)
	{
		if (p->num < m - 1)   //关键码个数未超出
		{
			insertKey(p, k, rp);
			return true;
		}
		int s = (m + 1) / 2;     //溢出则分裂结点,s为中间项
		insertKey(p, k, rp);          //先插入x
		q = new Bnode(m);           //分裂结点，先建立新结点
		move(p, q, s, m);          //将p的key[s+1...m]和child[s...m]移动到q的key[1...m-s]和child[0...m-s]，p.n变为s-1，q.n变为m-s
		k = p->key[s];             //新要插入的结点，p中只剩下s-1个关键码，p中有m-s个关键码
		p->key[s] = maxValue;
		rp = q;                    //形成新的插入二元组（k,rp）
		if (p->parent != NULL)
		{
			t = p->parent;
			t->key[(t->num) + 1] = maxValue;
			q->parent = p->parent;
			p = t;
		}
		else
		{
			root = new Bnode(m);
			root->num = 1;
			root->parent = NULL;
			root->key[1] = k;
			root->child[0] = p;
			root->child[1] = rp;
			q->parent = p->parent = root;
			return true;
		}

	}


}

当结点关键码超出限制时，会进行结点的分裂，此时用到了move()函数，用于将p的key[s+1…m]和child[s…m]移动到q的key[1…m-s]和child[0…m-s]，p.n变为s-1，q.n变为m-s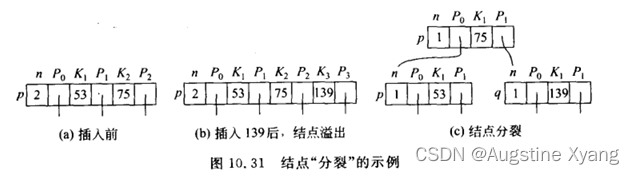在这里插入图片描述

void BTree::move(Bnode* p, Bnode* q, int s, int m)//将p的key[s+1...m]和child[s...m]移动到q的key[1...m-s]和child[0...m-s]，p.n变为s-1，q.n变为m-s
{
	int i;
	for (i = 1; i <= m - s; i++)
	{
		q->key[i] = p->key[i + s];
		q->child[i - 1] = p->child[i + s - 1];
		if (q->child[i - 1] != NULL)q->child[i - 1]->parent = q;
		p->child[i + s - 1] = NULL;
	}
	q->child[m - s] = p->child[m];
	if (q->child[m - s] != NULL)q->child[m - s]->parent = q;
	p->child[m] = NULL;
	p->num = s - 1;
	q->num = m - s;
}

删除

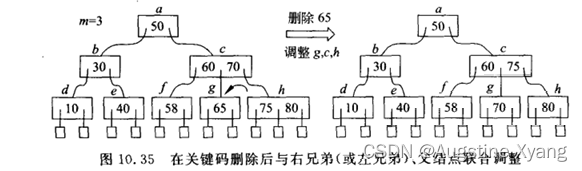
个人认为删除是B树中最为复杂的操作，会涉及结点关键码的左右调整等。

删除时，会先进行search找到想要删除的关键码的位置，如果位于非叶结点，那么先删去该关键码K，再将该结点的子树的最小关键码x来代替K的位置即可，这样可以做到保证B树的性质不变。紧接着，需要在x所在的叶结点中删去x。

综上，B树的删除操作都可以归结为在叶结点中删去关键码的操作，此时有4种情况：

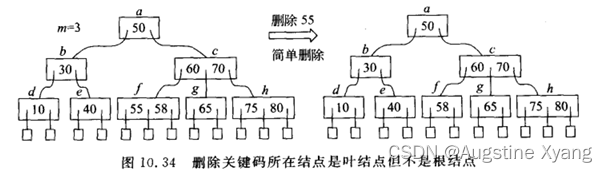
  1. 该叶结点也是根节点，且关键码数num>=2 ，直接删去即可；在这里插入图片描述

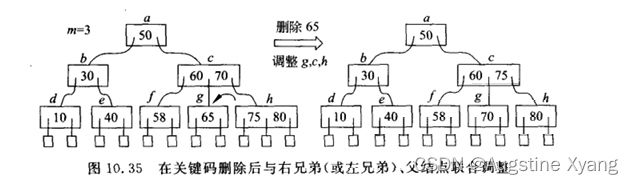
  2. 非根节点，并且关键码数>=ceil(M/2)，也可直接删除在这里插入图片描述

  3. 删除前关键码数=ceil(M/2)-1，且其（左/右）兄弟结点关键码数>=ceil(M/2)，则联合父节点进行关键码的调整，从其兄弟结点中“偷取”关键码来满足B树的结构
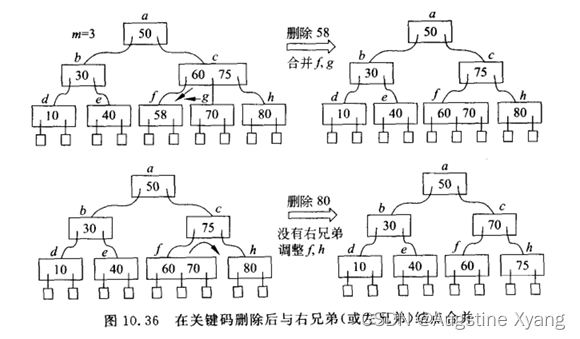
    在这里插入图片描述

  4. 删除前关键码数=ceil(M/2)-1，且其（左/右）兄弟结点关键码数=ceil(M/2)-1，此时需要merge两个结点，形成一个新的结点
    在这里插入图片描述

代码实现为：


bool BTree::remove(const int& x)
{
	ans pos = search(x);
	if (pos.tag == 1)return false;
	Bnode* p = pos.r;
	Bnode* q, * s;
	int j = pos.i;
	if (p->child[j] != NULL)   //非叶节点
	{
		s = p->child[j];
		q = p;
		while (s != NULL)     //寻找叶节点
		{
			q = s;
			s = s->child[0];
		}
		p->key[j] = q->key[1];    //从叶节点找到替补
		compress(q, 1);     //删去叶结点中最小元
		p = q;         //转换为叶结点的删除

	}
	else compress(p, j);
	int d = (m + 1) / 2;
	while (true)
	{
		if (p->num < d - 1)      //关键码数过少
		{
			j = 0;
			q = p->parent;     //开始从父节点中调整
			while (j <= q->num && q->child[j] != p)
			{
				j++;    //
			}
			if (j == q->num)    //p是q的最后个子树，p与q与p的左兄弟进行调整
				rightAdjust(p, q, d, j);
			else               //一般情况下，与q和p的右兄弟进行调整
				leftAdjust(p, q, d, j);
			p = q;          //向上调整
			if (p == root)break;
		}
		else
			break;   //关键码数量足够支持删除
	}
	if (root->num == 0)   //调整后根为0
	{
		p = root->child[0];
		delete root;
		root = p;
		root->parent = NULL;
	}
	return true;

}

其中compress用于删去某结点中第i个关键码：

void BTree::compress(Bnode* p, int pos)
{
	for (int i = pos; i < p->num; i++)
	{
		p->key[i] = p->key[i + 1];
		p->child[i] = p->child[i + 1];
	}
	p->key[p->num] = maxValue;
	p->child[p->num] = NULL;
	p->num--;
}

leftAdjust和rightAdjust用于进行结点关键码的调整：


void BTree::rightAdjust(Bnode* p, Bnode* q, int d, int j)//与左子树调整
{
	Bnode* p1 = q->child[j - 1];    //p的左兄弟
	if (p1->num > d - 1)          //第三种情况，左兄弟关键码足够分给p
	{
		p->num++;
		for (int i = 2; i <= p->num; i++)
		{
			p->key[i] = p->key[i - 1];
			p->child[i] = p->child[i - 1];
		}
		p->key[1] = q->key[j - 1];   //父节点相应关键码下沉
		q->key[j - 1] = p1->key[p1->num];  //左兄弟最大关键码上移
		p->child[0] = p1->child[p1->num];
		p1->child[p1->num] = NULL;
		p1->key[p1->num] = maxValue;
		p1->num--;

	}
	else
		merge(p1, q, p, j); //第四种情况，需要进行合并
}


void BTree::merge(Bnode* p, Bnode* q, Bnode* p1, int j) //结点合并
{
	p->key[(p->num) + 1] = q->key[j];
	p->child[(p->num) + 1] = p1->child[0];
	for (int i = 1; i <= p1->num; i++)
	{
		p->key[p->num + 1 + i] = p1->key[i];
		p->child[p->num + 1 + i] = p1->child[i];
	}
	compress(q, j);   //将父节点进行压缩，j后的key和child左移
	p->num = p->num + p1->num + 1;
	delete p1;
}

leftAdjust与此类似


void BTree::leftAdjust(Bnode* p, Bnode* q, int d, int j)//结点p与父节点q一起调整，d是最少阶数，j是父节点调整位置
{
	Bnode* p1 = q->child[j + 1];    //p的右兄弟
	if (p1->num > d - 1)          //右兄弟关键码足够分给p
	{
		p->num++;
		p->key[p->num] = q->key[j + 1];   //父节点相应关键码下沉
		q->key[j + 1] = p1->key[1];       //p1的最小关键码上移
		p->child[p->num] = p1->child[0];
		p1->child[0] = p1->child[1];
		compress(p1, 1);

	}
	else
		merge(p, q, p1, j + 1);
}

B树可视化

为了实现B树的可视化，一开始想要运用MFC或QT实现，但是这样太过于复杂，为了实现一棵树的可视化需要花费大量实践。之后在VS Code上发现一个专为数据结构可视化而生的脚本语言dot，语言逻辑简单，且安装也十分简便
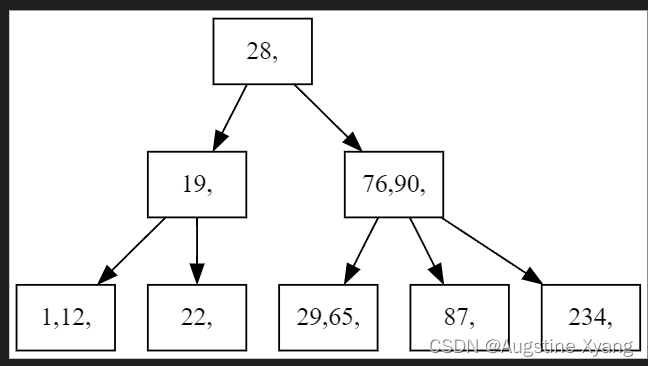
在这里插入图片描述
实际效果如图：
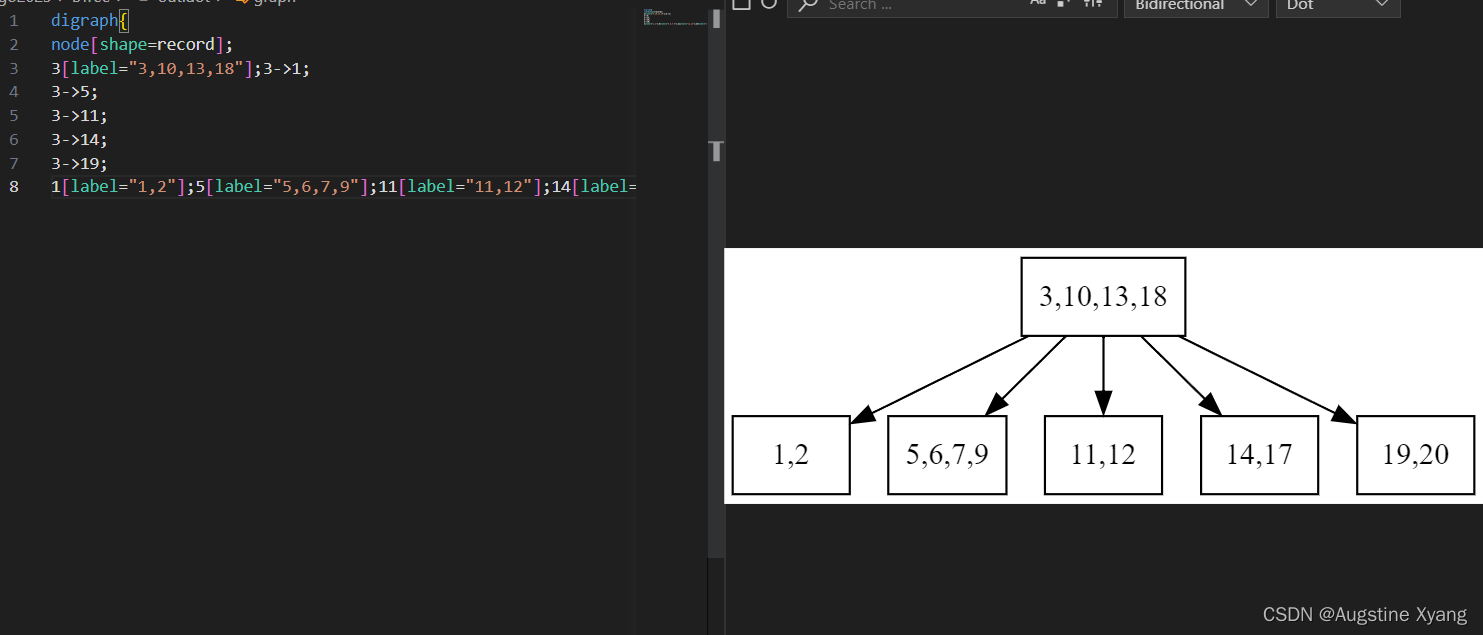
在这里插入图片描述

此处做简单说明：
· dot语言中3->1,3->14语句表示结点3指向结点1，结点3指向结点14。3、1、14即是结点的名字，而每个结点的[label=“…”]的label中则是每个结点的关键码内容。此处我简单使每个结点的名称是其第一个关键码，这样既可以保证不会重复，也会使写入dot文件时的流程更加简单。

代码方面：

void BTree::treePrint()
{

	ofstream out("out.dot", ios::out | ios::trunc);
	out << "digraph{" << endl << "node[shape=record];" << endl;
	root->printNode(out);
	out << "}";

}


void printNode(ofstream& out) {
		//cout << setw(space);
		//cout << "(";
		string name = to_string(key[1]); //第一个关键码做名称
		string str = name + "[label=\"";
		for (int i = 1; i <= num; i++)
		{
			str += to_string(key[i]);
			str += ",";
		}
		str += "\"];";
		out << str;

		for (int i = 0; i <= num; i++)  //实现该结点指向其子结点
		{
			if (child[i] != NULL) {
				out << name << "->" << child[i]->key[1] << ";" << endl;
			}
		}
		int i = 0;
		while (child[i] != NULL)
		{
			child[i]->printNode(out);  //递归调用
			i++;
		}

	}

使用说明

初始化

初始时，会需要输入初始的关键码个数和阶数，用于初始化B树：
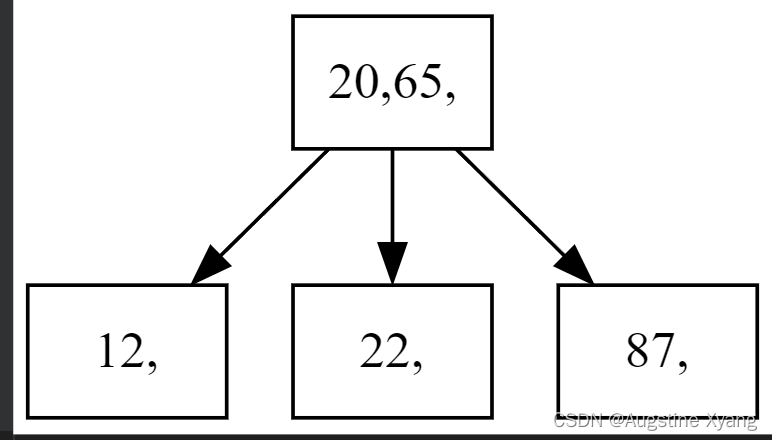
在这里插入图片描述
在这里插入图片描述

单次插入

输入I时，会执行insert插入关键码：
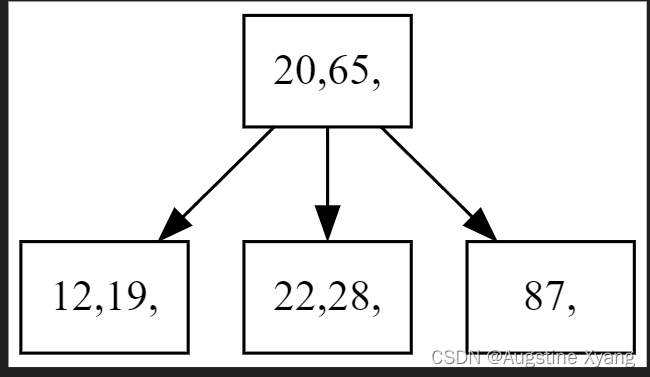
在这里插入图片描述
在这里插入图片描述

单次删除

输入D时，执行Delete删除操作
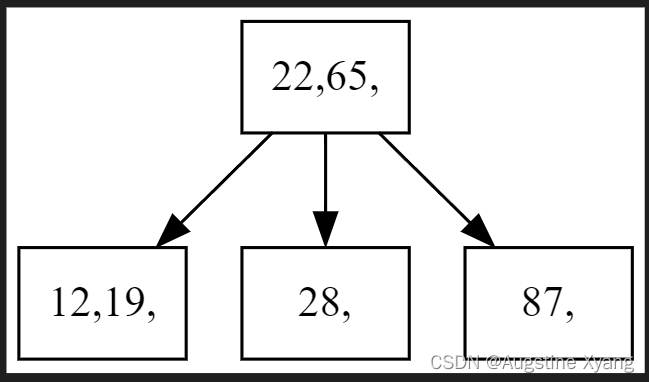
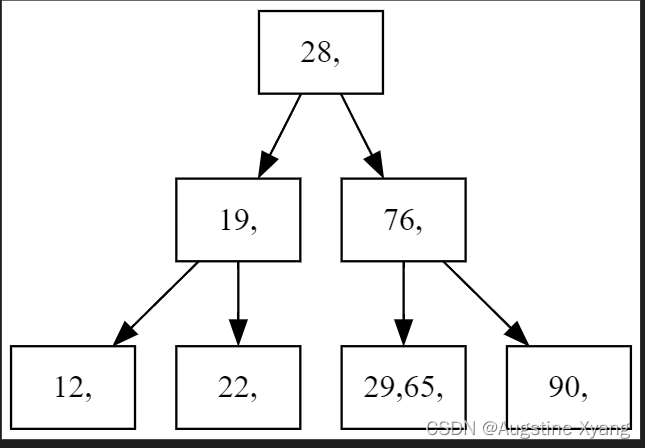
在这里插入图片描述
在这里插入图片描述

多插入

输入MI，执行multiInsert，一次性插入多个关键码，以以下格式输入：num，num，num……，num#：
在这里插入图片描述
会检测是否重复插入
在这里插入图片描述

多删除

输入MD，执行多个关键码的删除
在这里插入图片描述

在这里插入图片描述

Augstine Xyang
关注
  • 0
    点赞
  • 踩
  • 6
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
可视化B-树演示系统
01-03
可视化B-树演示系统，使用MFC制作，包括创建、删除、插入
AVL、B-TREE、B+TREE及算法可视化网站
IS_MOKE的博客
02-16 521
AVL、B-TREE、B+TREE及算法可视化网站
『数据结构与算法』B树图文详解（含完整代码）
人生就是一个不断学习的过程
12-30 1819
GitHub源码分享 微信搜索：码农StayUp 主页地址：https://gozhuyinglong.github.io 源码分享：https://github.com/gozhuyinglong/blog-demos 1. 前言 迄今为止，已经介绍了《 二叉查找树 》和《 AVL树 》，我们始终假设可以把整个数据结构存储在内存中。可是，如果数据多到内存装不下，这就意味着必须把数据放在磁盘上，显然这些数据结构不再适用。 问题在于磁盘的I/O速度是远远不如内存访问速度的，然而从一棵树中查找到某个元素，.
B树的原理及代码实现、B+树和B*树介绍及应用
weixin_61857742的博客
01-03 1863
B树主要用于磁盘文件的检索操作。众所周知，平衡二叉树（AVL树、红黑树）搜索的时间复杂度是O(log^n)。虽然很快，但如果数据在磁盘中且有上亿量级的数据，即便只有30次左右的IO操作，速度也是非常慢的。因为磁盘IO速度极慢，主要是寻道操作影响，平均8ms左右。因此，磁盘数据的检索不适合使用平衡二叉树，B树正式上线。B树可以看成是压缩版的平衡二叉树，每一个节点上都有保存有多个值，且有多个叶子节点。一般而言，B树的检索次数在个位量级，这取决于每个节点上能保存多少个值。
数据结构-B树的特点结构与C++实现
m0_61789994的博客
06-09 1675
B树，全称为B-树（B-tree），是一种自平衡的搜索树，由Rudolf Bayer和Edward McCreight于1972年提出。B树的设计目标是在磁盘等外部存储介质上进行高效的查找、插入和删除操作。B树的关键特点是它可以容纳多个子节点的节点，这使得B树可以充分利用外部存储介质的块读取能力，减少磁盘IO次数，提高访问效率。B树的节点通常会存储一组有序的键值对，用于进行数据的检索和排序。
一文看懂---B树及其简单实现
u014801954的博客
12-17 800
目录 1.B树的引入 2.B树的概念 3.B树是如何插入的？ B树性能分析： 4.具体的代码实现
基于QT实现B树可视化程序设计.zip
06-24
本例在实现基础功能的基础上，用QT做了B树的可视化： 1."/src/BTree"文件中的是原始代码，可以通过控制台对B树操作，并在控制台中可视化； 2."/src/BTreeDisplay"文件中是QT可视化工程代码。用对话框和QT绘制实现B树...
基于QT（C++）实现B树可视化【100010518】
01-28
本例在实现基础功能的基础上，用QT做了B树的可视化： 1."/src/BTree"文件中的是原始代码，可以通过控制台对B树操作，并在控制台中可视化； 2."/src/BTreeDisplay"文件中是QT可视化工程代码。用对话框和QT绘制实现B...
B+ Tree 增删改查 可视化
05-24
可视化增删改查数据
Python课程设计项目：基于python机器学习(ml)的天气预测和天气可视化+源代码+文档说明
最新发布
12-01
天气预测和天气可视化是一个基于python机器学习(ml)的长春地区的天气预报项目，它实现了天气数据的爬取，预测和可视化。 项目结构如下： ![img](image/wps26.jpg) * 天气数据的来源 GetData文件使用python爬虫...
cpp-QT实现B树可视化
08-16
QT实现B树可视化
B树基本操作flash动画演示
03-02
B树基本操作flash动画演示，很简单易懂
用Qt编写的B树的图形化显示
12-05
用Qt编写的B树的图形化显示，能够建立指定的B树，添加删除节点，一切都是图形化显示的。可用于B树的学习。
treap树VB实现
10-26
treap树算法实现，VB编写的代码，含可视化操作界面
B树的代码实现
一个小孩
04-16 901
B树的原理在这篇博客https://blog.csdn.net/xiaoan08133192/article/details/115622370中进行了介绍，这里是B树的代码实现。B树的插入和删除函数，在遍历的时候都是使用不回溯的方法，插入操作在对a结点插入数据的时，已经保证了a的关键字个数小于2*M - 1，删除操作在对a结点删除数据的时，已经保证了a的关键字个数大于M - 1。如何保证这一点是代码的精髓 //M为B树的最小度 #define M 2 typedef struct btree_node
B树实现代码
qq_42120843的博客
03-02 296
手撕B树
B树的代码实现和解析
jinzhi66的博客
04-18 1114
1.问题描述： (1)实现在B-树上的查找，并分析其时间复杂性。 (2)实现B-树的ADT，包括其上的基本操作：结点的加入和删除。 (3)要求B-树结构中的M=3或5，实现其中的一种即可。 (4)实现基本操作的演示。 2.模块划分 (1)初始化B树。 (2)查找操作。 (3)显示操作。 (4)插入操作 (5)删除操作。 (6)销毁操作。 3.代码部分 #ifndef _BTREE_H #define _BTREE_H #define MAXM 10
多叉树的可视化与遍历
dizuo的专栏
04-12 1万+
 最近忙着做毕设，其中的骨架系统说白了就是一个多叉层次树结构，当整体框架已经差不多的时候，就一直思考着重构一下代码，因为最初只是为了实现效果，所以有很多地方的设计不是很合理。 先自己写了一个多叉树的小型库，支持用迭代器创建，递归遍历，销毁，试着增加一些其他功能，例如给前序迭代器增加了operator++，但是发现很多地方受到了node结构的限制。多叉树的node数据结构如下：class N
C语言-B树（B-树）的完整实现
热门推荐
geek_jerome的博客
12-25 2万+
B树的定义 B树是一种平衡的多路查找树。 一颗m阶B树，或为空树，或为满足下列特性的m叉树。 （1）树中每个结点最多含有m棵子树; （2）若根结点不是叶子结点，则至少有两颗子树; （3）除根之外的所有非终端结点至少有[m/2]; （4）每个非终端结点中包含信息：（n,A0,K1,A1,K2,A2,…,Kn,An)。其中 ①Ki（1≤i≤n）为关键字，且关键字按升序排序。 ②指针Ai（
八叉树体素网格python可视化代码
05-22
以下是一个简单的八叉树体素网格python可视化代码示例： ```python from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt from octree import Octree # 创建八叉树 octree = Octree(50, 50, ...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值