游戏中常见的几种排序算法

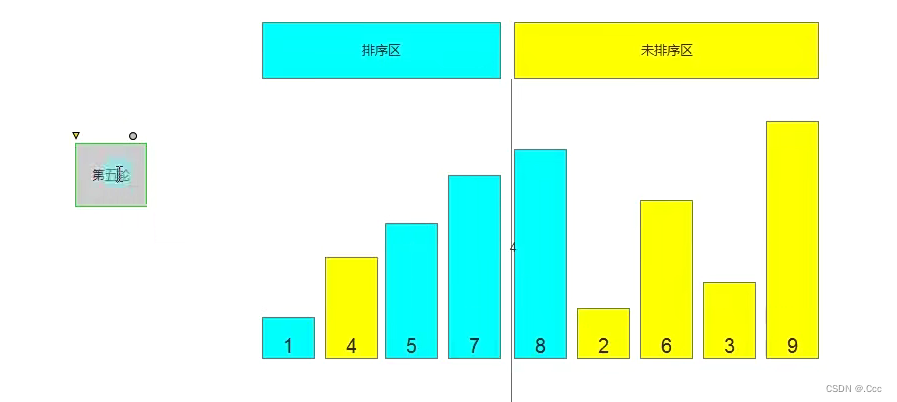
1.插入排序

两个区域  一个已排序区域和未排序区域，默认第一个元素是已排序区域，未排序的第一个元素和已排序的所有元素比较，已排序的元素大于这个第一个元素，已排序的元素就后移，未排序的就上去。

写法：       两个循环 一个for循环和while循环

                  两个变量 一个是已排序元素的索引值，一个是未排序元素的值

代码：

//插入排序
        public void charuSort(int[]a)
        {
            //两层循环 
            for (int i = 1; i < a.Length; i++)
            {
                //排序区的最后一个索引
                int sortIndex = i - 1;
                //未排序的第一个值
                int nosortValue = a[i];
                while (sortIndex >= 0 && a[sortIndex] > nosortValue)
                {
                    //这里是Index+1 和index  不是Inedx和Index-1 i会被赋值为-1
                    a[sortIndex + 1] = a[sortIndex];
                    sortIndex--;
                }
                a[sortIndex + 1] = nosortValue;
            }

        }

2.希尔排序

基于插入排序，多了一个步长的概念，默认步长是长度/2，后面就是步长/2，根据步长把原序列分成多个子序列，对子序列进行插入排序。一轮操作了所有序列。

写法：就是插入排序，每次移动1单位改成移动一步长

代码：

 //希尔排序
        public void  xierSort(int[] b)
        {
            //设置一个步长 根据步长来写
            for (int step = b.Length/2; step>0; step=step/2)
            {
                for (int i = step; i < b.Length; i++)
                {
                    int sortIndex = i - step;
                    int nosortValue = b[i];
                    while (sortIndex >= 0 && nosortValue < b[sortIndex])
                    {
                        b[sortIndex + step] = b[sortIndex];
                        sortIndex-=step;
                    }
                    b[sortIndex + step]= nosortValue;
                }  
            } 
            for (int i = 0; i < b.Length; i++)
                {
                    Console.WriteLine(b[i]);
                }
        }

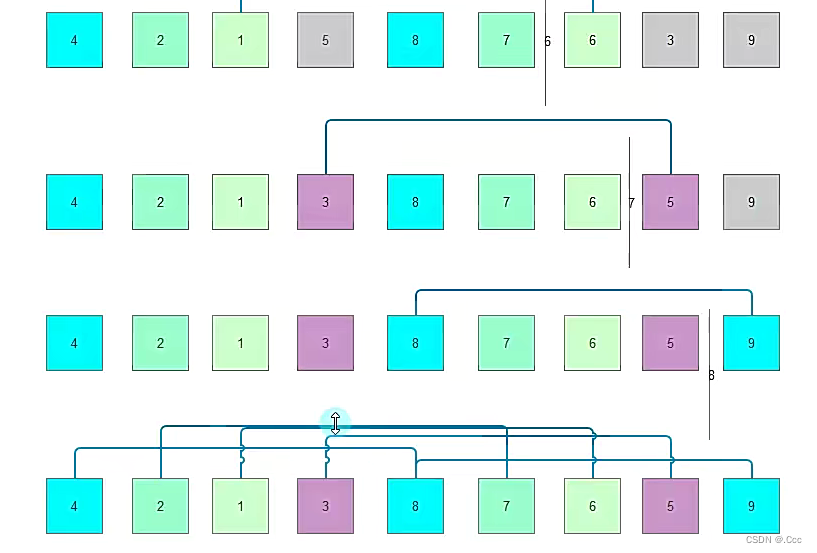
3.归并排序

就是递归加合并。

写法：一个排序函数，一个平分函数，平分函数里返回排序函数。

//归并排序
        public static int[] Sort(int[] left, int[] right)
        {
            //声明一个新数组存 左右比较后的元素
            int[] resArray = new int[left.Length + right.Length];
            int leftIndex = 0;
            int rightIndex = 0;
            //resArray要存满
            for (int i = 0; i < resArray.Length; i++)
            {
                //如果左边数组索引大于等于数组长度了 说明左边比较完了
                //这个时候右边就不用比较了 全部放入新数组中
                if (leftIndex >= left.Length)
                {
                    resArray[i] = right[rightIndex];
                    rightIndex++;
                }
                //与上述同理
                else if (rightIndex >= right.Length)
                {
                    resArray[i] = left[leftIndex];
                     leftIndex++;
                }
                //左边比右边大 右边进新数组
                //右边索引+1
                else if (left[leftIndex] > right[rightIndex])
                {
                    resArray[i] = right[rightIndex];
                    rightIndex++;
                }
                //与上述同理
                else
                {
                    resArray[i] = left[leftIndex];
                    leftIndex++;
                }
            }
            return resArray;
        }
        public static int[] guibingSort(int[] c)
        {
            //递归结束
            //数组长度小于2 不能再分了
            if (c.Length < 2)
            {
                return c;
            }
            int mid = c.Length / 2;
            //声明左右数组
            int[] leftArray = new int[mid];
            int[] rightArray = new int[c.Length - mid];
            //初始化左右数组
            for (int i = 0; i < c.Length; i++)
            {
                if (i < mid)
                {
                    leftArray[i] = c[i];
                }
                else
                {
                    rightArray[i - mid] = c[i];
                }
            }
            //这里返回排序函数
            return Sort(guibingSort(leftArray), guibingSort(rightArray));
        }
    }

4.快速排序

快排的优化：

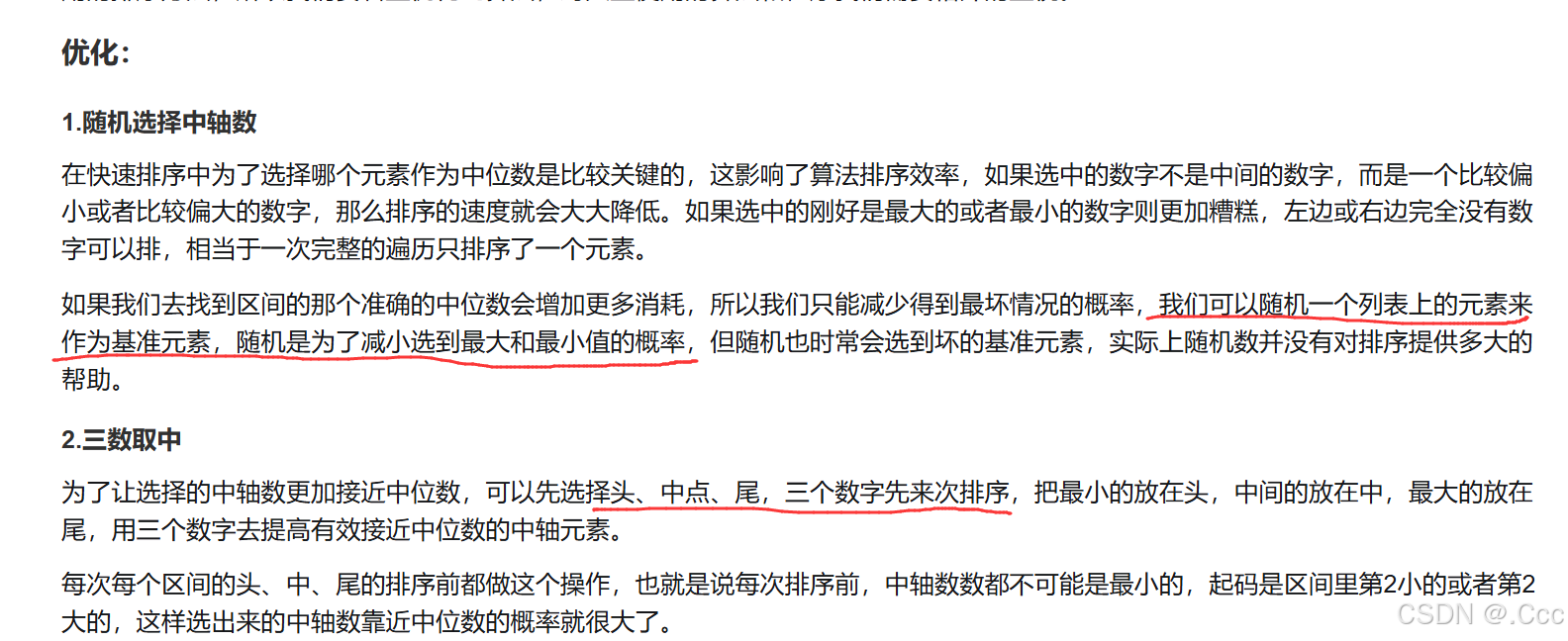
类似归并排序 有递归 分数组 

三个变量 分别是一个基准值 一个lefttmp 一个righttmp  三个while循环

  //快速排序
        public static void QuickSort(int[]d,int left,int right)
        {
            //递归出口
            if(left >= right)
            {
                return;
            }
            int lefttmp, righttmp, temp;
            temp = d[left];
            lefttmp = left;
            righttmp= right;
            //lefttmp 、righttmp 这两个一直在变 所以条件是这两个
            while (lefttmp != righttmp)
            {
                //从右边开始看 右边的值小于基准值就放到左边去
                while (lefttmp < righttmp&& d[righttmp] > temp)
                {
                    righttmp--;
                }
                //循环结束后就是满足条件的 交换
                d[lefttmp] = d[righttmp];
                //同理 上述
                while ( lefttmp < righttmp&& d[lefttmp] < temp)
                {
                    lefttmp++;
                }
                d[righttmp] = d[lefttmp];
            }
                d[lefttmp]=temp;
            //下一轮
            QuickSort(d,left,righttmp-1);
            QuickSort(d, lefttmp+1, right);
        }

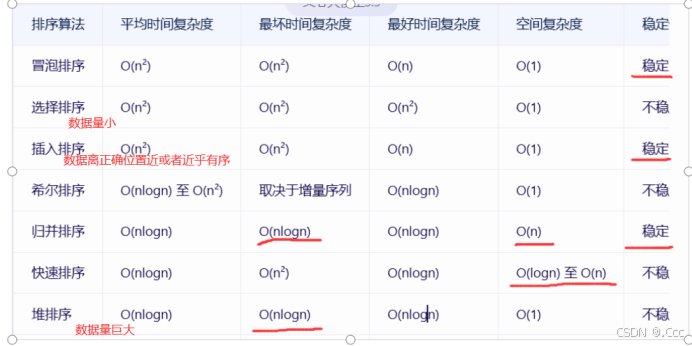
5.堆排序

用数组建立起一个堆的概念，建立一个大顶堆（找最大的非叶子节点（length/2-1），然后和它的子节点(2*i+1,2*i+2)比较，最大的放顶(有放顶操作可能导致原来的父子节点顺序不对，需要再次比较))

稳定性：相等元素排序后的相对顺序是否发生变化