DVB-S学习记录之信道编码

经过信源编码和系统复接后生成的节目传送码流，通常需要通过某种传输媒 介才能到达用户接收机。通常情况下，编码码流并不能直接通过信道传输，必须经过信道编码后，使其变成适合在信道中传输的形式后再进行传输。

DVB-S的信道编码主要包括

• 扰码
• R-S编码
• 卷积交织
• 卷积编码

扰码

数字通信理论在设计通信系统时都是假设传输比特流中 0 和 1 的出现概率是等概的，实际中的通信系统的设计指标等首先也是以该假设为前提的。

但是TS（transport stream）码流经过编码后可能会出现连0或连1的情况，一方面破坏了系统设计的前提，另一方面连0或连1会使得比特时钟的提取变得困难，因此，为保证在任何情况下进入 DVB 传输系统的数据码流中"0"与"1"的概率都能基本相等，系统引入一个伪随机序列对TS码流进行扰乱处理，使得 0 和 1 的出现概率接近50%。

扰乱改变了原 TS 码流，因此在接收端对传输码流纠错解码后，还需 按逆过程对其进行解扰处理，以恢复原 TS 码流。

在接收端对接收到的码流逆编码后，就可以恢复原TS码流

原理

传送复用器输出的TS流帧结构如图所示：

第一个字节为同步字节，数值为47H。每8个包组成一个超帧，并将第一个包的同步字节反转，变为B8H，后面的7个包的同步字节不变。同步字节不参与扰码，其余字节参与扰码

伪随机二进制序列（PRBS）生成器的多项式应为：

$$P(X)=1+X^{14}+X^{15}$$

其扰码过程如图所示：

扰码输出如下图所示：

R-S编码

DVB-S中使用的外层纠错编码为R-S（204，188）码，编码效率 $ R_c=\frac{188}{204}=0.92 $ , 码字长度为8。

每个TS包独立进行R-S编码保护，生成一个R-S码字，R-S同步头就采用TS的包头，如此设计有以下好处：

1. 当某个 R-S 码字在接 收端解码时出现无法纠正的错误时，误码集中在一个 TS 包中，不会影响到其它的TS 包，便于分接器进行差错指示
2. 便于分接器提取 TS 包的同步，简化了 TS 包同步提取系统结构

R-S码字结构

编码原理

对于定义在$GF(2^m)$的RS(n,k)码，$n=2^m-1$ ，生成多项式取

$$g(x)=\prod _{i=1}^{i=n-k}(x+{\alpha }^i)=x^{2t}+g_{2t-1}{x}^{2t-1}+\cdots +g_2{x}^2+g_{1}x+g_0$$

记 $ n-k=2t $ ，纠错能力为$t$，就是说如果编码后的一组数据里面出现了错误的数据个数不大于 t，那么可以通过 n-k 个监督数据达到对错误数据纠正的目的

$g(x)$的系数属于$GF(2^m)$ ,生成矩阵 G 可表示为:

$$G=\left[\begin{array}{cccccccc}{\mathrm{g}}_{2t}& {\mathrm{g}}_{2t-1}& \cdots & {\mathrm{g}}_1& {\mathrm{g}}_0& 0& \cdots & 0\\ 0& {\mathrm{g}}_{2t}& \cdots & {\mathrm{g}}_2& {\mathrm{g}}_1& {\mathrm{g}}_0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\mathrm{g}}_{2t}& {\mathrm{g}}_{2t-1}& {\mathrm{g}}_{2t-2}& \cdots & {\mathrm{g}}_0\end{array}\right]$$

对矩阵 G 进行变换得到与其等价的矩阵 G_1 ，该矩阵由 k阶单位矩阵 $ \bold I $ 和 $k*(n-k) $ 阶的矩阵 $ \bold A $ 组成 ，满足
$$G_1=[I|A]=\left[\begin{array}{cccccccc}1& 0& \cdots & 0& a_{1,1}& a_{1,2}& \cdots & a_{1,n-k}\\ 0& 1& \cdots & 0& a_{2,1}& a_{2,2}& \cdots & a_{2,n-k}\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1& a_{k,1}& g_{k,2}& \cdots & a_{k,n-k}\end{array}\right]$$

编码结果可以表示为

$$C=U\cdot G_1=[U|U\cdot A]=[U|R]$$

其中矩阵 $ \bold R $ 有$n-k$个监督符号，多项式表示为

$$r(x)=r_{n-k-1}{x}^{n-k-1}+\cdots +r_2{x}^2+r_{1}x+r_0$$

因此经过R-S编码后的码多项式为

$$c(x)=u(x)x^{n-k}+r(x)$$

DVB-S使用的R-S生成多项式为
$$G(X)=\coprod ^{15}(X+{\lambda }^i)$$

其中 $ \lambda =02H $ ，为本原元，域生成多项式为
$$P(X)=X^8+X^4+X^3+X^2+1$$
最小码距为17字节

R-S(204，188，T=8)码帧结构

卷积交织

在编码后加上卷积交织，使得数据的传送顺序按照一定的规律分散开，这样可以使信道中突发性干扰造成的错误字符也被分散开来。

DVB-S 中交织采用卷积交织的方式，其交织深度为 204/17=12 ，下图为交织和解码的原理图

它由FIFO组成，数据按行写入寄存器，按列读出。

交织过程如下：R-S 编码码字向第 0 到第 11 支路依次循环输入数据，每条支路每次输入一个字节，交织后的数据按相同的顺序从各支路中输出，每条支路每次输出一个字节。R-S 码字的同步头永远从第 0 支路，即无延时支路传送。这样交 织后的数据流依然保持了 R-S 码字的同步和长度

假设输入的数据为从小到大的自然数，输入的数据如下

1	2	3	4	5	6	7	8	9	10	11	12
13	14	15	16	17	18	19	20	21	22	23	24
25	26	27	28	29	30	31	32	33	34	35	36
37	38	39	40	41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70	71	72
73	74	75	76	77	78	79	80	81	82	83	84
85	86	87	88	89	90	91	92	93	94	95	96
97	98	99	100	101	102	103	104	105	106	107	108
109	110	111	112	113	114	115	116	117	118	119	120
121	122	123	124	125	126	127	128	129	130	131	132
133	134	135	136	137	138	139	140	141	142	143	144
145	146	147	148	149	150	151	152	153	154	155	156
157	158	159	160	161	162	163	164	165	166	167	168
169	170	171	172	173	174	175	176	177	178	179	180
181	182	183	184	185	186	187	188	189	190	191	192
193	194	195	196	197	198	199	200	201	202	203	204
205	206	207	208	209	210	211	212	213	214	215	216
217	218	219	220	221	222	223	224	225	226	227	228

经过交织模块后可以得到如下输出：

1	0	0	0	0	0	0	0	0	0	0	0
13	0	0	0	0	0	0	0	0	0	0	0
25	0	0	0	0	0	0	0	0	0	0	0
37	0	0	0	0	0	0	0	0	0	0	0
49	0	0	0	0	0	0	0	0	0	0	0
61	0	0	0	0	0	0	0	0	0	0	0
73	0	0	0	0	0	0	0	0	0	0	0
85	0	0	0	0	0	0	0	0	0	0	0
97	0	0	0	0	0	0	0	0	0	0	0
109	0	0	0	0	0	0	0	0	0	0	0
121	0	0	0	0	0	0	0	0	0	0	0
133	0	0	0	0	0	0	0	0	0	0	0
145	0	0	0	0	0	0	0	0	0	0	0
157	0	0	0	0	0	0	0	0	0	0	0
169	0	0	0	0	0	0	0	0	0	0	0
181	0	0	0	0	0	0	0	0	0	0	0
193	0	0	0	0	0	0	0	0	0	0	0
205	2	0	0	0	0	0	0	0	0	0	0
217	14	0	0	0	0	0	0	0	0	0	0

因此，在卷积交织的输出序列中，同一个误码包的任意两个字节的最小距离为12字节，所以，R-S(204,188,T=8)编码加上卷积交织后纠错的最大字节长度为 $ 8\times12=96 $ ，大大提高系统的纠错能力。

卷积编码

DVB-S的内码编码采用收缩卷积编码，系统框图如下

中间的方框代表一个7位的移位寄存器，两个输出X、Y的生成多项式分别为
$$\begin{array}{rl}{G}_1& =1+X+X^2+X^3+X^6\\ & \\ G_2& =1+X^2+X^3+X^5+X^6\end{array}$$
该系统每个clk输入1bit信息，有两个模2加法器输出2bit信息，且输出的信息和移位寄存器内的当前信息和前6个信息都有关系，因此常用(2，1，7)来表示该卷积码

QPSK

数字信号理论频谱带宽无限宽，要想无失真的传输数字信号，要在无限带宽信道中传输，而卫星系统的信道是带限信道，因此需要对卷积编码模块输出的信号进行成型滤波，使其与卫星信道匹配。

基带成型滤波器一方面要降低传输中需要的带宽，另一方面使码间串扰降至最低。理论上来说，如果随机数字码元流的重复周期为 Ts，只要通过带宽为π/Ts 的理想滤 波器后，在 $nTs$ 时刻抽样，无码间干扰。由于理想LPF难以实现，因此选用升余弦滚降滤波器，传输函数为

的升余弦滚降滤波器满足要求

$f_N=\frac{1}{2T_s}=\frac{R_s}{2}$为奈奎斯特频率

传输带宽$B_r=\frac{1=\alpha }{2T_s}Hz$

频带利用率$\eta =\frac{R_s}{B_r}=\frac{2}{1+\alpha }bit/Hz$

在DVB-S系统中滚降系数$\alpha =0.35$

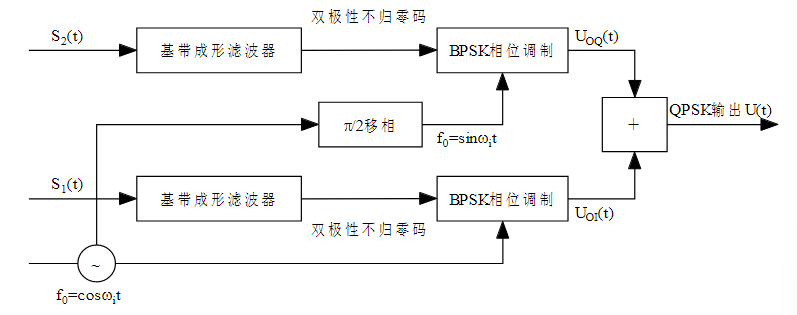
下图为QPSK调制框图：