A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.
For example, a greedy strategy for the travelling salesman problem (which is of high computational complexity) is the following heuristic: “At each step of the journey, visit the nearest unvisited city.” This heuristic does not intend to find the best solution, but it terminates in a reasonable number of steps; finding an optimal solution to such a complex problem typically requires unreasonably many steps. In mathematical optimization, greedy algorithms optimally solve combinatorial problems having the properties of matroids and give constant-factor approximations to optimization problems with the submodular structure.
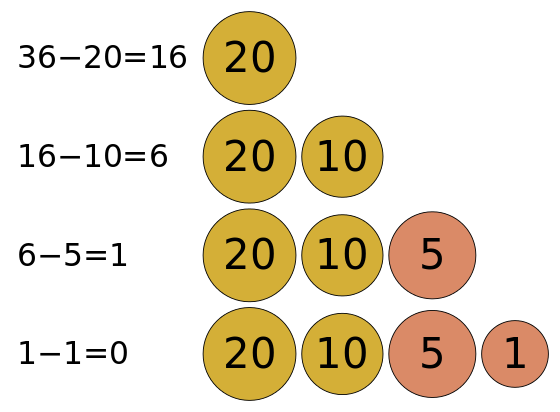
Greedy algorithms determine the minimum number of coins to give while making change. These are the steps most people would take to emulate a greedy algorithm to represent 36 36 36 cents using only coins with values { 1 , 5 , 10 , 20 1, 5, 10, 20 1,5,10,20}. The coin of the highest value, less than the remaining change owed, is the local optimum. (In general, the change-making problem requires dynamic programming to find an optimal solution; however, most currency systems are special cases where the greedy strategy does find an optimal solution.)
Contents
1 Specifics
Greedy algorithms produce good solutions on some mathematical problems, but not on others. Most problems for which they work will have two properties:
Greedy choice property
We can make whatever choice seems best at the moment and then solve the subproblems that arise later. The choice made by a greedy algorithm may depend on choices made so far, but not on future choices or all the solutions to the subproblem. It iteratively makes one greedy choice after another, reducing each given problem into a smaller one. In other words, a greedy algorithm never reconsiders its choices. This is the main difference from dynamic programming, which is exhaustive and is guaranteed to find the solution. After every stage, dynamic programming makes decisions based on all the decisions made in the previous stage and may reconsider the previous stage’s algorithmic path to the solution.
Optimal substructure
“A problem exhibits optimal substructure if an optimal solution to the problem contains optimal solutions to the sub-problems.”[2]
1.1 Cases of failure
Greedy algorithms fail to produce the optimal solution for many other problems and may even produce the unique worst possible solution. One example is the travelling salesman problem mentioned above: for each number of cities, there is an assignment of distances between the cities for which the nearest-neighbour heuristic produces the unique worst possible tour.[3] For other possible examples, see horizon effect.

























 506
506

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








