洛必达法则

目录

洛必达法则

 例题：

无穷比无穷洛必达法则的应用

洛必达法则的使用条件：

---

我们先使用柯西中值定理举一个例子

 

 我们引入洛必达法则：

洛必达法则

 三个条件：极限值为0，可导，比值的导数存在。

得出的结论：比值的极限等于比值导数的极限。

我们进行证明：

 例题：

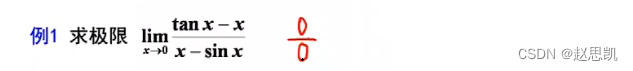
这个极限是0比0的形式，我们可以考虑使用洛必达，我们需要考虑是否满足洛必达法则：

 

 对于洛必达法则的前两条我们不需要判定，我们只需要判定第三条即可

 极限值存在或者极限值为无穷大。

 

 

 极限结构为0/0

我们先进行化简：

无穷比无穷洛必达法则的应用

对于无穷比无穷，我们也可以使用洛必达法则：

例如：

 

 

 得出的结论：

当对数函数，幂函数，指数函数的自变量全部趋向于无穷时，谁趋向于无穷的速度更快呢？

答：指数函数大于幂函数大于对数函数 

 遇到这类无穷减去无穷的问题，我们可以先通分

 

 无穷减无穷的处理方法：先同分，再使用等价无穷小化简，最后使用洛必达法则。

 这种形式是0的0次方：

遇到这类问题，我们主要用e来进行解决：

 对于0的0次方的问题，首先使用指数函数e来进行代换，转换为0乘无穷的问题，然后判断求导是否复杂，复杂时使用等价代换，之后使用洛必达法则。

 这里是1的无穷大次方：

 对于1的无穷大次方，我们也转换成e的指数函数的形式，使用洛必达法则求极限。

洛必达法则的使用条件：

导数的极限存在或者导数的极限等于无穷大

 例如：