说明:本文采用了一个三层 BP 网络来拟合 s i n ( x ) sin(x) sin(x) 和其他的一些简单函数,并且训练集和测试集都是生成的随机数,在拟合更加复杂的模型时需要进行相应的数据预处理、正则化或归一化操作,同时调整网络的超参。
一、BP 网络原理简介
什么是 BP 网络?
人工神经网络可以通过自身的训练,寻找并学习训练集中给定输入值和期望输出值之间的关系,从而总结出某些规则,并以此在应用过程中根据用户的输入得到一个合适的输出值。这些规则可以是为我们所知的,也有可能是未知的,神经网络的训练过程是一个黑盒操作,我们通过损失函数的变化、网络在测试集上的表现等等来判断一个网络的优劣。
BP 网络通过前向计算、反向传播两个简单的过程,利用梯度下降方法,逐步更新网络中的参数矩阵,从而实现对函数的拟合等其他任务。下图是一个三层神经网络的基本结构。
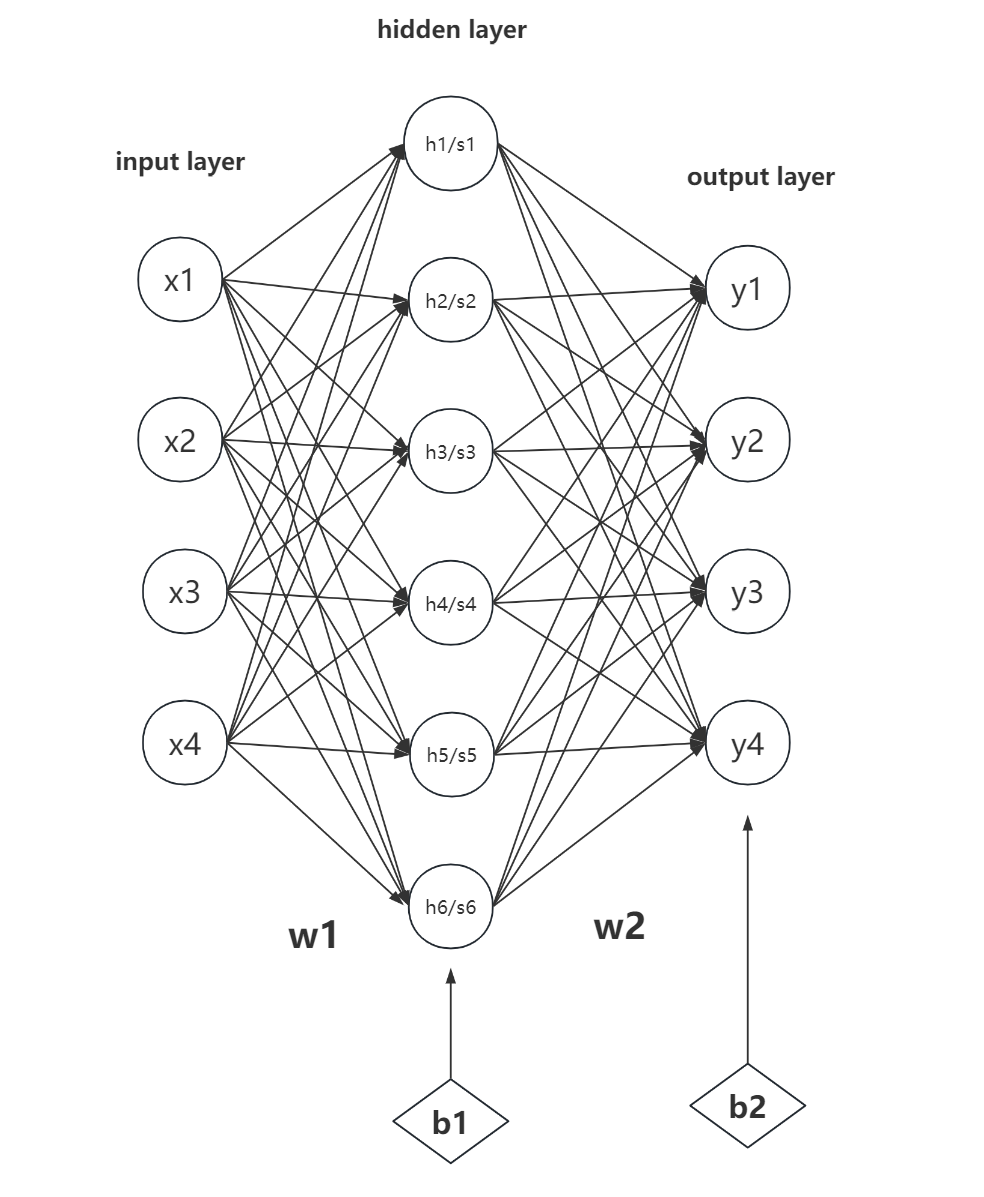
- input layer:输入层,可以输入一个向量。
- hidden layer:隐藏层/中间层,用来扩展输入向量的维度,对输入向量中蕴含的信息进行重排与组合,并在后面的反向转播过程中改进自己的组合方式以学习到我们期望的规律。hidden layer 可以不止一层,但是层数过多可能会出现梯度消失等问题。
- output layer:输出层。
BP 网络数学原理推导
前向计算过程:
在前向传播过程中,我们需要将输入的向量乘以一个变换矩阵来实现线性组合,该矩阵也可以称为权重矩阵,因为该矩阵中的数字代表了输入层中相应神经元蕴含的信息在变化过程中的重要程度。
以 h1 为例, h 1 = x 1 w 11 + x 2 w 21 + x 3 w 31 + x 4 w 41 h_1 = x_1w_{11}+x_2w_{21}+x_3w_{31}+x_4w_{41} h1=x1w11+x2w21+x3w31+x4w41,从这个式子中很容易看出 w 的权重作用。
应用到所有神经元,我们有:
h = x ⋅ w 1 \boldsymbol h = \boldsymbol x · \boldsymbol w_1 h=x⋅w1
由于该组合是线性的,这意味着神经网络中的数据与输入始终都是线性关系,这就无法实现非线性函数的拟合。因此我们需要加一个激活函数 sigmoid,用来将线性数据转换为非线性。同时在做 sigmoid 操作之前需要加上一个偏置向量 b1 来提高拟合模型的灵活性。
s i g m o i d : σ ( x ) = 1 1 + e − x sigmoid:\sigma(x) = {1\over 1+e^{-x}} sigmoid:σ(x)=1+e−x1
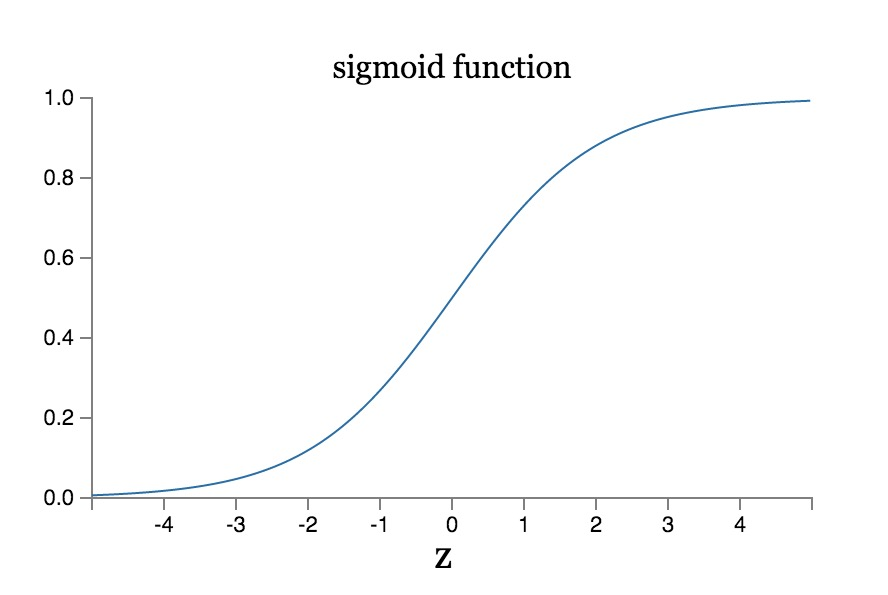
sigmoid 函数也具有一个很好的特性: σ ′ ( x ) = σ ( x ) [ 1 − σ ( x ) ] \sigma^{'}(x) = \sigma(x)[1-\sigma(x)] σ′(x)=σ(x)[1−σ(x)],这一点将会为后续梯度下降过程中的计算带来便利。
回到前向传播过程上来,我们有:
s = s i g m o i d ( h + b 1 ) \boldsymbol s = sigmoid(\boldsymbol h + \boldsymbol b_1) s=sigmoid(h+b1)
对 hidden layer 做相似的操作,只不过这次由升维改为了降维:
y = s ⋅ w 2 + b 2 \boldsymbol y = \boldsymbol s · \boldsymbol w_2 + \boldsymbol b_2 y=s⋅w2+b2
注意到输出层不要 sigmoid,因为 sigmoid 会把所有的负值转换成正值,显然没法拟合 s i n ( x ) sin(x) sin(x) 这种有负值的函数。
这样我们就得到了输出的向量。接下来就是根据输出与期望输出之间的差值来调整网络中的权重矩阵。
反向传播过程:
如何量化网络的输出与我们期望输出之间的差值?我们可以用 MSE(均方误差) 来定义损失函数。
MSE: l o s s = Σ 1 2 ( d i − y i ) 2 loss = \Sigma \frac12(d_i- y_i)^2 loss=Σ21(di−yi)2,其中 d d d 为期望输出, i i i 为输出层的一个神经元索引。
故 :
∂ ( l o s s ) ∂ y = y − d \frac {\partial (loss)}{\partial \boldsymbol y} = \boldsymbol y-\boldsymbol d ∂y∂(loss)=y−d
∂ ( l o s s ) ∂ w 2 = \frac {\partial (loss)}{\partial \boldsymbol w_2} = ∂w2∂(loss)= ∂ ( l o s s ) ∂ y ⋅ ∂ y ∂ w 2 \frac {\partial (loss)}{\partial \boldsymbol y}·\frac {\partial \boldsymbol y}{\partial \boldsymbol w_2} ∂y∂(loss)⋅∂w2∂y
又 ∂ y ∂ w 2 = ∂ ∂ w 2 ( w 2 ⋅ s + b 2 ) = s \frac{\partial \boldsymbol y}{\partial \boldsymbol w_2} = \frac{\partial}{\partial \boldsymbol w_2} (\boldsymbol w_2 \cdot \boldsymbol s+\boldsymbol b_2) = \boldsymbol s ∂w2∂y=∂w2∂(w2⋅s+b2)=s
所以 ∂ ( l o s s ) ∂ w 2 = s ⋅ ( y − d ) \frac{\partial(loss)}{\partial\boldsymbol w_2}=\boldsymbol s·(\boldsymbol y-\boldsymbol d) ∂w2∂(loss)=s⋅(y−d)
同理,
∂ ( l o s s ) ∂ b 2 = ∂ ( l o s s ) ∂ y ⋅ ∂ y ∂ b 2 = y − d \frac {\partial(loss)}{\partial \boldsymbol b_2} = \frac {\partial(loss)}{\partial \boldsymbol y}·\frac{\partial \boldsymbol y}{\partial \boldsymbol b_2} = \boldsymbol y -\boldsymbol d ∂b2∂(loss)=∂y∂(loss)⋅∂b2∂y=y−d
∂ ( l o s s ) ∂ w 1 = ∂ ( l o s s ) ∂ y ⋅ ∂ y ∂ s ⋅ ∂ s ∂ w 1 = ( y − d ) ⋅ w 2 ⋅ x ⋅ σ ′ ( s ) = ( y − d ) ⋅ w 2 ⋅ x ⋅ σ ( s ) ( 1 − σ ( s ) ) \frac {\partial (loss)}{\partial \boldsymbol w_1} = \frac{\partial (loss)}{\partial \boldsymbol y}·\frac{\partial \boldsymbol y}{\partial\boldsymbol s}·\frac{\partial\boldsymbol s}{\partial\boldsymbol w_1}=(\boldsymbol y-\boldsymbol d)·\boldsymbol w_2·\boldsymbol x ·\sigma'(\boldsymbol s) =(\boldsymbol y-\boldsymbol d)·\boldsymbol w_2·\boldsymbol x ·\sigma(\boldsymbol s)(1-\sigma(\boldsymbol s)) ∂w1∂(loss)=∂y∂(loss)⋅∂s∂y⋅∂w1∂s=(y−d)⋅w2⋅x⋅σ′(s)=(y−d)⋅w2⋅x⋅σ(s)(1−σ(s))
∂ ( l o s s ) ∂ b 1 = ∂ ( l o s s ) ∂ y ⋅ ∂ y ∂ s ⋅ ∂ s ∂ b 1 = ( y − d ) ⋅ w 2 \frac {\partial (loss)}{\partial \boldsymbol b_1} = \frac{\partial (loss)}{\partial \boldsymbol y}·\frac{\partial \boldsymbol y}{\partial\boldsymbol s}·\frac{\partial\boldsymbol s}{\partial\boldsymbol b_1}=(\boldsymbol y-\boldsymbol d)·\boldsymbol w_2 ∂b1∂(loss)=∂y∂(loss)⋅∂s∂y⋅∂b1∂s=(y−d)⋅w2
由此我们得到了损失函数关于网络中几个超参的偏导,组合起来也就成为了所谓的梯度。现在我们要应用梯度下降法调整超参,使得损失函数朝着减小的方向进行。注意减小的方向是梯度的反向。
Δ w 2 = r ⋅ s ⋅ ( y − d ) \Delta \boldsymbol w_2 = r·\boldsymbol s·(\boldsymbol y-\boldsymbol d) Δw2=r⋅s⋅(y−d)
Δ b 2 = r ⋅ ( y − d ) \Delta\boldsymbol b_2 = r·(\boldsymbol y -\boldsymbol d) Δb2=r⋅(y−d)
Δ w 1 = r ⋅ ( y − d ) ⋅ w 2 ⋅ x ⋅ σ ( s ) ( 1 − σ ( s ) ) \Delta \boldsymbol w_1 = r·(\boldsymbol y-\boldsymbol d)·\boldsymbol w_2·\boldsymbol x ·\sigma(\boldsymbol s)(1-\sigma(\boldsymbol s)) Δw1=r⋅(y−d)⋅w2⋅x⋅σ(s)(1−σ(s))
Δ b 1 = r ⋅ ( y − d ) ⋅ w 2 \Delta \boldsymbol b_1 = r·(\boldsymbol y-\boldsymbol d)·\boldsymbol w_2 Δb1=r⋅(y−d)⋅w2
其中
r
r
r 为 learning_rate 。
二、应用 BP 网络拟合一元非线性函数
在代码我以
s
i
n
(
x
)
sin(x)
sin(x) 为例,拟合其他函数可以修改 target_function() 实现。
代码如下:
import numpy as np
from matplotlib import pyplot as plt
# 定义 sigmoid 函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 定义 sigmoid 函数的导数
def sigmoid_derivative(x):
return x * (1 - x)
# 定义目标函数(sin 函数)
def target_function(x):
return np.sin(x)
# 定义神经网络参数
input_size = 1
hidden_size = 12
output_size = 1
learning_rate = 0.1
# 定义函数拟合过程
def funcFitting():
np.random.seed(0) # 固定 random.seed() 可以使得每次生成的随机数都一样,方便在出错时寻找问题
train_set = np.zeros((100, input_size))
# 生成训练数据
for i in range(len(train_set)):
train_set[i] = np.random.uniform(-np.pi, np.pi)
# 初始化权重和偏置
w1 = np.random.uniform(-10, 10, size=(input_size, hidden_size))
b1 = np.random.uniform(-10, 0, size=(1, hidden_size))
w2 = np.random.uniform(-10, 10, size=(hidden_size, output_size))
b2 = np.random.uniform(-10, 0, size=(1, output_size))
for epoch in range(1000):
for i in range(len(train_set)):
x = train_set[i]
x = np.array(x).reshape(1, input_size)
d = target_function(x)
h = x @ w1 + b1
s = sigmoid(h)
y = s @ w2 + b2
e = y - d
d_b2 = e
d_w2 = s.T * e
d_b = e @ w2.T * sigmoid_derivative(s)
d_w1 = x.T * d_b
b2 -= learning_rate * d_b2
w2 -= learning_rate * d_w2
b1 -= learning_rate * d_b
w1 -= learning_rate * d_w1
loss = np.mean(np.square(y - d))
print("Epoch:", epoch, "Loss:", loss)
test_set = np.zeros((10000, 1))
correct_num = 0
for i in range(len(test_set)):
test_set[i] = np.random.uniform(-np.pi, np.pi)
x_test = test_set[i]
x_test = np.array(x_test).reshape(1, input_size)
d_test = target_function(x_test)
h_test = x_test @ w1 + b1
s_test = sigmoid(h_test)
y_test = s_test @ w2 + b2
if np.mean(np.square(y_test - d_test)) < 0.01:
correct_num += 1
print("Accuracy:", correct_num / 100, "%")
# 绘制拟合结果
x_plot = np.linspace(-np.pi, np.pi, 100).reshape(-1, 1)
h_plot = x_plot @ w1 + b1
s_plot = sigmoid(h_plot)
z_plot = s_plot @ w2 + b2
d_plot = target_function(x_plot)
plt.plot(x_plot, d_plot, label="Actual")
plt.plot(x_plot, z_plot, label="Fitted")
plt.legend()
plt.show()
if __name__ == "__main__":
funcFitting()
下面是一些函数的拟合结果以及对应的超参(由于是一元函数,input_size 和output_size 都为 1,范围均为 ( − π , π ) (-\pi,\pi) (−π,π)):
-
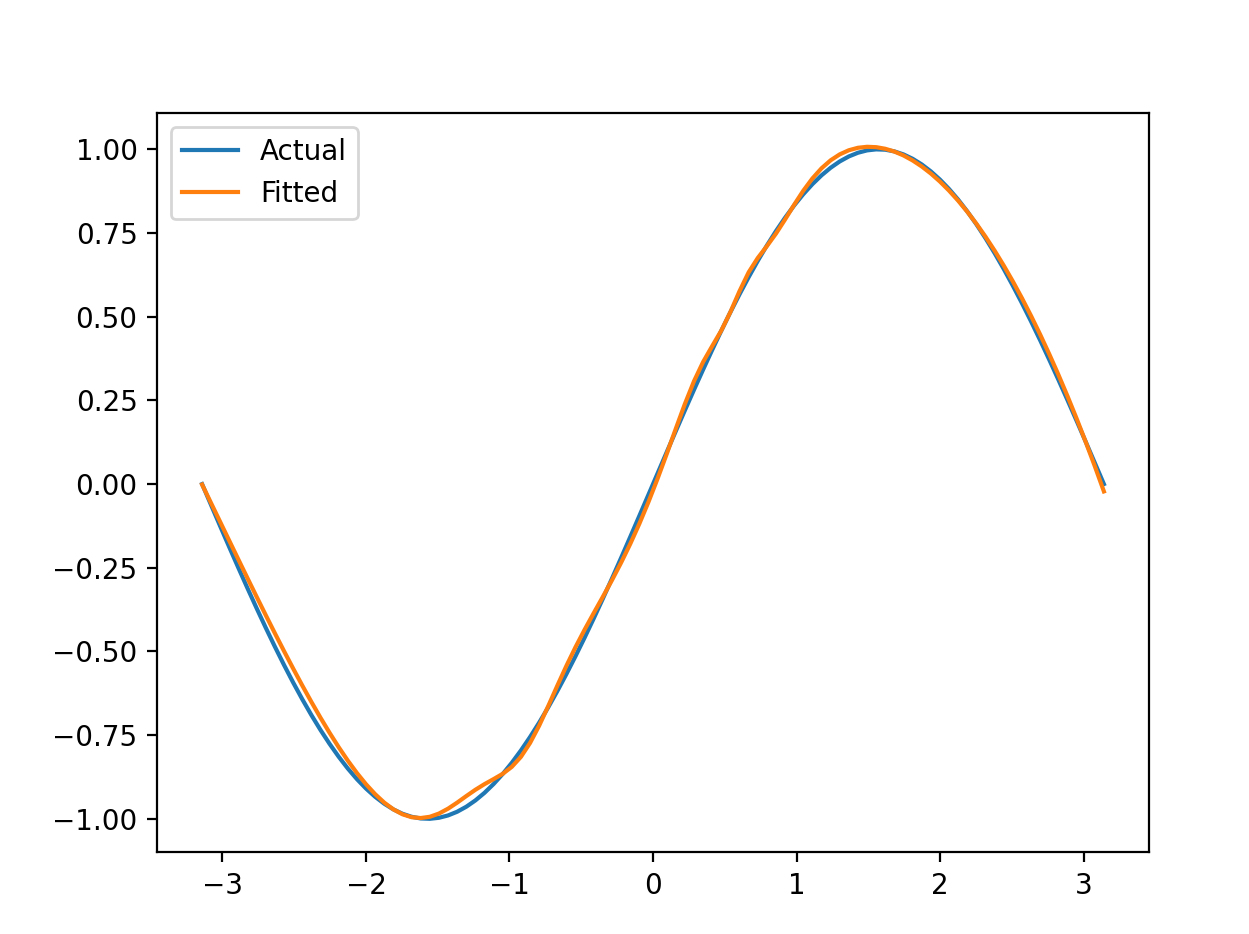
s i n ( x ) sin(x) sin(x):
hidden_size:12,epoch:1000,learn_rate:0.1测试集正确率:89.59%,允许误差: ± 0.001 \pm 0.001 ±0.001
-
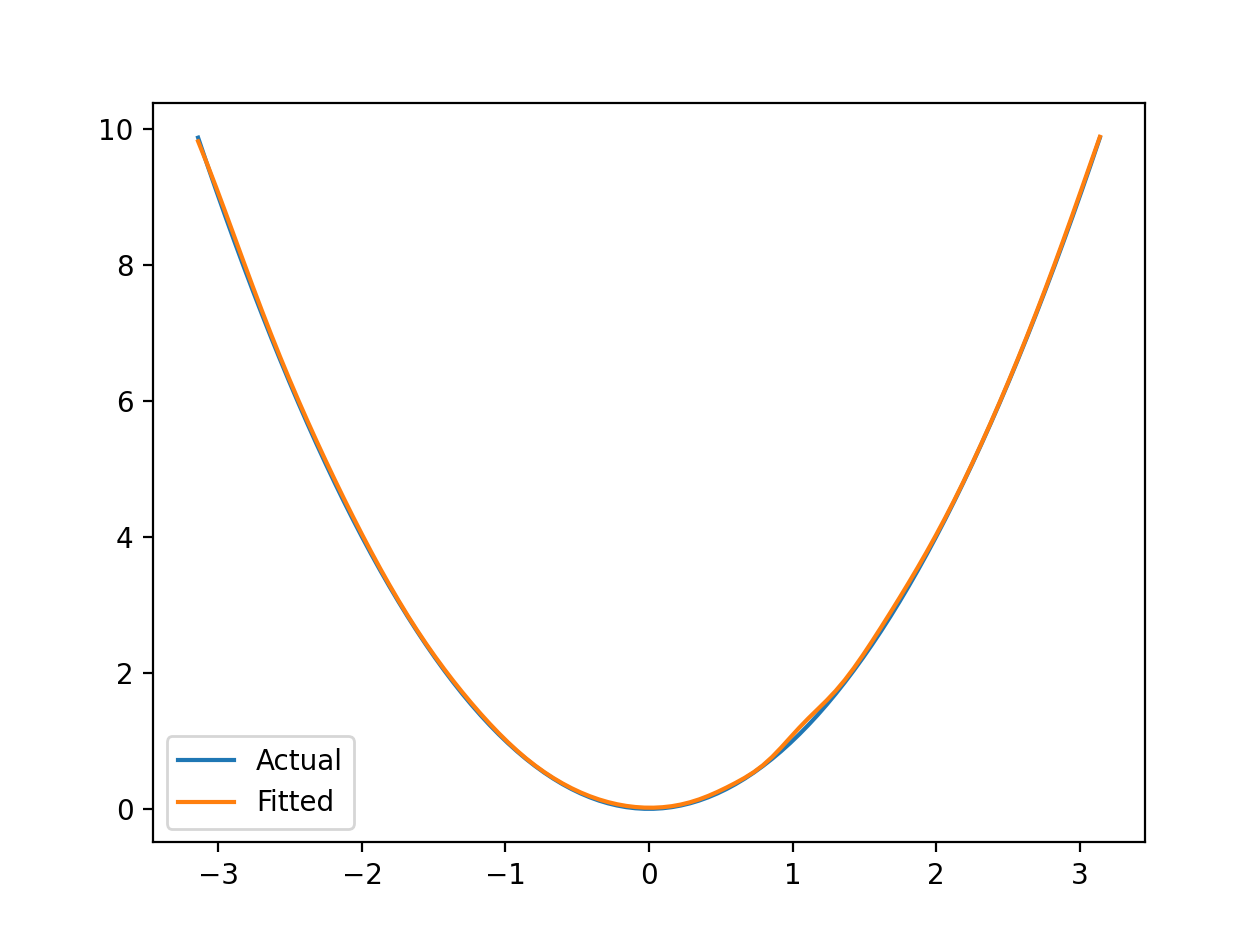
x 2 x^2 x2:
hidden_size:12,epoch:1000,learn_rate:0.1测试集正确率:99.67%,允许误差: ± 0.01 \pm 0.01 ±0.01
-
s i n h ( x ) sinh(x) sinh(x):
hidden_size:12,epoch:1000,learn_rate:0.1测试集正确率:96.53%,允许误差: ± 0.01 \pm 0.01 ±0.01
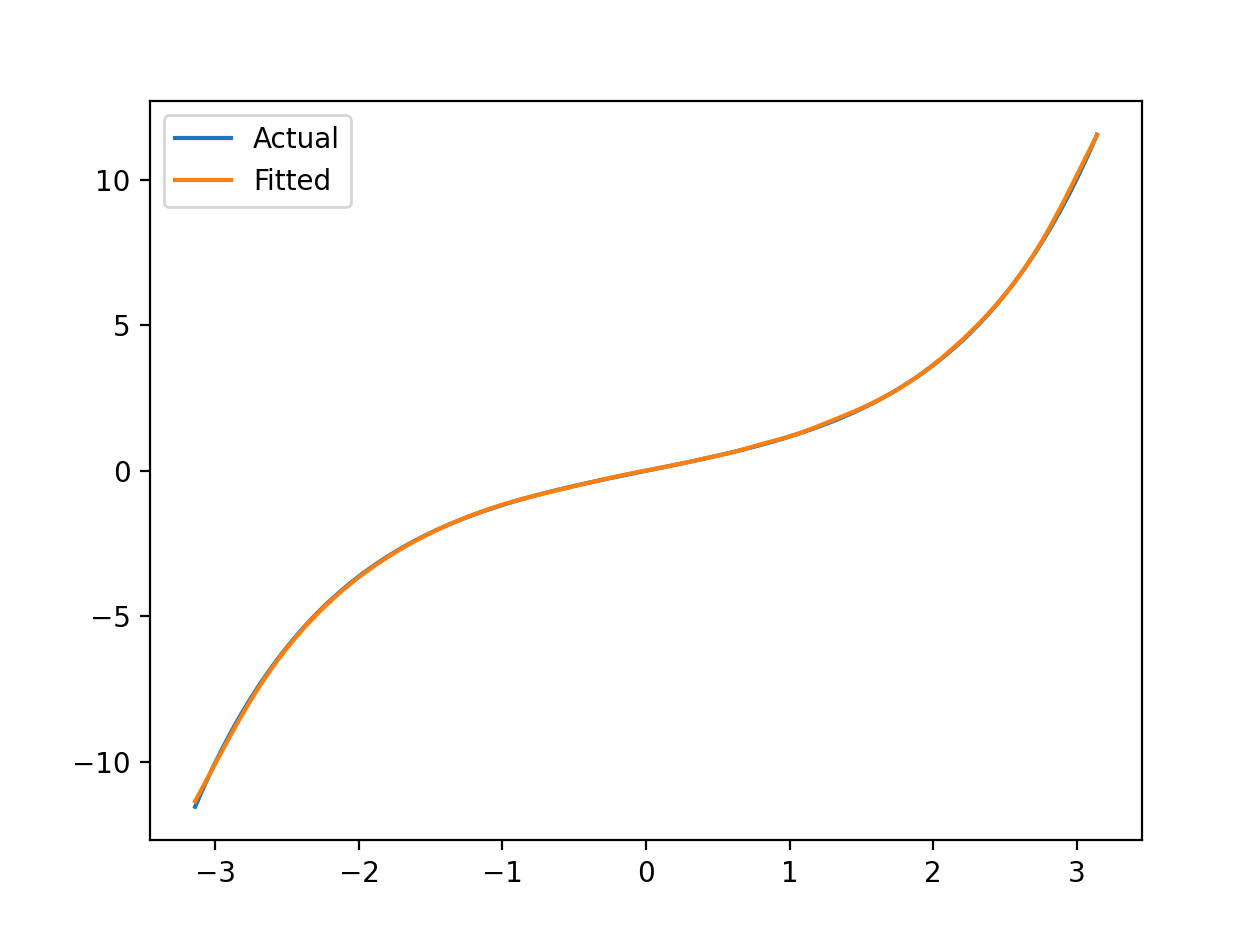
-
e x e^x ex:
hidden_size:12,epoch:1000,learn_rate:0.1测试集正确率:93.33%,允许误差: ± 0.01 \pm 0.01 ±0.01
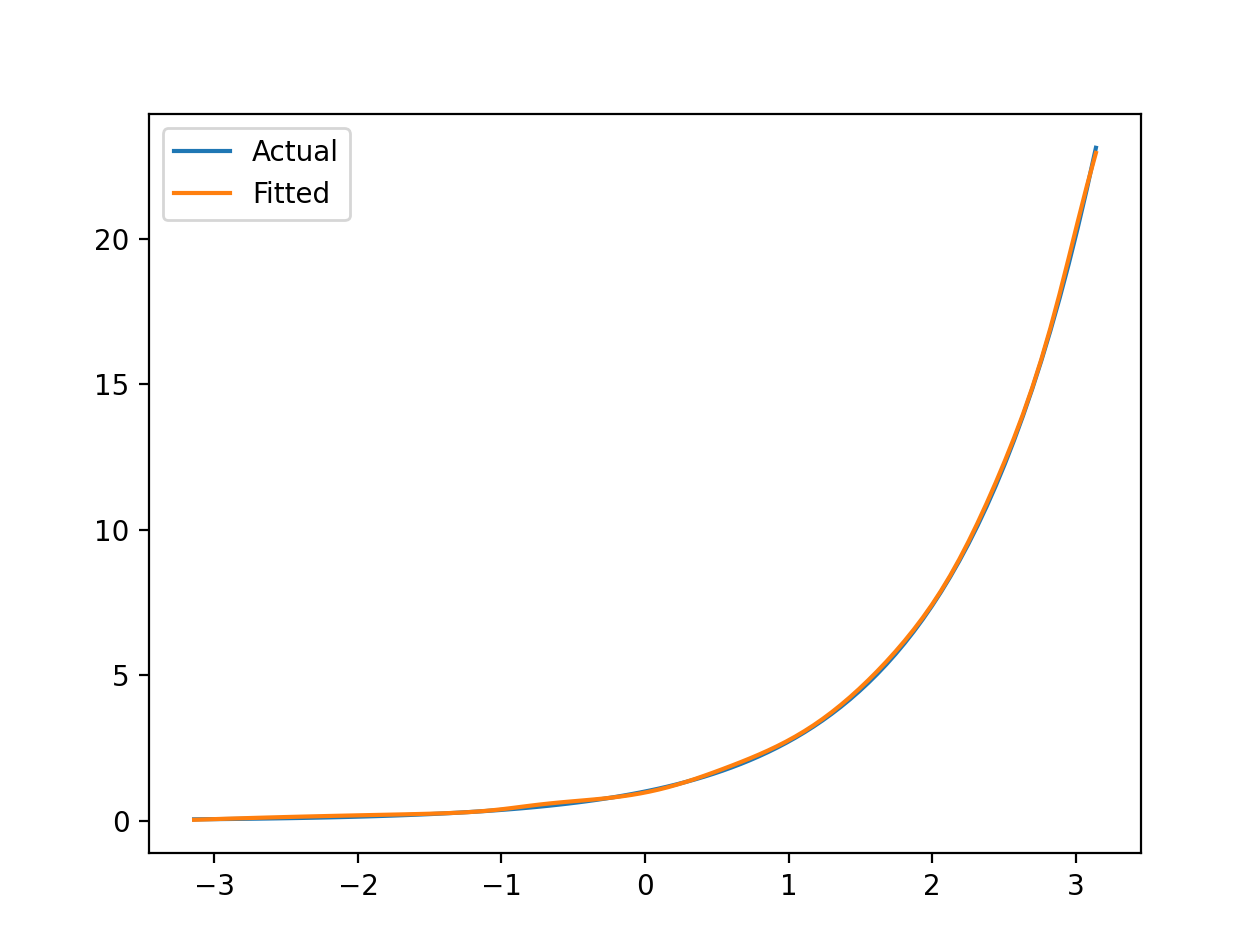
-
x 4 + 2 x 3 − 11 x 2 + 18 x − 6 x^4+2x^3-11x^2+18x-6 x4+2x3−11x2+18x−6:
hidden_size:12,epoch:1000,learn_rate:0.1测试集正确率:2.19%,允许误差: ± 2 \pm 2 ±2
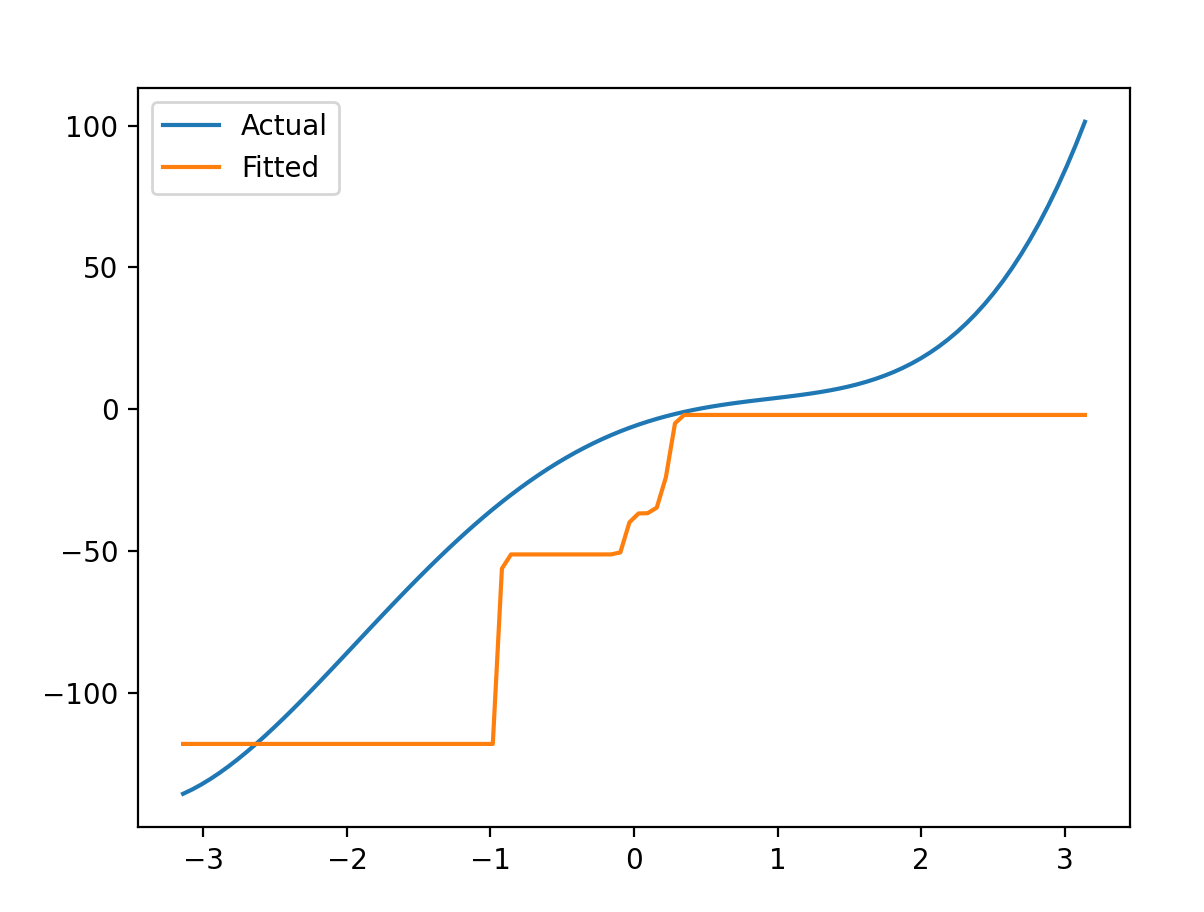
这种是落入了局部最小值,调参的时候应该减小学习率相应调整
epoch。hidden_size:12,epoch:2000,learn_rate:0.01测试集正确率:89.52%,允许误差: ± 2 \pm 2 ±2
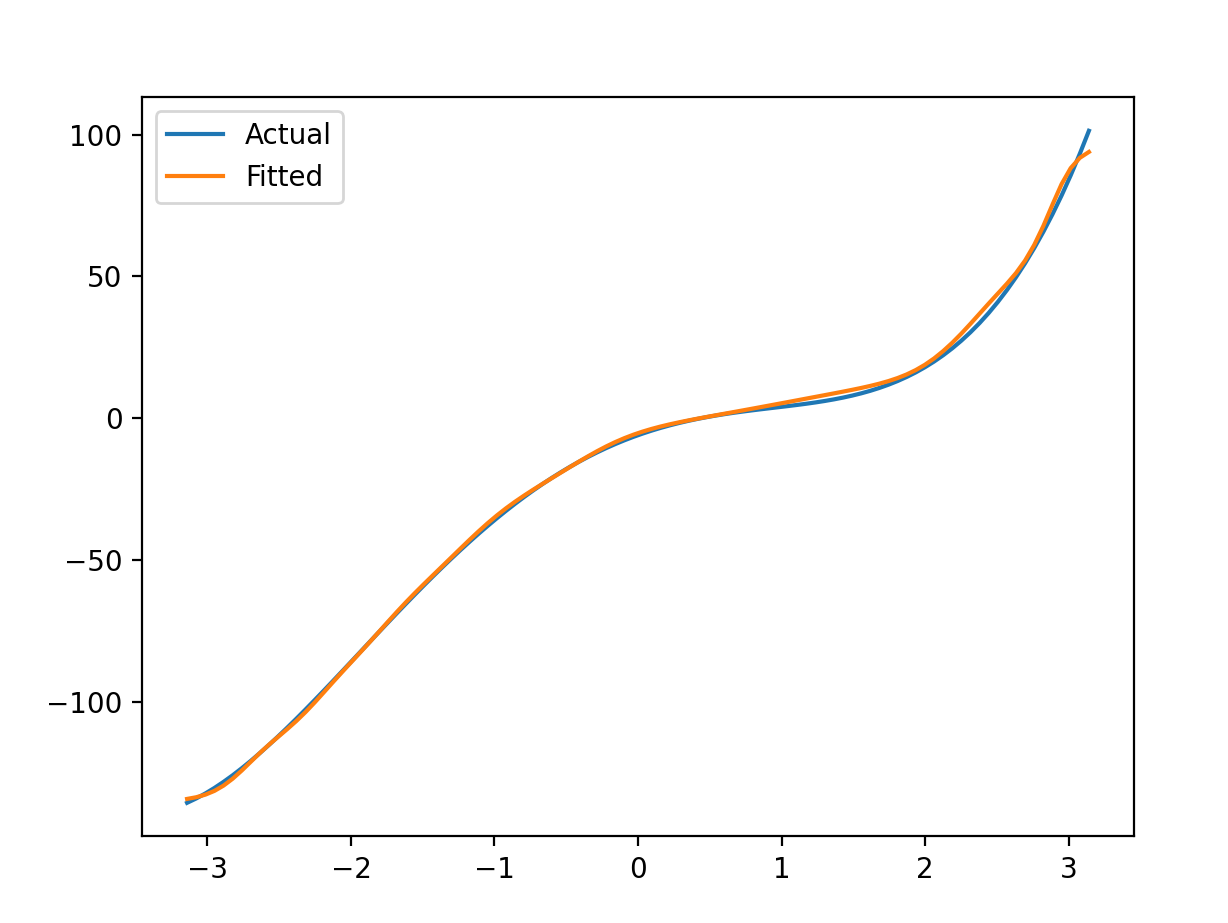























 5284
5284











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










