论文分享：Kolmogorov-Arnold Networks(KANs)

一、从MLP到Kolmogorov-Arnold Networks(KANs)

1.1 背景知识

1.1.1 MLP与KAN的异同

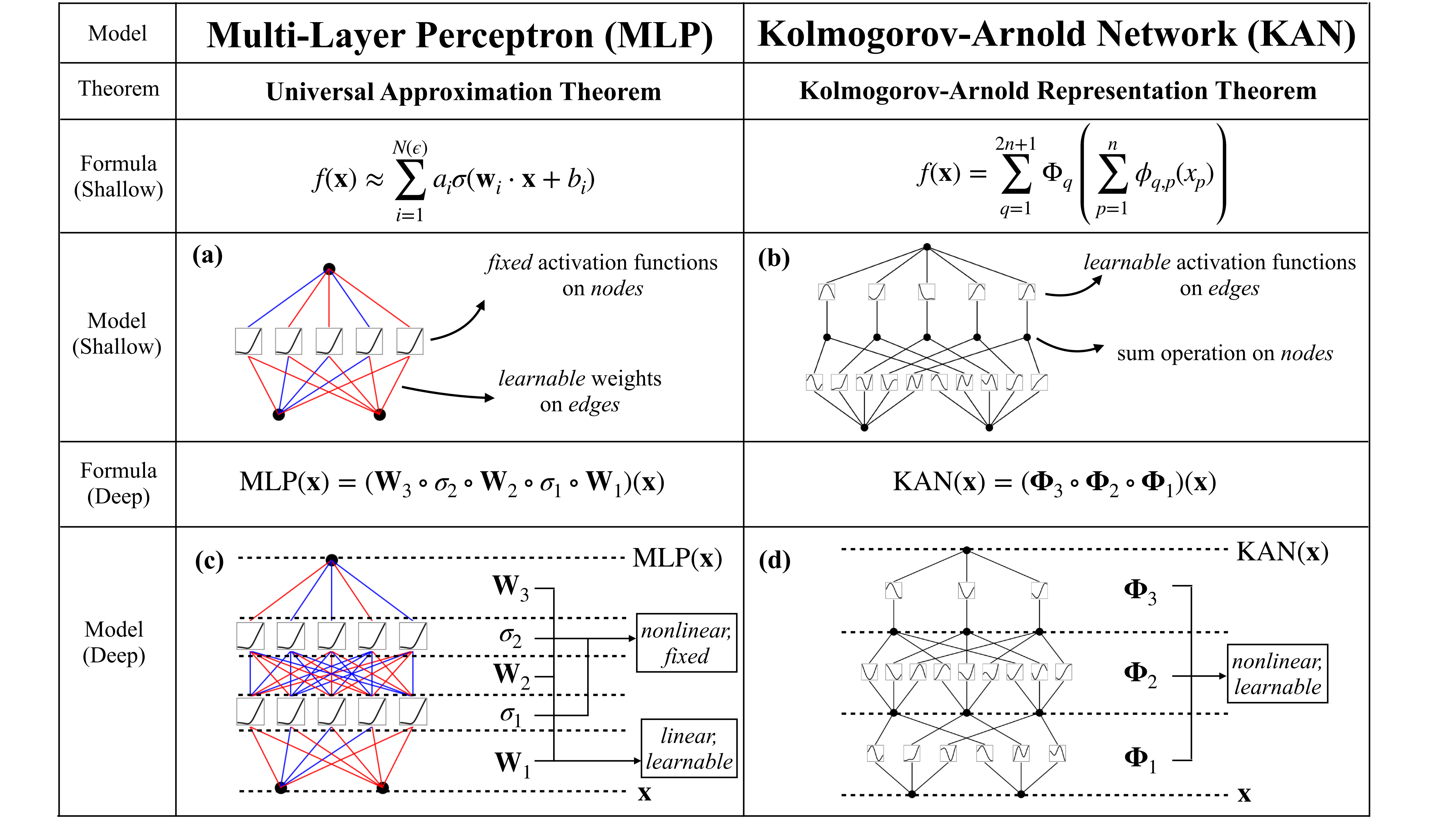
        多层感知器(MLPs)，也被称为全连接前馈神经网络(在节点“神经元”上具有固定的激活函数)，是当今深度学习模型的基础构建模块。

1. 在MLP中，神经元之间的连接通常是一个实数值，代表连接的强度或权重，而神经元本身配有一个非线性的激活函数，如ReLU、sigmoid。所以 MLP的计算过程是：先对权重输入加权，然后通过激活函数引入非线性；

2. 作为机器学习中用于逼近非线性函数的默认模型，其由通用逼近定理来实现。因此，作者团队提出了一个替代方案，称为Kolmogorov-Arnold Networks(KANs)。

           KAN的创新设计是：它没有将权重参数表示为一个实数，而是表示为一种B样条函数(即B-spline，一般都文章都会把spline翻译成样条，即spline = 样条)，这个样条函数直接连接两个神经元，代替了MLP中的线性权重。
           也就是说，KAN的神经元是“无感知”的，它只是把各条连接的函数输出“归拢”起来(简单的求和)。激活函数从节点挪到了边上，就是说，“先变后加”。
           有点类似于，KAN对神经元之间的信息流不再使用固定的“连接件”，而是给每一个连接“管道”装上了可以自由调节的"水龙头"(可学习的“阀门”B样条函数)来控制信息的流动，从而可以随着数据的不同而自动调整形状，让“水流”更加顺畅。

3. 总之，与MLPs类似，KANs具有全连接结构。然而，MLPs在节点——「神经元」上具有固定的激活函数。而KANs在边——「权重」上具有可学习的激活函数。
   如下图所示：
   

       因此，KANs根本没有线性权重矩阵：相反，每个权重参数都被可学习的一维函数取代，参数化为样条函数，且KANs的节点只是简单地对传入信号求和，而不施加任何非线性。
       与MLPs受到通用逼近定理的启发不同，KANs受到Kolmogorov-Arnold表示定理的启发。

1.1.2 Kolmogorov-Arnold表示定理

(任意多变量连续函数可以表示为一系列单变量函数的组合)
Vladimir Arnold(算是前苏联神通)和其导师Andrey Kolmogorov(前苏联科学院院士)证明

       如果$f$是有界域上的多元连续函数，则$f$可以写成有限个连续函数的复合单变量和加法的二元运算。

解释：
       任意一个连续函数$f(x_1,x_2,\cdots ,x_n)$都可以表示为有限个单变量函数的嵌套组合(如下公式所示，其中 ${\varphi }_{q,p}$、${\Phi }_q$都是单变量函数)
$$\begin{gathered} f(\mathbf{x})=f(x_1,\cdots ,x_n)=\sum _{q=1}^{2n+1}{\Phi }_q\left(\sum _{p=1}^n{\varphi }_{q,p}(x_p)\right) \\ {\varphi }_{q,p}:[0,1]\to \mathbb{R}\mathrm{and}{\Phi }_q:\mathbb{R}\to \mathbb{R}. \end{gathered}$$

公式详解

1. $x_p$代表向量$x$的第$p$个元素，故$p$的范围是从1到$n$ ($n$是输入向量的维度)
2. $q$是外部索引，用于遍历外部函数 $\Phi$的每个组成部分
3. ${\varphi }_{q,p}$是一元函数 (或称单变量函数)，用于处理输入向量$x$的第$p$个分量，并为第$q$个外部函数的输入求和贡献一个项
4. 定理指出，可以用 2n+1 个这样的外部函数——每个外部函数${\Phi }_q$是一个一元函数(它作用于由内部一元函数${\varphi }_{q,p}$的输出组成的求和)，来表示任何多变量函数$f$
   :::

       总之，每个函数都可以用一元函数和求和来表示，看似前途一片光明，因为学习高维函数可以因此归结为学习多项式数量的一维函数。
       然而，这些一维函数可能是非光滑甚至是分形的，因此在实践中可能无法学习。一个高维函数可以归结为学习多项式数量级的一维函数，但问题在于，这些一维函数不一定都是好学的光滑函数，它们中的一些不但可能是非光滑的，甚至是极其复杂的，也正因为这种非光滑函数的存在，限制了该定理中实践中的应用价值。即是：理论上正确，但实践中问题诸多。

1.2 样条函数

1.2.1多项式拟合

$f(x)=a{x}^5+b{x}^4+c{x}^3+d{x}^2+ex+f$

1.2.2 贝塞尔曲线（Bezier Curve）

       贝塞尔曲线的作用：贝塞尔曲线的作用是给定控制点，通过控制点生成对应的曲线进行轨迹拟合，输入为点，输出为受到控制点约束而产生的轨迹。

6个控制点5阶贝塞尔函数

1.2.2.1 一阶贝塞尔（bezier）曲线

       如上，$P_0,P_1$两点构成了一条线段，而我们可以通过一个函数——线性插值（lerp），来根据一个$t$值（$t\in [0,1]$） 得到线段上一点$P$（图中一直在滑动的点）。而 $P$ 的运动轨迹（红线），便是一阶贝塞尔线段（曲线）。线性插值的数学形式（一阶贝塞尔曲线公式）为：
$$P=lerp(P_0,P_1,t)=(1-t)P_0+t{P}_1$$
       一阶贝塞尔曲线有两个端点$(P_0,P_1)$，0个控制点。

1.2.2.2 二阶贝塞尔（bezier）曲线

       如上，假设现在有点$P_2$，它与 $P_1$构成了新的线段，我们得到两个一阶插值点$(Q_1,Q_2)$，它们构成了绿色线段，值得注意的是，两个插值点具有相同的$t$值。
       而此时我们在绿色线段上生成一个二阶插值点（$P$），并让它具有 与两个一阶插值点相同的$t$** 值。 那么该点的运动轨迹就是 二阶贝塞尔曲线。其公式推导为：
       绿色线段左端点的运动轨迹：
$$Q_1=(1-t)P_0+t{P}_1$$
       绿色线段右端点的运动轨迹：
$$Q_2=(1-t)P_1+t{P}_2$$
       二阶贝塞尔曲线公式：
$$\begin{array}{rl}P=& (1-t)Q_1+t{Q}_2\\ =& (1-t)((1-t)P_0+t{P}_1)+t((1-t)P_1+t{P}_2)\\ =& (1-t{)}^2{P}_0+2t(t-1)P_1+t^2{P}_2\end{array}$$
       二阶贝塞尔曲线有两个端点** $(P_0,P_2)$，一个控制点$(P_1)$。

1.2.2.3 三阶贝塞尔（bezier）曲线

       经过对一阶、二阶贝塞尔曲线的研究，我们能知道贝塞尔曲线通过在两点之间再采点的方式实现降阶，每一次选点都是一次的降阶。

• $P_0,P_1,P_2,P_3$通过生成插值点 $Q_1,Q_2,Q_3$来构成二阶贝塞尔（绿色线段）
• 在此基础上生成插值点 $O_1,O_2$来构成一阶贝塞尔（蓝色线段）
• 之后以 $O_1$、$O_2$上的插值点 $P$的运动轨迹来生成三阶贝塞尔曲线。

       公式推导过程同二阶贝塞尔曲线，因此不做赘述，公式如下：

$$P=(1-t{)}^3{P}_0+3t(1-t{)}^2{P}_1+3t^2(1-t)P_2+t^3{P}_3$$
       三阶贝塞尔曲线有两个端点$(P_0,P_3)$，两个控制点$(P_1,P_2)$。

1.2.2.4 高阶贝塞尔（bezier）曲线

• 四阶贝塞尔曲线示意图：
  
• 五阶贝塞尔曲线示意图：
  
• 高阶贝塞尔曲线公式：
  $$\begin{gathered} P(t)=\sum _{i=0}^n{P}_i{B}_{i,n}\left(t\right),t\in [0,1] \\ {B}_{i,n}\left(t\right)=C_n^i{t}^i(1-t{)}^{n-i}=\frac{n!}{i!(n-i)!}{t}^i(1-t{)}^{n-i},\text{【}i=0,1,...,n\text{】} \end{gathered}$$

1.2.2.5 应用

       在熟悉了贝塞尔曲线的相关概念之后，介绍它的具体应用。通常它的应用场景是：

       已知两个端点和两个控制点的情况下，根据动画进度向量$P_x$求$t$，再由$t$确认的曲线求$P_y$。

三阶贝塞尔曲线公式：
$$P=(1-t{)}^3{P}_0+3t(1-t{)}^2{P}_1+3t^2(1-t)P_2+t^3{P}_3$$
       公式中的$P_0,P_1$ 等都是二维向量，由两个一维向量$P_x$和$P_y$构成。因此，根据$t$求$P$,本质上是根据$t$来求一个坐标$(x,y)$。因此，可将公式拆解在两个一维向量上：
$$\begin{gathered} x=(1-t{)}^3{P}_{x0}+3t(1-t{)}^2{P}_{x1}+3t^2(1-t)P_{x2}+t^3{P}_{x3} \\ y=(1-t{)}^3{P}_{y0}+3t(1-t{)}^2{P}_{y1}+3t^2(1-t)P_{y2}+t^3{P}_{y3} \end{gathered}$$

1.2.3 从贝塞尔曲线到B样条基函数

1.2.3.1 多段贝塞尔曲线

       对于一个复杂弯曲的曲线，我们希望使用一个贝塞尔曲线来插值获得目标曲线，为此我们可以通过增加控制点来进行插值。但目标曲线越复杂，需要的控制点就越多，而 贝塞尔曲线幂次 = 控制点个数 - 1，即需要的计算也越复杂。该方法虽然可行，但是不明智的，低效率的。另外对于单一的贝塞尔曲线，改变其中一个控制点，那么整条曲线都会随之改变。
       因此对于复杂曲线，一般做法是，使用三次贝塞尔曲线（常用次）一段一段地拼接成目标曲线，正如 Ps 或 Ai 中使用钢笔工具画出物体轮廓所做的那样。 如果使用这种方法，确保最终整体曲线$c^1$连续的条件是：在连接点出两侧的斜率相等，即连接点和其两侧控制点共线。
       例：下图是由两个三次贝塞尔曲线组成的曲线：

       假设，从左到右依次为$P_0,P_1,\cdots ,P_6$，确保两端曲线拼接起来$c^1$连续的条件就是$P_2,P_3,P_4$三点共线。

1.2.3.2 贝塞尔曲线到B样条

       回到最初问题上，通过一系列点，获取一条光滑的曲线。也即通过这些控制点，生成一系列点坐标，这些点坐标形成光滑曲线。
       对于贝塞尔曲线上点的生成，是通过如下方程函数
$$\mathrm{B}(\mathrm{t})=\sum _{\mathrm{i}=0}^{\mathrm{n}}{\mathrm{C}}_{\mathrm{n}}^{\mathrm{i}}(1-\mathrm{t}{)}^{\mathrm{n}-\mathrm{i}}{\mathrm{t}}^{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}},\mathrm{t}\in [0,1]$$
       可展开为
$$\mathrm{B}(\mathrm{t})={\mathrm{W}}_{\mathrm{t},\mathrm{n}}^0{\mathrm{P}}_0+{\mathrm{W}}_{\mathrm{t},\mathrm{n}}^1{\mathrm{P}}_1+\cdots +{\mathrm{W}}_{\mathrm{t},\mathrm{n}}^{\mathrm{n}}{\mathrm{P}}_{\mathrm{n}}$$
       其中$W_{t,n}^0$为$P_0$前系数，是最高幂次为$n$的关于$t$的多项式。当$t$确定后，该值就为定值。因此整个式子可以理解为$B(t)$插值点是这$n+1$点施加各自的权重$W$后累加得到的。这可以解释为什么改变其中一个控制点，整个贝塞尔曲线都会受到影响。
       其实对于样条曲线的生成，思路就是这样的，最终曲线的生成，就对于各个控制点施加权重即可。在贝塞尔曲线中，该权重是关于$t$ 的函数即
$${\mathrm{W}}^{\mathrm{i}}={\mathrm{C}}_{\mathrm{n}}^{\mathrm{i}}(1-\mathrm{t}{)}^{\mathrm{n}-\mathrm{i}}{\mathrm{t}}^{\mathrm{i}}$$
       在B样条中，只不过这个权重设置更复杂点，下面一点点剖析其B样条曲线形成的原理。

1.2.4 B-Spline(B样条曲线）

基本概念：
       1.样条曲线(Spline Curves)： 是给定一系列控制点而得到的一条曲线，曲线形状由这些点控制。一般分为插值样条和拟合样条。
       2.插值：在原有数据点上进行填充生成曲线，曲线必经过原有数据点。
       3.拟合：依据原有数据点，通过参数调整设置，使得生成曲线与原有点差距最小（最小二乘），因此曲线未必会经过原有数据点。

       上面提到，生成曲线，本质上就是在控制点前增加一个权重，然后累加即可。

• 控制点：也就是控制曲线的点，等价于贝塞尔函数的控制点，通过控制点可以控制曲线形状。假设有$n+1$个控制点$P_0,P_1,P_2,\cdots ,P_n$
• 节点：这个跟控制点没有关系，而是人为地将目标曲线分为若干个部分，其目的就是尽量使得各个部分有所影响但也有一定独立性，这也可解释为什么B样条中，有时一个控制点的改变，不会很大影响到整条曲线，而只影响到局部的原因，这是区别于贝塞尔曲线的一点。节点划分影响到权重计算，实现局部性的影响的原理即是在生成某区间内的点时，某些控制点前的权重值会为0，即对该点没有贡献，所以才有上述特点。假设我们划分了$m+1$个节点$t_0,t_1,\cdots ,t_m$，将曲线分成了$m$段
• 次与阶：次的概念就是贝塞尔中次的概念，即权重中$t$的最高幂次。而 阶=次+1。假设我们用 $k$表示次，即$k$次。

1.2.4.1 B-Spline曲线

       对于Bspline曲线的构造我们只需要给定一系列的$n+1$个控制点$p_0,\cdots ,p_n$(control points)以及包含$m+1$个节点的节点向量 U = { u 0 , ⋯   , u m } U=\{u_0,\cdots,u_{m}\} U={u0​,⋯,um​} (knot vector)，以及次数$k$即可进行计算。
       首先，B-Spline曲线的基础计算公式为：
$$C(u)=\sum _{i=0}^n{p}_i{N}_{i,k}\left(u\right)$$
       其中$p_i$是人为选取或者求取的控制点，$N_{i,k}(u)$是$k$次（$k+1$阶）基函数（这里，$k$次的意思是$N_{i,k}(u)$中包含了$u$的$k$次项$u^k$，这里假设$k$从0开始取值）。
       在这一公式的基础上我们只需要确定控制点以及基函数，就可以计算给定$u$时的曲线点位置。后者可以通过Cox-de Boor递归公式来确定：
$$\begin{gathered} N_{i,0}(u)=\{\begin{array}{ll}1& \text{if}{u}_i\le u<u_{i+1}\text{and}{u}_i<u_{i+1}\\ & \\ 0& \text{otherwise}\end{array} \\ {N}_{i,j}\left(u\right)=\frac{u-u_i}{u_{i+j}-u_i}{N}_{i,j-1}\left(u\right)+\frac{u_{i+j+1}-u}{u_{i+j+1}-u_{i+1}}{N}_{i+1,j-1}\left(u\right) \end{gathered}$$

1.2.4.2 次数、控制点数目和节点数目的关系

次数$k$，控制点数目$n+1$和节点数目$m+1$，需要满足
$$m=n+k+1$$

说明：
       如果给出了5个控制点，要求计算次数为3的B样条曲线，我们需要自行设置长度为9的节点向量。这是因为由Cox-de Boor递归公式我们可以知道计算$N_{i,k}(u)$，我们需要计算$N_{i,k-1}(u)和N_{i+1,k-1}(u)$,可以得到计算流图：

从而得到$m=n+k+1$

---

B样条基函数的重要性质
性质一：
       基函数$N_{i,k}(u)$在区间$[u_i,u_{i+k+1})$上非零。即$N_{i,k}(u)$在$k+1$个结点区间$[u_i,u_{i+1}),[u_{i+1},u_{i+2}),\cdots ,[u_{i+k},u_{i+k+1})$上非零。
性质二：
       在任意结点区间$[u_i,u_{i+1})$上，最多有$k+1$个次数为$k$的基函数是非零的，即：
$$N_{i-k,k}\left(u\right),N_{i-k+1,k}\left(u\right),N_{i-k+2,k}\left(u\right),\dots ,N_{i-1,k}\left(u\right)\text{和}{N}_{i,k}\left(u\right)$$

---

举例

控制点5个，节点10个，次数为4次。（满足$m=n+k+1$）

• 目标：获得最终的样条函数。已知一系列控制点，共5个。
• 问题转化为：求每个控制点前的系数，即$W_i$。$W_i$是关于$t$的函数，最高幂次为$k$。在B样条中，通常记为$B_{i,k}(t)$，即表示第$i$个关于$t$的$k$次B样条基函数。注意其是关于变量$t$的函数。

$$\mathrm{B}(\mathrm{t})=\sum _{\mathrm{i}=0}^{\mathrm{n}}{\mathrm{W}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}$$
       只要确定了B样条基函数$B_{i,k}(t)$的取值，就能确定出样条函数和曲线。在例子中，目标是获取5个控制点$P_0,P_1,P_2,P_3,P_4$对应的5个权重值$B_{0,4},B_{1,4},B_{2,4},B_{3,4},B_{4,4}$。

       如上图，目标是获得右侧五个值，表中$b_{i,k}$代表含义与$B_{i,k}$相同，因为不是我们需要的最终值，而是需要求解的中间递推值，所以用小写表示。

---

第一阶段：$k=0$
如果$t\in [t_j,t_{j+1}]$，规定$b_{j,0}=1$，其余$b$均为0。

第二阶段：$k=1$
       $b_{j,1}$取值与低一次的相邻两节点相关，即与 0 次同域两端的节点相关。即$b_{j,1}$求解与$b_{j,0},b_{j+1,0}$相关。求解关系形式为：
$$b_{j,1}=A(t)b_{j,0}+B(t)b_{j+1,0}$$
       这里$A(t),B(t)$是关于$t$的一次幂函数。具体为：
$$\begin{gathered} \mathrm{A}(\mathrm{t})=\frac{\mathrm{t}-{\mathrm{t}}_{\mathrm{j}}}{{\mathrm{t}}_{\mathrm{j}+\mathrm{k}}-{\mathrm{t}}_{\mathrm{j}}} \\ \mathrm{B}(\mathrm{t})=\frac{{\mathrm{t}}_{\mathrm{j}+\mathrm{k}+1}-\mathrm{t}}{{\mathrm{t}}_{\mathrm{j}+\mathrm{k}+1}-{\mathrm{t}}_{\mathrm{j}+1}} \end{gathered}$$
       这里有点类似与贝塞尔函数中递推过程中的前两值的线性组合。
       我们用箭头表示上述计算过程，如下所示：

第三阶段：$k=2$
       此时是关于 t 的二次幂函数，同时$b$数量减少了$2(k=2)$个，还剩$m-k=9-2=7$个。
$\cdots \cdots \cdots \cdots$
第$x$阶段： $k=x$
       非0值会是关于$t$ 的$x$次函数。当执行到第$k$个阶段时，$b$即为关于$t$的$k$次函数。同时$b$减少了$k$个，还剩$m-k$个。

总结：
       执行结束后，得到$n+1=5$个$b$样条基函数，即有等式：
$$m-k=n+1$$
也即$m=n+k+1$。

注：本例中$[t_2,t_3]$区间的曲线上的点不受第四和第五个控制点变化的影响。（说明）

       对于$n+1$个控制点$P_0,P_1,\cdots ,P_n$，有一个包含$m+1$个节点的列表（或节点向量）$t_0,t_1,\cdots ,t_m$，其$k$次B样条曲线表达式为（且$m=n+k+1$）
$$\mathrm{P}\left(\mathrm{t}\right)=\sum _{\mathrm{i}=0}^{\mathrm{n}}{\mathrm{B}}_{\mathrm{i},\mathrm{k}}\left(\mathrm{t}\right){\mathrm{P}}_{\mathrm{i}}$$
       其中$B_{i,k}(t)$称为$k$次B样条基函数，也叫调和函数。且$B_{i,k}(t)$满足如下递推式：
$$\begin{gathered} \mathrm{k}=0,{\mathrm{B}}_{\mathrm{i},0}\left(\mathrm{t}\right)=\{\begin{array}{cc}1,& \mathrm{t}\in [{\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}}+1)\\ 0,& \mathrm{Otherwise}\end{array} \\ \mathrm{k}>0,{\mathrm{B}}_{\mathrm{i},\mathrm{k}}\left(\mathrm{t}\right)=\frac{\mathrm{t}-{\mathrm{t}}_{\mathrm{i}}}{{\mathrm{t}}_{\mathrm{i}+\mathrm{k}}-{\mathrm{t}}_{\mathrm{i}}}{\mathrm{B}}_{\mathrm{i},\mathrm{k}-1}\left(\mathrm{t}\right)+\frac{{\mathrm{t}}_{\mathrm{i}+\mathrm{k}+1}-\mathrm{t}}{{\mathrm{t}}_{\mathrm{i}+\mathrm{k}+1}-{\mathrm{t}}_{\mathrm{i}+1}}{\mathrm{B}}_{\mathrm{i}+1,\mathrm{k}-1}\left(\mathrm{t}\right) \end{gathered}$$

二、KAN的发展起源：从何发展而来以及如何扩宽、扩深

2.1 KAN的提出是为了解决什么问题

       进一步，如果我们面对一个由输入-输出对$(x_i,y_i)$组成的监督学习任务，则

1. 我们需要找到$f$ ，使得对所有数据点都有$y_i\approx f(x_i)$，从而只需找到适当的一元函数${\varphi }_{q,p}$和${\Phi }_q$即可，由此而启发需要设计一个神经网络，以明确地参数化公式2.1（KA定理）。
2. 由于要学习的所有函数都是一元函数，故可以将每个一维函数参数化为B-spline曲线，其中参数是局部 B-spline基函数的可学习系数(见下图右侧)

       对于KAN而言，它

1. 如上所说，不同于传统的MLP，KAN中每一条连接的权重不再是一个简单的数值，而是被参数化为一个可学习的样条函数。这个函数描述了信号从一个节点传递到另一个节点的过程中，是如何被转化和调制的。
2. 通过B样条函数来参数化：${\varphi }_{q,p}$、${\Phi }_q$这些单变量函数，并通过组合这些函数来构建整个网络。

---

       到目前为止，我们有了 KAN 的原型，其计算图完全由方程式(2.1)指定，并在下图(b)中进行了说明。

• 输入维度为 2，呈现为一个两层神经网络。
• 激活函数放置在边edges上而不是节点nodes上(节点上执行简单求和)，中间层的宽度为$2n+1$，相当于将可学习的激活函数从神经元移到了神经网络的边(权重)上。

       总之，在KAN之前，便有不少研究利用Kolmogorov-Arnold表示定理构建神经网络。然而，大多数工作仍停留在原始深度为2、宽度为$2n+1$的表示上「深度为2、宽度为2n+1，即2-Layer KAN with shape [n, 2n + 1, 1]」，并没有机会利用反向传播训练网络。
       KAN的贡献在于将原始Kolmogorov-Arnold表示扩展为任意宽度和深度。

2.2 如何把KAN从2层2n+ 1宽推广到更深、更宽

       在MLPs中，一旦我们定义了一个层(由线性变换和非线性组成)，便可以堆叠更多层使网络更深。类似的，要构建深层KANs，首先要回答：“什么是KAN层？” 原来，具有输入维度和输出维度的KAN层可以被定义为一维函数矩阵（定义为公式2.2）
Φ = { ϕ q , p } , p = 1 , 2 , ⋯   , n i n , q = 1 , 2 ⋯   , n o u t \boldsymbol{\Phi}=\{\phi_{q,p}\} ,\quad p=1,2,\cdots,n_{\mathrm{in}} ,\quad q=1,2\cdots,n_{\mathrm{out}} Φ={ϕq,p​},p=1,2,⋯,nin​,q=1,2⋯,nout​
       其中函数${\varphi }_{q,p}$具有可训练参数。

Kolmogorov-Arnold定理中的KANs层：

1. 内部函数${\varphi }_{q,p}$形成一个KAN层，其中输入维度$n_{in}=n$，输出维度$n_{out}=2n+1$
   (这表明每个输入变量$x_p$通过一组函数转换，输出的数量是输入数量的两倍加一，这样设计是为了充分捕获输入特征的信息并转化为中间表示。)

2. 外部函数${\Phi }_q$形成一个KAN层，其中输入维度$n_{in}=2n+1$，输出维度$n_{out}=1$
   (这层的功能是将内部函数层的所有输出整合起来，形成最终的模型输出)
          因此，方程2.1中的Kolmogorov-Arnold表示简单地由两个KAN层组成：
   $$f(\mathbf{x})=f(x_1,\cdots ,x_n)=\sum _{q=1}^{2n+1}{\Phi }_q\left(\sum _{p=1}^n{\varphi }_{q,p}(x_p)\right)$$

       KAN的形状由整数数组表示：$[n_0,n_1,\cdots ,n_L]$，以下图为例。

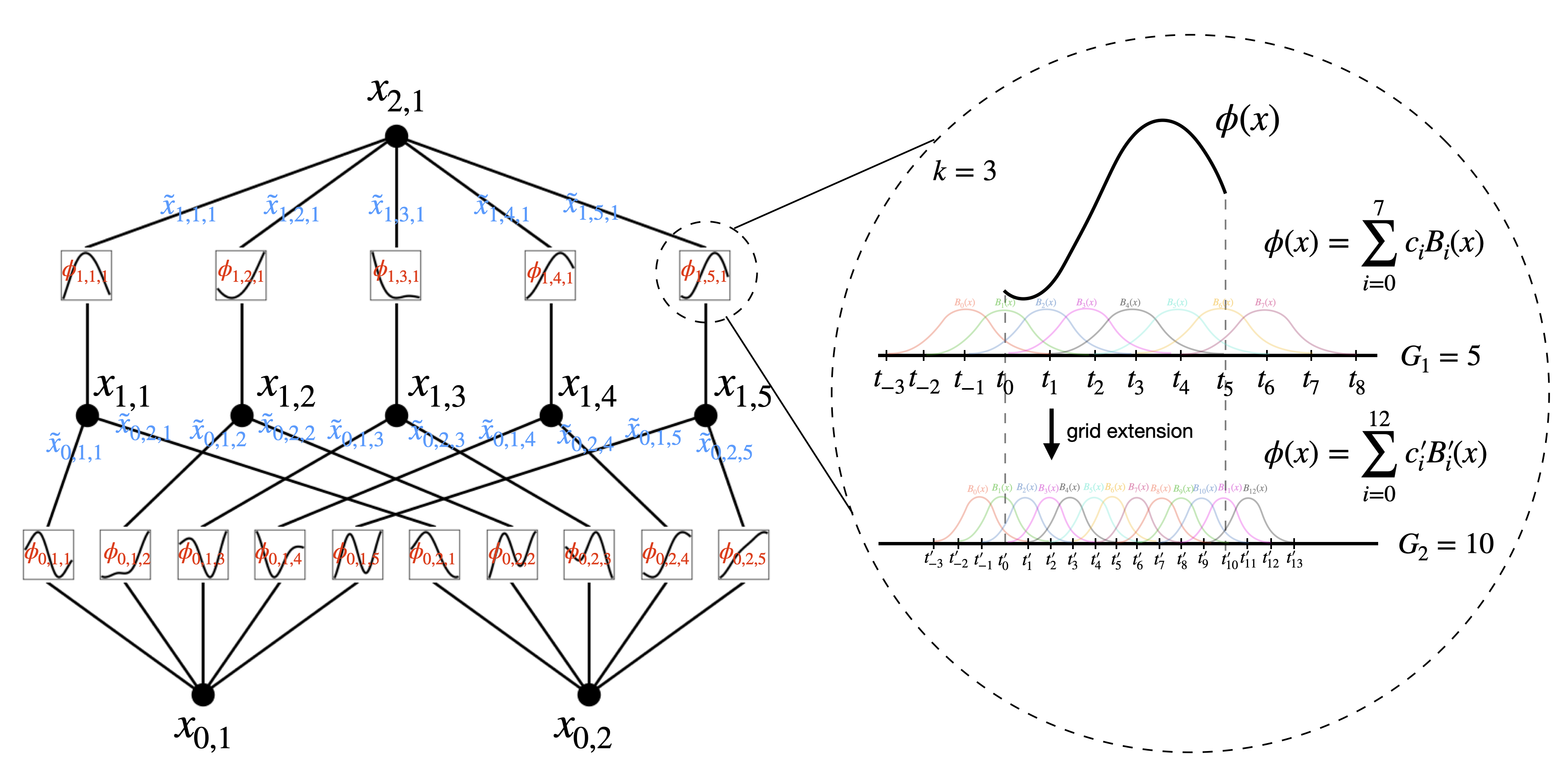
1. 其中$n_i$表示计算图中第$i$层的节点数(比如当从0开始计数的话，上图第1层总计5个节点)。我们用$(l,i)$表示第$l$层的第$i$个神经元，其激活值记为$x_{l,i}$。
2. 在第$l$层和第$l+1$层之间，有$n_l\times n_{l+1}$个激活函数：连接$(l,i)$和$(l+1,j)$的激活函数表示为（$f_{l,i\to l+1,j}$）。

$$\begin{array}{r}{\varphi }_{l,j,i},l=0,\cdots ,L-1,i=1,\cdots ,n_l,j=1,\cdots ,n_{l+1}.\end{array}$$

3. ${\varphi }_{l,j,i}$的预激活值即为$x_{l,i}$；其后激活值表示为${\tilde{x}}_{l,j,i}\equiv {\varphi }_{l,j,i}(x_{l,i})$。$(l+1,j)$神经元的激活值则是所有入向后激活值的简单和：

$$\begin{array}{c}{x}_{l+1,j}=\sum _{i=1}^{n_l}{\tilde{x}}_{l,j,i}=\sum _{i=1}^{n_l}{\varphi }_{l,j,i}(x_{l,i}),j=1,\cdots ,n_{l+1}.\end{array}$$

4. 在矩阵形式中，这可以表示为

$${\mathbf{x}}_{l+1}=\underset{{\Phi }_l}{\underbrace{\left(\begin{array}{cccc}{\varphi }_{l,1,1}(\cdot )& {\varphi }_{l,1,2}(\cdot )& \cdots & {\varphi }_{l,1,n_l}(\cdot )\\ {\varphi }_{l,2,1}(\cdot )& {\varphi }_{l,2,2}(\cdot )& \cdots & {\varphi }_{l,2,n_l}(\cdot )\\ ⋮& ⋮& & ⋮\\ {\varphi }_{l,n_{l+1},1}(\cdot )& {\varphi }_{l,n_{l+1},2}(\cdot )& \cdots & {\varphi }_{l,n_{l+1},n_l}(\cdot )\end{array}\right)}}{\mathbf{x}}_l$$
       其中，${\mathbf{\Phi }}_l$ 是第 $l$ 层 KAN 网络对应的功能矩阵。

5. 一个通用的 KAN 网络由 $L$ 层组成：给定输入向量 $x_0\in {\mathbb{R}}^{n_0}$，KAN 的输出为

$$\mathrm{KAN}(\mathbf{x})=({\mathbf{\Phi }}_{L-1}\circ {\mathbf{\Phi }}_{L-2}\circ \cdots \circ {\mathbf{\Phi }}_1\circ {\mathbf{\Phi }}_0)\mathbf{x}$$

6. 将上述方程重写，假设输出维度$n_L=1$，并定义$f(x)\equiv \text{KAN}(x)$：

$$f(\mathbf{x})=\sum _{i_{L-1}=1}^{n_{L-1}}{\varphi }_{L-1,i_L,i_{L-1}}\left(\sum _{i_{L-2}=1}^{n_{L-2}}\cdots \left(\sum _{i_2=1}^{n_2}{\varphi }_{2,i_3,i_2}\left(\sum _{i_1=1}^{n_1}{\varphi }_{1,i_2,i_1}\left(\sum _{i_0=1}^{n_0}{\varphi }_{0,i_1,i_0}(x_{i_0})\right)\right)\right)\cdots \right)$$

       原始的科洛廖夫-阿诺德表示式对应于一个具有形状$[n,2n+1,1]$的2层KAN。所有操作都是可微分的，因此可以使用反向传播来训练KAN。

三、KAN与MLP的更多异同之处

3.1 MLP如何扩深、扩宽

       为了比较，多层感知器（MLP）可以表示为线性变换矩阵$W$和非线性函数$\sigma$的交替应用：
$$\mathrm{MLP}(\mathbf{x})=({\mathbf{W}}_{L-1}\circ \sigma \circ {\mathbf{W}}_{L-2}\circ \sigma \circ \cdots \circ {\mathbf{W}}_1\circ \sigma \circ {\mathbf{W}}_0)\mathbf{x}$$
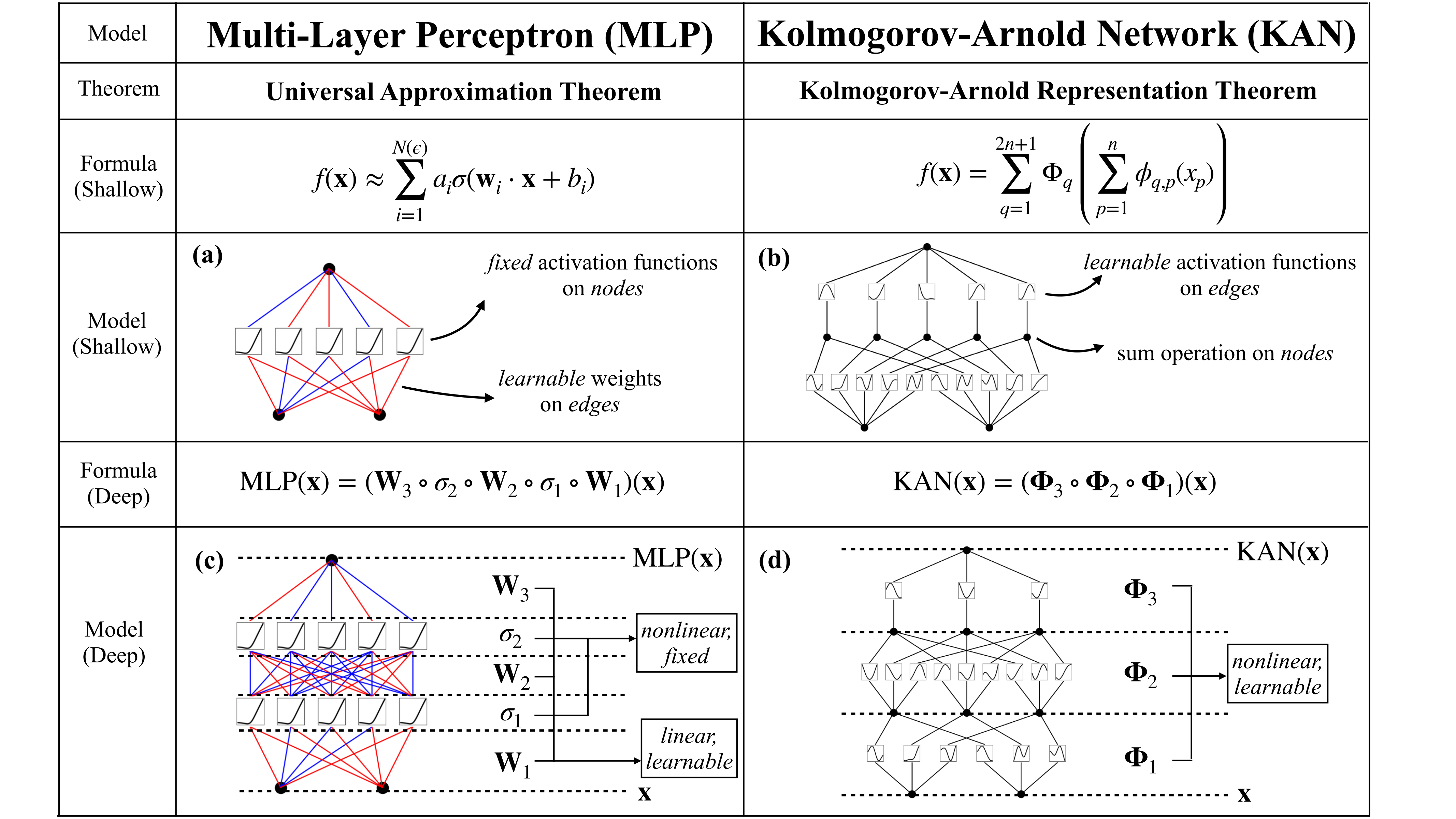
       显然，MLP将线性变换和非线性处理分别视为矩阵$W$和$\sigma$，而KANs则将它们全部整合在矩阵$\Phi$中。如下图©和(d)所示，便是一个一个三层MLP和一个三层KAN。

3.2 KANs = splines(低维函数中准确) + MLPs(可学习组合结构)

       事实上，KANs只不过是splines和MLP的组合，结合了各自的优势，比如:

• splines在低维函数中是准确的，易于局部调整，并能够在不同分辨率之间切换。 然而，splines存在严重的维度问题，无法利用组合结构;
• 另一方面，MLP相对于维度问题的影响较小(归功于它们的特征学习)，但在低维度下比splines不够准确，无法优化单变量函数。

由于KANs

1. 在内部有splines。splines有内部自由度，但没有外部自由度，即splines有内无外（节点之间的连接代表自由度）。还可以将这些学到的特征优化到极高的准确度(与样条的内部相似性)，即可以很好地近似单变量函数；
2. 在外部有MLPs。MLPs有外部自由度，但没内部自由度，MLPs有外无内。

       因此，KANs不仅可以学习特征(与MLPs的外部相似性)，也可以学习多个变量的组合结构。

外部与内部自由度:
       KANs 强调的一个新概念是外部自由度（参数）与内部自由度（参数）之间的区别。节点连接的计算图代表外部自由度（“自由度”），而激活函数内部的网格点是内部自由度。KANs 从拥有外部自由度（MLP 也拥有，但样条不拥有）和内部自由度（样条也拥有，但 MLP 不拥有）中受益。外部自由度负责学习多变量的组合结构，而内部自由度负责学习一元函数。

       例如，给定一个高维函数
$$f\left(x_1,\cdots ,x_N\right)=\exp \left(\frac{1}{N}\sum _{i=1}^N{\sin }^2(x_i)\right)$$
       对于大 $N$，splines会因为COD而失败；MLPs潜在地可以学习广义可加结构，但对于用ReLU激活函数来近似指数和正弦函数非常低效。 相比之下，KANs可以很好地学习组合结构和单变量函数，因此在性能上远远优于MLPs。

3.3 KAN做的一系列优化

3.3.1 残差激活函数

       我们引入一个基函数 $b(x)$（类似于残差连接），使得激活函数 $\varphi (x)$是基函数 $b(x)$和样条函数的和：
$$\begin{array}{r}\varphi (x)=w\left(b(x)+\mathrm{spline}(x)\right)\end{array}$$
       对于前者，设置
$$\begin{array}{r}b(x)=\mathrm{silu}(x)=x/(1+e^{-x})\end{array}$$
       对于后者，在大多数情况下，$\mathrm{spline}(x)$ 参数化为 B 样条函数的线性组合，即（B-spline）
$$\begin{array}{r}\mathrm{spline}(x)=\sum _i{c}_i{B}_i(x)\end{array}$$
       其中$c_i$是可训练的。原则上，$w$是冗余的，因为它可以被吸收进$b(x)$和$spline(x)$中。然而，我们仍然保留这个$w$因子，以便更好地控制激活函数的整体幅度。

3.3.2 初始化规模

       每个激活函数被初始化为 $\mathrm{spline}(x)\approx 0$(这通过抽取小的 $\sigma$ 值, 通常设为 $\sigma =0.1$ 来实现 B-spline 插值系数 $c_i\sim \mathcal{N}(0,{\sigma }^2)$)。$w$ 使用 Xavier 初始化，这是一种常用于多层感知器（MLPs）中线性层的初始化方法。

3.3.3 插值网格的实时更新

       根据输入激活值动态更新每个网格，以解决插值函数定义在有界区域，但训练过程中激活值可能超出固定区域的问题。
       至于其他的可能性解决方法包括:
              a) 通过梯度下降使网格可学习；
              b) 使用归一化保持输入范围。论文曾尝试过 b) 方法，但其性能不如当前的处理方式。

3.3.4 参数数量

为了简化起见，我们假设一个网络（Network, 网络）的参数计数。

• 网络深度为 $L$,
• 每层具有相同的宽度（$n_0=n_1=\cdots =n_L=N$），（其中$L$表示层数，$N$为每层神经元数量）
• 规定样条函数次数为$k$（通常$k=3$）插值（在$G$个区间上），对应$G+1$个网格点。

       然后，总共有$O(N^{2}L(G+k))\sim O(N^{2}LG)$个参数。相比之下，深度为$L$，宽度为$N$的多层感知器（MLP）只需要$O(N^{2}L)$个参数，看起来比KAN更有效率。幸运的是，KAN通常需要的$N$远小于MLP，这不仅节省了参数，而且实现了更好的泛化，并且有利于可解释性。对于一维问题，我们可以取$N=L=1$，KAN网络实际上就是一个样条近似。对于高维情况，我们用逼近定理描述KAN的泛化行为。

3.3.5 MLP和KAN的选择问题

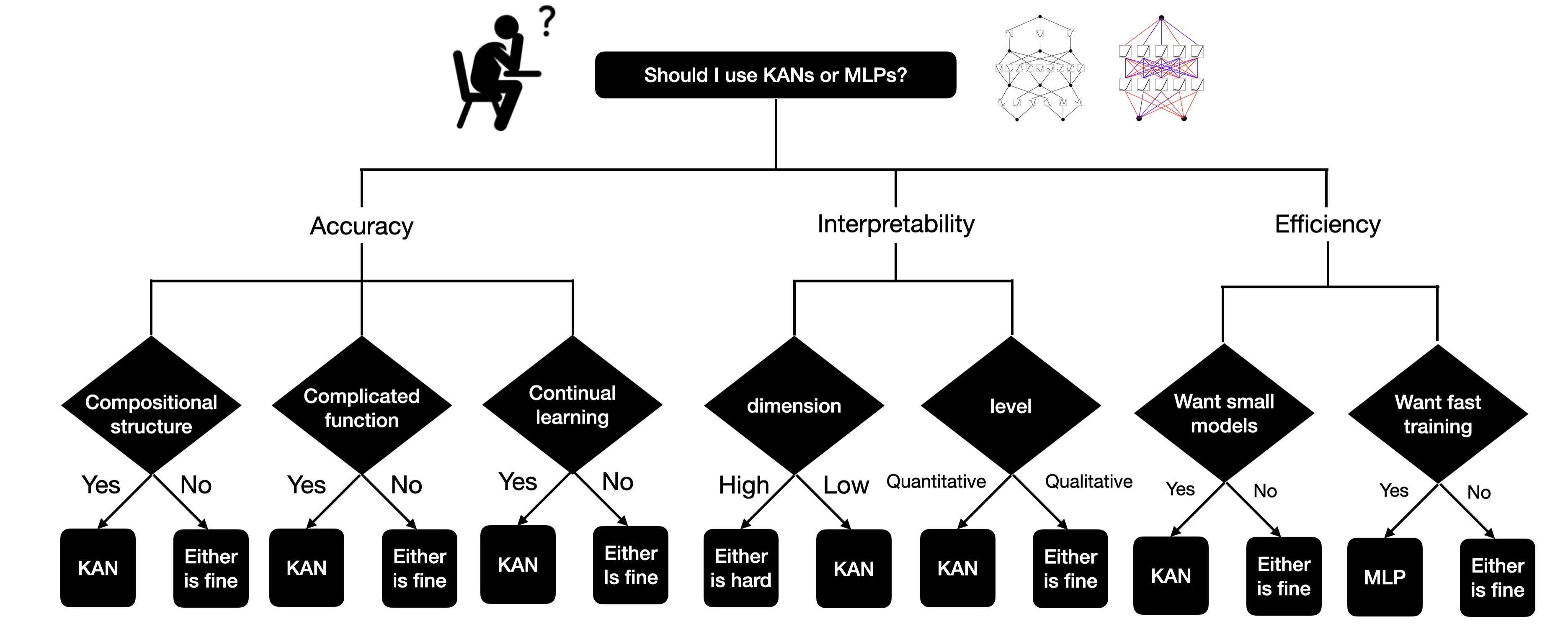
1. 目前，KANs最大的瓶颈在于其训练速度较慢。 在相同数量的参数情况下，KANs通常比MLPs慢10倍。KANs的训练速度较慢更多地是一个需要在未来改进的工程问题，而不是一个基本限制，如果一个人想要快速训练模型，应该使用MLPs；
2. 然而，在其他情况下，KANs应该与MLPs相当或更好，这使得值得尝试，简而言之，如果关心可解释性和/或准确性，并且慢速训练不是一个主要问题，可尝试使用KANs。

四、KAN的逼近能力、准确性、其可解释性

4.1 KAN的逼近能力

4.1.1 分析

       在方程2.1（KA原始方程）中，宽度为$(2n+1)$的2层表示可能是不平滑的。然而，更深的表示可能会带来更平滑的激活函数的优势。例如，4变量函数
$$f\left(x_1,x_2,x_3,x_4\right)=\exp \left(\sin \left(x_1^2+x_2^2\right)+\sin \left(x_3^2+x_4^2\right)\right)$$
       其可以通过一个$[4,2,1,1]$的KAN来平滑表示（层数为3层），但2层KAN便可能没法具备平滑激活性。

为了便于逼近分析

1. 我们考虑允许表示成任意宽和深，以具备激活平滑性，如方程
   $$\mathrm{KAN}(\mathbf{x})=({\mathbf{\Phi }}_{L-1}\circ {\mathbf{\Phi }}_{L-2}\circ \cdots \circ {\mathbf{\Phi }}_1\circ {\mathbf{\Phi }}_0)\mathbf{x}$$
2. 为了强调KAN对有限网格点集的依赖性，使用${\Phi }_l^G$和${\Phi }_{l,i,j}^G$来替代前面方程中的${\Phi }_l$和${\Phi }_{l,i,j}$

从而可得到以下定理：

逼近理论：
       令$x=(x_1,x_2,\cdots ,x_n)$，假设一个函数$f(x)$允许一个表示
$$f=({\Phi }_{L-1}\circ {\Phi }_{L-2}\circ \cdots \circ {\Phi }_1\circ {\Phi }_0)x$$
       其中每个${\Phi }_{l,i,j}$都是$(k+1)$次连续可微的。那么存在一个依赖于$f$及其表示的常数$C$，使得我们有以下关于网格大小$G$的逼近界：存在$k$阶B样条函数${\Phi }_{l,i,j}^G$，对于任意$0\le m\le k$，我们有以下界
$$\Vert f-({\Phi }_{L-1}^G\circ {\Phi }_{L-2}^G\circ \cdots \circ {\Phi }_1^G\circ {\Phi }_0^G)\mathbf{x}{\Vert }_{C^m}\le C{G}^{-k-1+m}$$
       这里我们采用$C^m$-范数来衡量导数到第$m$阶的大小：
$$\Vert g{\Vert }_{C^m}=\underset{|\beta |\le m}{\max }\underset{x\in [0,1{]}^n}{\sup }\left|D^{\beta }g(x)\right|$$

具体解释：

1. 其中的$f$是目标函数(一个多变量函数)，我们希望用KAN来近似它;
2. ${\Phi }_l^G$表示在第$l$层使用的B样条函数，其中$G$表示样条网格的尺寸($G$就是网格的大小，表示每个B样条分段的数量)。随着$G$的变大(意味着使用更大、更细的网格)，spline函数的细节和复杂性增加，从而能够更精确地逼近目标函数$f$;
3. $x$表示输入向量；
4. $||\cdot |{|}_{C^m}$表示$C^m$范数下的误差，用于衡量函数与函数及其导数的最大误差($m$相当于在误差测量中考虑的导数阶数，最高到 $m$ 阶);
5. 不等式右边中的$C$是一个依赖于目标函数$f$及其表示的常数;
6. $k$: B样条的阶数，通常是3(表示三次样条);
7. $-k-1+m$的项展示了B样条的逼近能力，对于光滑函数，当 $m$ 增加时，逼近误差的收敛速度会减慢，但仍保持多项式速率;
8. $G^{-k-1+m}$表示误差界随网格尺寸$G$和spline的阶数$k$而变化;
   换言之，误差的上界随着 $G$ 的增大以$G^{-k-1+m}$的速率下降。

总结：
       描述了随着样条网格细化，KANs模型近似真实函数$f$的精度如何提高，即通过增加网格点的数量($G$越大、网格越大越细)，可以系统地减少近似误差，从而提高模型的预测准确性(意味着需要尽可能选择合适的网格尺寸$G$和spline阶数$k$，以达到所需的近似精度)
       在KA定理成立的情况下，KANs随着网格尺寸的减少可以渐近地很好地逼近函数，并且残差率与维度无关，因此克服了维数灾难。这是因为我们只使用样条来逼近1D函数。
       尽管Kolmogorov-Arnold定理等式对应于一个形状为$[d,2d+1,1]$的KAN表示，但其函数不一定平滑。另一方面，如果能够识别一个平滑的表示（可能以增加层数或使KAN比理论规定的更宽为代价），那么KA定理表明我们可以克服维数灾难（COD）。
       证明了多层的B样条函数可以逼近复杂函数，对于每一层采用不同的intervals，并且这个逼近过程不会出现MLP中存在的维度灾难的影响：即增加网络的深度，不会使得数据的稀疏性和处理的复杂度极度增加。

---

4.1.2 一个说明KAN逼近能力的示例：地形图的绘制

       举例说明下面不等式的含义：
$$\Vert f-({\Phi }_{L-1}^G\circ {\Phi }_{L-2}^G\circ \cdots \circ {\Phi }_1^G\circ {\Phi }_0^G)\mathbf{x}{\Vert }_{C^m}\le C{G}^{-k-1+m}$$
       假设现在有一个任务是绘制一个复杂的地形图。在这个任务中，地形图是由多个不同的高度点组成的，我们希望用一种方法可以尽可能准确地预测任何位置的高度。这里的地形图就像函数 ，而我们想要用KANs来近似这个函数

1. 样条spline网格：Grid Size $G$
          网格可以帮助绘制地形。网格越密集，描绘地形的细节就越多，预测的高度就越精确。这个网格就像spline中的网格尺寸$G$，网格的大小决定了你可以捕获的细节程度。增加$G$(即增加网格点的数量)，就像是用更多的点来绘制地形图，使得最终的图像更接近实际地形;

2. 函数近似误差：$||f-KAN(x)|{|}_{C^m}$
          这表示用KAN模型绘制的地形图与实际地形之间的差异。理想情况下，我们希望这个差异尽可能小，这样我们的地形图就越准确

3. 精度提高的速率$G^{-k-1+m}$
          通过增加网格点的数量，我们可以减少地形图与实际地形之间的差异。具体来说，如果$k$(样条的复杂度或者阶数)、$m$(关注的误差的细节层次，如是否考虑地形的平滑度等)是已知的$(0\le m\le k)$，那么我们可以预测增加网格点的数量将如何提高我们模型的精确度。

---

4.2 神经缩放定律

       讲解了随着参数数量的增加，模型表现能力可以提升，并且对比了几种理论，如何应用他们指导神经网络的设计。

4.3 如何对KAN进行网格扩展(For accuracy: Grid Extension)

4.3.1 将一个新的细粒度样条拟合到一个旧的粗粒度样条上

       原则上，样条可以被制作得足够精确，以逼近目标函数，因为网格可以被制作得足够细粒化。 这一优点被KANs所继承 。

• MLPs没有“细粒化”的概念
         虽然增加MLPs的宽度和深度可以提高性能(神经缩放定律)。 然而，这些神经缩放定律是缓慢的且也很昂贵，因为需要独立训练不同尺寸的模型。

• 对于KANs，可以先训练具有较少参数的KAN，然后通过简单地使其样条网格更细来将其扩展为具有更多参数的KAN，而无需重新从头开始训练较大的模型。

       我们接下来描述如何执行网格扩展（如图右侧所示），这基本上是将一个新的细粒度样条拟合到旧的粗粒度样条上。具体如下：

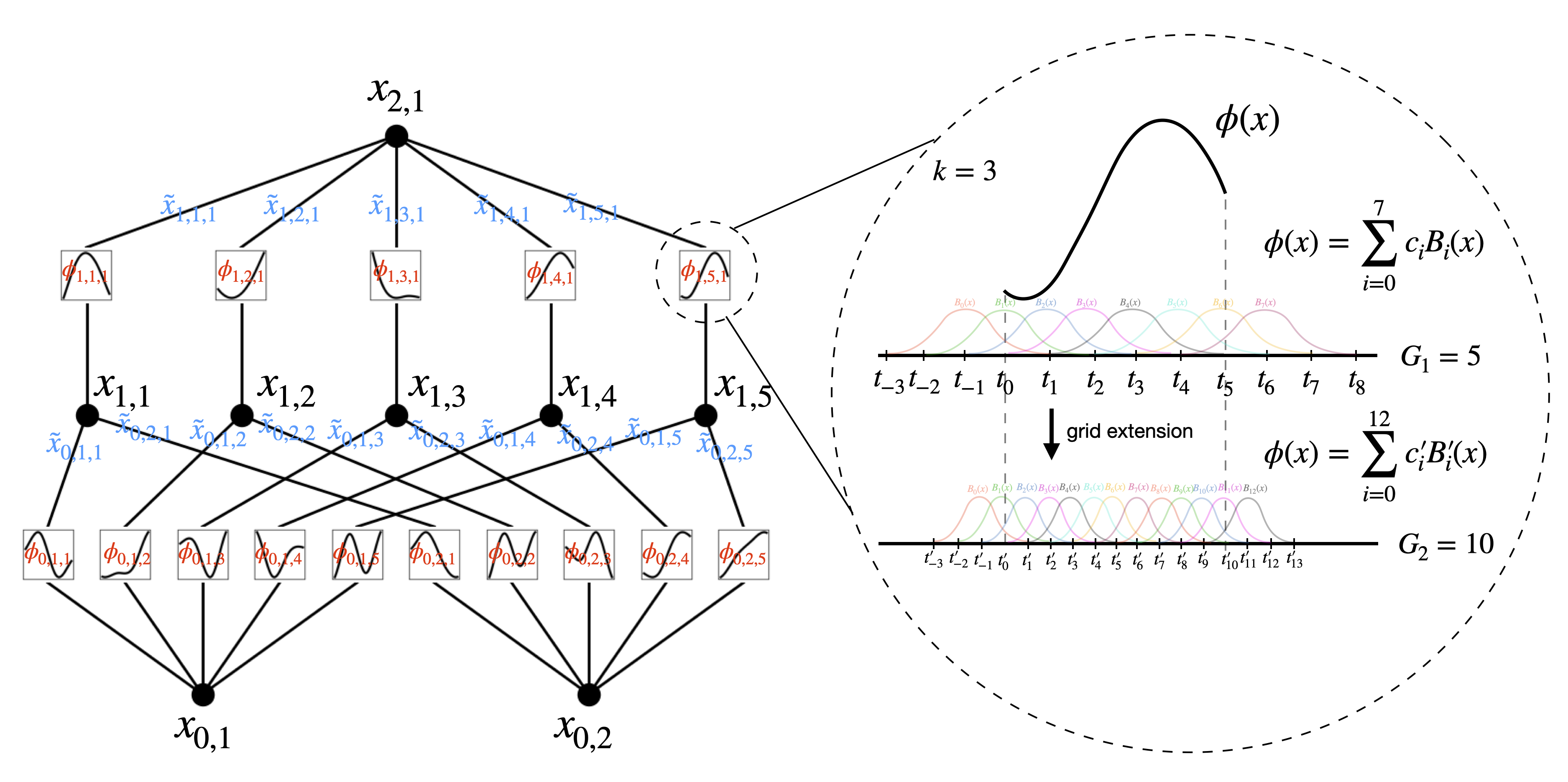
       假设我们想要在一个有界区域$[a,b]$内，用阶数为$k$的B样条来近似一个一维函数$f$。
       一个粗粒度网格有$G_1$个区间，网格点位于 { t 0 = a , t 1 , t 2 , ⋯   , t G 1 = b } \{t_0=a,t_1,t_2,\cdots, t_{G_1}=b\} {t0​=a,t1​,t2​,⋯,tG1​​=b}，扩展到 { t − k , ⋯   , t − 1 , t 0 , ⋯   , t G 1 , t G 1 + 1 , ⋯   , t G 1 + k } \{t_{-k},\cdots,t_{-1},t_0,\cdots, t_{G_1},t_{G_1+1},\cdots,t_{G_1+k}\} {t−k​,⋯,t−1​,t0​,⋯,tG1​​,tG1​+1​,⋯,tG1​+k​}。共有$G_1+k$个B样条基函数，第$i$个B样条$B_i(x)$只在$[t_{-k+i},t_{i+1}]$上非零（$i=0,\cdots ,G_1+k-1$）。
       然后在粗网格上的$f$可以表示为这些B样条基函数的线性组合，即$f_{\text{coarse}}(x)={\sum }_{i=0}^{G_1+k-1}{c}_i{B}_i(x)$。给定一个更细的网格，有$G_2$个区间，细网格上的$f$相应地表示为$f_{\text{fine}}(x)={\sum }_{j=0}^{G_2+k-1}{c}_j^{\prime }{B}_j^{\prime }(x)$。参数$c_j^{\prime }$可以通过最小化$f_{\text{fine}}(x)$与$f_{\text{coarse}}(x)$之间的距离（在某个$x$的分布上）来从参数$c_i$初始化：
{ c j ′ } = argmin { c j ′ }   E x ∼ p ( x ) ( ∑ j = 0 G 2 + k − 1 c j ′ B j ′ ( x ) − ∑ i = 0 G 1 + k − 1 c i B i ( x ) ) 2 \{c_j'\} = \underset{\{c_j'\}}{\text{argmin}}\ \mathop{\mathbb{E}}_{x\sim p(x)}\left(\sum_{j=0}^{G_2+k-1}c_j'B_j'(x)-\sum_{i=0}^{G_1+k-1} c_i B_i(x)\right)^2 {cj′​}={cj′​}argmin​ Ex∼p(x)​(j=0∑G2​+k−1​cj′​Bj′​(x)−i=0∑G1​+k−1​ci​Bi​(x))2
       这可以通过最小二乘算法来实现。我们对KAN中的所有样条独立执行网格扩展。

4.3.2 网格扩展的示例

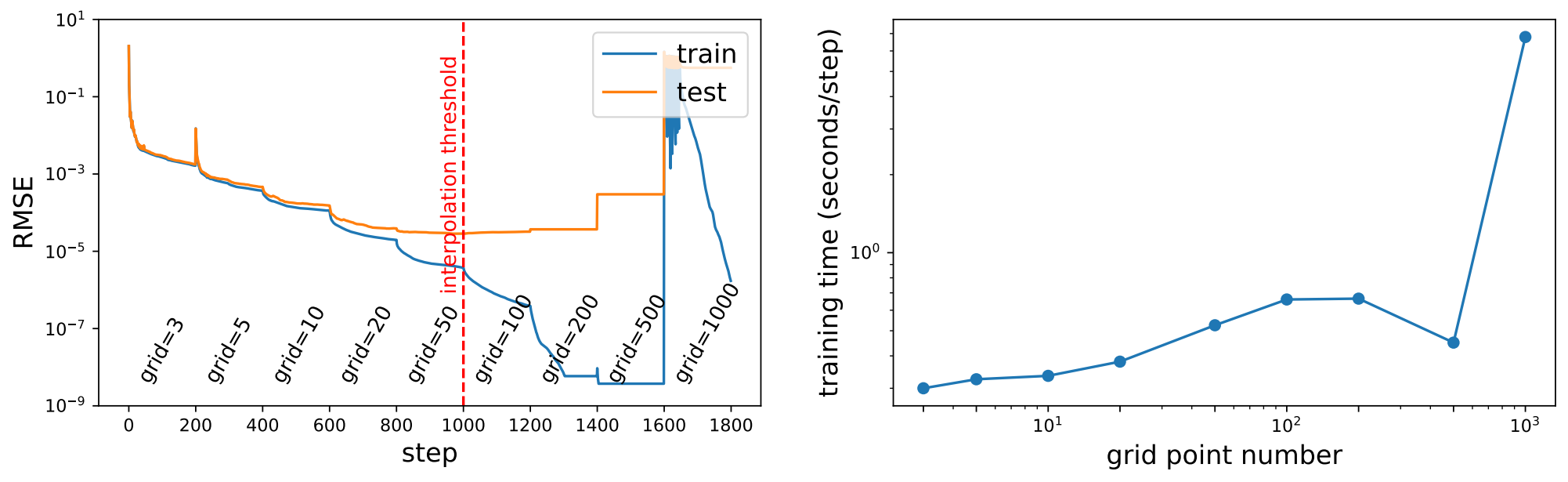
       如上图所示，展示了一个 $[2,5,1]$KAN的训练和测试RMSE。
网格点的数量从3开始，每200个LBFGS步骤增加到更高的值，最终达到1000个网格点。
       很明显，每次进行精细化处理时，训练损失下降速度比以前快(除了具有1000个点的最细网格,由于糟糕的loss landscapes，优化停止工作)。然而，测试损失先下降然后上升，显示出U形状，这是由于偏差-方差权衡(欠拟合与过拟合)造成的。
       作者推测，当参数数量与数据点数量匹配时，最佳测试损失是在插值阈值处实现的。
       比如由于训练样本有1000个，而一个$[2,5,1]$KAN的总参数为$15\times G$($G$是网格间隔的数量)，作者预计插值阈值为$G=1000/15\approx 67$，这与作者实验观察到的值 G ∼ 50大致吻合。

4.4 KAN的可解释性：简化KANs并使其与更好用

4.4.1 自动确定KAN形状的方法

       如何选择与数据集结构最匹配的KAN形状。例如，如果我们知道数据集是通过公式 $f(x,y)=\exp (\sin (\pi x)+y^2)$ 生成的，那么我们知道一个 $[2,1,1]$ 的KAN能够表达这个函数。然而，在实践中我们无法预先知道这些信息，因此需要一些方法来自动确定这个形状。我们的想法是从足够大的KAN开始，通过稀疏正则化训练后进行剪枝。这些剪枝后的KAN比未剪枝的KAN更具可解释性。

4.4.2 简化技术

1. 稀疏化。
          对于MLPs，使用线性权重的L1正则化来促进稀疏性。KAN可以借鉴这个高级思想，但需要进行两个修改：

• KAN中没有线性“权重”。线性权重被可学习的激活函数所取代，因此我们应该定义这些激活函数的L1范数。
• L1对于KAN的稀疏化是不够的；相反，还需要额外的熵正则化。
         我们定义激活函数 $\varphi$ 的L1范数为在其 $N_p$ 个输入上的平均绝对值，即
  $${\left|\varphi \right|}_1\equiv \frac{1}{N_p}\sum _{s=1}^{N_p}\left|\varphi (x^{(s)})\right|$$
         然后，对于一个具有$n_{\mathrm{in}}$个输入和$n_{\mathrm{out}}$个输出的KAN层$\Phi$，我们定义$\Phi$的L1范数为所有激活函数的L1范数之和，即
  $${\left|\Phi \right|}_1\equiv \sum _{i=1}^{n_{\mathrm{in}}}\sum _{j=1}^{n_{\mathrm{out}}}{\left|{\varphi }_{i,j}\right|}_1$$
         此外，我们定义$\Phi$的熵为
  $$S(\mathbf{\Phi })\equiv -\sum _{i=1}^{n_{\mathrm{in}}}\sum _{j=1}^{n_{\mathrm{out}}}\frac{|{\varphi }_{i,j}{|}_1}{|\mathbf{\Phi }{|}_1}\log \left(\frac{|{\varphi }_{i,j}{|}_1}{|\mathbf{\Phi }{|}_1}\right)$$
         总的训练目标${\ell }_{\mathrm{total}}$是预测损失${\ell }_{\mathrm{pred}}$加上所有KAN层的L1和熵正则化：
  $${\ell }_{\mathrm{total}}={\ell }_{\mathrm{pred}}+\lambda \left({\mu }_1\sum _{l=0}^{L-1}{\left|{\Phi }_l\right|}_1+{\mu }_2\sum _{l=0}^{L-1}S({\Phi }_l)\right),$$
         其中${\mu }_1,{\mu }_2$是相对幅度，通常设置为${\mu }_1={\mu }_2=1$，$\lambda$ 控制整体正则化幅度。

2. Visualization
          当我们可视化一个KAN时，为了得到大小的感觉，我们将激活函数 ${\varphi }_{l,i,j}$ 的透明度设置为与 $\tanh (\beta A_{l,i,j})$ 成正比，其中 $\beta =3$ 。因此，大小较小的函数会显得模糊，以便我们能够专注于重要的函数。

3. Pruning
          在使用稀疏化惩罚进行训练后，我们可能还希望将网络剪枝到一个较小的子网络。我们对KANs进行节点级别的稀疏化（而不是边级别的稀疏化）。对于每个节点（比如第 $l$ 层的第 $i$ 个神经元），我们定义其传入和传出分数为
   $$I_{l,i}=\underset{k}{\max }({\left|{\varphi }_{l-1,k,i}\right|}_1),O_{l,i}=\underset{j}{\max }({\left|{\varphi }_{l+1,j,i}\right|}_1)$$
          如果传入和传出分数都大于阈值超参数$\theta =10^{-2}$（默认值），则认为该节点是重要的。所有不重要的神经元都被剪枝。

4. Symbolification.
          在我们怀疑某些激活函数实际上是符号形式（例如，$\cos$ 或 $\log$）的情况下，我们提供了一个接口来将它们设置为指定的符号形式，$\text{fix\_symbolic(l,i,j,f)}$ 可以将 $(l,i,j)$ 激活设置为 $f$。然而，我们不能简单地将激活函数设置为确切的符号公式，因为其输入和输出可能存在偏移和缩放。因此，我们从样本中获取预激活 $x$ 和后激活 $y$，并拟合仿射参数 $(a,b,c,d)$ 使得$y\approx cf(ax+b)+d.$拟合是通过迭代网格搜索$a,b$ 和线性回归来完成的。

4.4.3 一个简单示例：人类如何与KAN互动

       在上面，我们提出了针对网络（KANs）的一系列简化技术。我们可以将这些简化选择视为可以点击的按钮。与这些按钮互动的用户可以决定点击哪个按钮最有希望使KANs更具可解释性。我们下面使用一个示例来展示用户如何与KAN互动以获得最大程度可解释的结果。
再次考虑回归任务

$$f(x,y)=\exp \left(\sin (\pi x)+y^2\right)$$
       给定数据点$(x_i,y_i,f_i)$，$i=1,2,\cdots ,N_p$，假设用户Alice有兴趣找出符号公式。Alice与KANs互动的步骤如下（如上图所示）：

• 步骤 1：使用稀疏化进行训练。从全连接的$[2,5,1]$ KAN开始，使用稀疏化正则化进行训练可以使网络变得相当稀疏。隐藏层中的5个神经元中有4个看起来是无用的，因此我们想要剪枝它们。
• 步骤 2：剪枝。自动剪枝会丢弃所有隐藏神经元，只留下最后一个，得到一个$[2,1,1]$ KAN。激活函数看起来是已知的符号函数。
• 步骤 3：设置符号函数。假设用户可以通过观察KAN图正确猜测这些符号公式，他们可以设置。

       如果用户没有领域知识或者不知道这些激活函数可能是哪些符号函数，我们提供了一个函数$\text{suggest\_symbolic}$来建议符号候选。

• 步骤 4：进一步训练。
         符号化网络中的所有激活函数后，剩下的唯一参数是仿射参数。我们继续训练这些仿射参数，当我们看到损失降至机器精度时，我们知道我们已经找到了正确的符号表达式。
• 步骤 5：输出符号公式。使用Sympy计算输出节点的符号公式。用户       得到$1.0e^{1.0y^2+1.0\sin (3.14x)}$，这是正确答案（我们只显示了$\pi$的两个小数位）。

备注：为什么不使用符号回归（SR）？
       对于这个示例，使用符号回归是合理的。然而，符号回归方法通常是脆弱的并且难以调试。它们最终要么返回成功要么返回失败，而不会输出可解释的中间结果。相比之下，KAN在函数空间中进行连续搜索（使用梯度下降），因此它们的结果更加连续，因此也更加健壮。此外，与SR相比，用户对KAN有更多的控制权，因为KAN具有透明性。我们展示KAN的方式就像向用户展示KAN的“大脑”，用户可以对KAN进行“手术”（调试）。

五、代码

class KANLinear(torch.nn.Module):
    def __init__(
            self,
            in_features,
            out_features,
            grid_size=5,
            spline_order=3,
            scale_noise=0.1,
            scale_base=1.0,
            scale_spline=1.0,
            enable_standalone_scale_spline=True,
            base_activation=torch.nn.SiLU,
            grid_eps=0.02,
            grid_range=[-1, 1],
    ):
        super(KANLinear, self).__init__()
        self.in_features = in_features  # 输入特征数
        self.out_features = out_features  # 输出特征数
        self.grid_size = grid_size  # 网格大小, 网格区间的数量(而不是点的数量)
        self.spline_order = spline_order  # 样条阶数, 即B样条基函数的次数

        '''
        网格的作用:
            (1) 定义B样条基函数的位置：
                B样条基函数是在特定的支持点(控制点)上进行计算的，这些支持点(控制点)由网格确定。
                B样条基函数在这些网格点上具有特定的值和形状。
            (2) 确定样条基函数的间隔：
                网格步长（h）决定了网格点之间的距离，从而影响样条基函数的平滑程度和覆盖范围。
                网格越密集，样条基函数的分辨率越高，可以更精细地拟合数据。
            (3) 构建用于插值和拟合的基础：
                B样条基函数利用这些网格点进行插值，能够构建出连续的、平滑的函数。
                通过这些基函数，可以实现输入特征的复杂非线性变换。
        '''

        # NOTE 计算网格步长，并生成网格
        h = (grid_range[1] - grid_range[0]) / grid_size
        grid = (
            (
                    torch.arange(-spline_order, grid_size + spline_order + 1) * h
                    + grid_range[0]
            )
            .expand(in_features, -1)
            .contiguous()
        )
        # (in_features, grid_size + 2 * spline_order + 1)

        '''
        shape:
            网格: [in_features, grid_size + 2 * spline_order + 1]
            节点向量： [grid_size + 2 * spline_order + 1, ]
            m = n + k + 1
            m + 1 个节点, n + 1 个控制点(对应于 n + 1 个B样条基函数), k次
            m + 1 = (n + 1) + k + 1
            grid_size + 2 * spline_order + 1 = (n + 1) + spline_order + 1
            n + 1 = grid_size + spline_order   B样条基函数个数
        '''
        '''
        .expand(in_features, -1) 的作用:
            将网格点的数量从 grid_size + 2 * spline_order + 1 扩展到 in_features 个。
            这样，每个输入特征都可以使用相同的网格点进行插值。
        '''
        # .expand(in_features, -1): 扩展张量的形状。in_features 是输入特征的数量，-1 表示保持最后一个维度不变
        # .contiguous(): 确保张量在内存中是连续的
        self.register_buffer("grid", grid)  # 注册网格作为模型的buffer
        # PyTorch中，buffer是一种特殊类型的张量，它在模型中起到辅助作用，但不会作为模型参数进行更新。buffer通常用于存储一些在前向和后向传播过程中需要用到的常量或中间结果。buffer和模型参数一样，会被包含在模型的状态字典中（state dictionary），可以与模型一起保存和加载。

        '''
        register_buffer 的作用:
            self.register_buffer("grid", grid) 的作用是将 grid 注册为模型的一个buffer。这样做有以下几个好处：
            (1) 将 grid 注册为模型中的buffer，以便在模型保存和加载时将其包含在内。持久化：buffer会被包含在模型的状态字典中，可以通过 state_dict 方法保存模型时一并保存，加载模型时也会一并恢复。这对于训练和推理阶段都很有用，确保所有相关的常量都能正确加载。
            (2) 无需梯度更新：uffer不会被优化器更新。buffer不会在反向传播过程中计算梯度和更新。它们是固定的，只在前向传播中使用。这对于像网格点这样的常量非常适合，因为这些点在训练过程中是固定的，不需要更新。
            (3) 易于使用：注册为buffer的张量可以像模型参数一样方便地访问和使用，而不必担心它们会被优化器错误地更新。
        '''

        # NOTE 初始化网络参数和超参数

        # TODO 初始化基础(函数)权重参数，形状为 (out_features, in_features)
        self.base_weight = torch.nn.Parameter(torch.Tensor(out_features, in_features))

        # TODO 初始化样条(函数)权重参数，形状为 (out_features, in_features, grid_size + spline_order)
        self.spline_weight = torch.nn.Parameter(
            torch.Tensor(out_features, in_features, grid_size + spline_order)
        )

        # TODO 如果启用了独立缩放样条功能，初始化样条缩放参数，形状为 (out_features, in_features)
        if enable_standalone_scale_spline:
            self.spline_scaler = torch.nn.Parameter(
                torch.Tensor(out_features, in_features)
            )

        # TODO 噪声缩放系数，用于初始化样条(函数)权重时添加噪声
        self.scale_noise = scale_noise

        # TODO 基础(函数)权重的缩放系数，用于初始化基础权重时的缩放因子
        self.scale_base = scale_base

        # TODO 样条(函数)权重的缩放系数，用于初始化样条权重时的缩放因子
        self.scale_spline = scale_spline

        # TODO 是否启用独立的样条缩放功能
        self.enable_standalone_scale_spline = enable_standalone_scale_spline

        # TODO 基础激活函数实例，用于对输入进行非线性变换
        self.base_activation = base_activation()

        # TODO 网格更新时的小偏移量，用于在更新网格时引入微小变化，避免过拟合
        self.grid_eps = grid_eps

        self.reset_parameters()

    def reset_parameters(self):
        # 使用kaiming_uniform_方法初始化基础权重参数base_weight
        # 这个方法基于何凯明初始化，适用于具有ReLU等非线性激活函数的网络
        # a=math.sqrt(5) * self.scale_base 是计算初始化参数的增益（gain）因子
        # self.scale_base 用于调整初始化权重的大小
        torch.nn.init.kaiming_uniform_(self.base_weight, a=math.sqrt(5) * self.scale_base)

        # TODO 这表示接下来的操作不会计算梯度，通常用于一些仅涉及权重初始化或模型评估的操作，以减少计算资源消耗
        with torch.no_grad():
            # SECTION 为样条(函数)权重参数spline_weight添加噪声进行初始化
            '''
            noise = (torch.rand(self.grid_size + 1, self.in_features, self.out_features) - 1 / 2) * self.scale_noise / self.grid_size：
            生成一个随机噪声矩阵，用于初始化样条权重。torch.rand 生成一个元素值在[0,1)区间内均匀分布的随机矩阵，然后减去0.5使元素值的范围变为[-0.5, 0.5)。
            self.grid_size + 1 表示样条函数的节点数量，self.in_features 和 self.out_features 分别表示输入和输出特征的数量。
            self.scale_noise 用于调整噪声大小的参数，self.grid_size 用于对噪声进行归一化。
            '''
            noise = (
                    (
                            torch.rand(self.grid_size + 1, self.in_features, self.out_features)
                            - 1 / 2
                    )
                    * self.scale_noise
                    / self.grid_size
            )
            # noise shape: (grid_size + 1, in_features, out_features)

            # SECTION 计算样条权重参数的初始值，结合了scale_spline的缩放因子
            self.spline_weight.data.copy_(
                (self.scale_spline if not self.enable_standalone_scale_spline else 1.0)
                * self.curve2coeff(
                    self.grid.T[self.spline_order: -self.spline_order],  # (grid_size + 1, in_features)
                    noise,  # (grid_size + 1, in_features, out_features)
                )
            )
            # output: (out_features, in_features, grid_size + spline_order)

            if self.enable_standalone_scale_spline:
                # torch.nn.init.constant_(self.spline_scaler, self.scale_spline)
                # 作者此前使用了一般的初始化，效果不佳
                # 使用kaiming_uniform_方法初始化样条缩放参数spline_scaler
                # spline_scaler shape: (out_features, in_features)
                torch.nn.init.kaiming_uniform_(self.spline_scaler, a=math.sqrt(5) * self.scale_spline)

    def b_splines(self, x: torch.Tensor):
        """
        计算给定输入张量的B样条基函数。
        B样条（B-splines）是一种用于函数逼近和插值的基函数。
        它们具有局部性、平滑性和数值稳定性等优点，广泛应用于计算机图形学、数据拟合和机器学习中。
        在这段代码中，B样条基函数用于在输入张量上进行非线性变换，以提高模型的表达能力。
        在KAN（Kolmogorov-Arnold Networks）模型中，B样条基函数用于将输入特征映射到高维空间中，以便在该空间中进行线性变换。
        具体来说，B样条基函数能够在给定的网格点上对输入数据进行插值和逼近，从而实现复杂的非线性变换。

        参数:
            x (torch.Tensor): 输入张量，形状为 (batch_size, in_features)。

        返回:
            torch.Tensor: B样条基函数张量，形状为 (batch_size, in_features, grid_size + spline_order)。
        """
        # 确保输入张量的维度是2，并且其列数等于输入特征数
        assert x.dim() == 2 and x.size(1) == self.in_features

        # 获取网格点（包含在buffer中的self.grid）  grid的格式为torch.Tensor
        grid = (
            self.grid
        )  # (in_features, grid_size + 2 * spline_order + 1)

        # 为了进行逐元素操作，将输入张量的最后一维扩展一维
        x = x.unsqueeze(-1)  # (batch_size, in_features, 1)

        # 初始化B样条基函数的基矩阵
        # (batch_size, in_features, grid_size + 2 * spline_order)
        bases = ((x >= grid[:, :-1]) & (x < grid[:, 1:])).to(x.dtype)

        # 迭代计算样条基函数
        '''
        grid_node_num == grid_size + 2 * spline_order + 1
        grid_node_num - spline_order - 1 = grid_size + spline_order
        The number of B-spline bases = grid_size + spline_order
        '''
        for k in range(1, self.spline_order + 1):
            bases = (
                            (x - grid[:, : -(k + 1)])
                            / (grid[:, k:-1] - grid[:, : -(k + 1)])
                            * bases[:, :, :-1]
                    ) + (
                            (grid[:, k + 1:] - x)
                            / (grid[:, k + 1:] - grid[:, 1:(-k)])
                            * bases[:, :, 1:]
                    )

        # 确保B样条基函数的输出形状正确
        assert bases.size() == (
            x.size(0),  # (batch_size, in_features, 1)
            self.in_features,
            self.grid_size + self.spline_order,
        )

        # (batch_size, in_features, grid_size + spline_order)
        '''
        输出: (batch_size, in_features, grid_size + spline_order)
        其中，(batch_size, in_features) 是输入张量的形状，
        grid_size + spline_order 是B样条基函数的数量。
        推理: The number of B-spline bases = grid_size + spline_order
        '''
        return bases.contiguous()

    def curve2coeff(self, x: torch.Tensor, y: torch.Tensor):
        """
        计算插值给定点的曲线的系数。
        curve2coeff 方法用于计算插值给定点的曲线的系数。
        这些系数用于表示插值曲线在特定点的形状和位置。
        具体来说，该方法通过求解线性方程组来找到B样条基函数在给定点上的插值系数。
        此方法的作用是根据输入和输出点计算B样条基函数的系数，
        使得这些基函数能够精确插值给定的输入输出点对。
        这样可以用于拟合数据或在模型中应用非线性变换。
        
        参数:
            x (torch.Tensor): 输入张量，形状为 (batch_size, in_features)。
            y (torch.Tensor): 输出张量，形状为 (batch_size, in_features, out_features)。

        返回:
            torch.Tensor: 系数张量，形状为 (out_features, in_features, grid_size + spline_order)。
        """
        # 确保输入张量的维度是2，并且其列数等于输入特征数
        assert x.dim() == 2 and x.size(1) == self.in_features

        # 确保输出张量的形状正确
        assert y.size() == (x.size(0), self.in_features, self.out_features)

        # 计算B样条基函数
        # NOTE .transpose(0, 1): 这个方法调用是对返回的张量进行转置操作。在PyTorch中，transpose(0, 1) 会交换张量的第0维和第1维。这通常用于调整数据的形状，以符合特定操作的要求
        A = self.b_splines(x).transpose(0, 1)  # (in_features, batch_size, grid_size + spline_order)

        # 转置输出张量
        B = y.transpose(0, 1)  # (in_features, batch_size, out_features)

        # 使用线性代数方法求解线性方程组，找到系数
        solution = torch.linalg.lstsq(A, B).solution  # (in_features, grid_size + spline_order, out_features)

        # 调整结果的形状
        result = solution.permute(2, 0, 1)  # (out_features, in_features, grid_size + spline_order)

        # 确保结果张量的形状正确
        assert result.size() == (
            self.out_features,
            self.in_features,
            self.grid_size + self.spline_order,
        )

        # 返回连续存储的结果张量
        return result.contiguous()

    @property
    def scaled_spline_weight(self):
        """
        计算带有缩放因子的样条权重。

        样条缩放：如果启用了 enable_standalone_scale_spline，
        则将 spline_scaler 张量扩展一维后与 spline_weight 相乘，
        否则直接返回 spline_weight。

        具体来说，spline_weight 是一个三维张量，形状为 (out_features, in_features, grid_size + spline_order)。
        而 spline_scaler 是一个二维张量，形状为 (out_features, in_features)。
        为了使 spline_scaler 能够与 spline_weight 逐元素相乘，
        需要将 spline_scaler 的最后一维扩展，以匹配 spline_weight 的第三维。

        返回:
            torch.Tensor: 带有缩放因子的样条权重张量。
        """
        return self.spline_weight * (
            self.spline_scaler.unsqueeze(-1)
            if self.enable_standalone_scale_spline
            else 1.0
        )

    def forward(self, x: torch.Tensor):
        """
        实现模型的前向传播。

        参数:
            x (torch.Tensor): 输入张量，形状为 (batch_size, in_features)。

        返回:
            torch.Tensor: 输出张量，形状为 (batch_size, out_features)。
        """
        # 确保输入张量的最后一维大小等于输入特征数
        assert x.size(-1) == self.in_features

        # 保存输入张量的原始形状
        original_shape = x.shape

        # 将输入张量展平为二维
        '''
        x.view(-1, self.in_features): 这个方法调用是对张量 x 进行重塑操作。
        view 方法用于改变张量的形状而不改变其数据。
            -1: 这个参数表示自动计算这一维的大小，以便所有元素都被包含在新形状中。
            self.in_features: 这是一个属性，表示输入特征的数量。
        '''
        x = x.view(-1, self.in_features)

        # SECTION 计算基础线性变换的输出
        '''
        self.base_activation(x): 这个方法调用表示对输入数据 x 应用一个激活函数。self.base_activation 是一个方法，它接受输入 x 并返回激活后的结果。
        F.linear(...): 这是PyTorch中的一个函数，用于执行线性变换。它将输入数据与权重矩阵相乘，并加上偏置。
        self.base_weight: 这是一个属性，表示该层的权重。
        self.base_activation(x) shape: (batch_size, in_features)
        self.base_weight shape: (out_features, in_features)
        '''
        base_output = F.linear(self.base_activation(x), self.base_weight)
        '''
        F.linear 函数是 PyTorch 中用于执行线性变换的函数。它的参数需要满足特定的维度要求：
            1.输入张量 (x): 这个张量的形状应该是 [batch_size, in_features]。其中，batch_size 是批次大小，in_features 是输入特征的数量。
            2.权重张量 (weight): 这个张量的形状应该是 [out_features, in_features]。其中，out_features 是输出特征的数量，in_features 是输入特征的数量，它应该与输入张量的第二维相匹配。
            3.偏置张量 (bias): 这个张量的形状应该是 [out_features]。
        在使用 F.linear 时，如果你只提供了权重和输入张量，PyTorch 会自动使用一个全零的偏置张量。如果你提供了偏置张量，它的形状应该与输出特征的数量相匹配。
        例如，如果你有一个输入张量 x 形状为 [batch_size, in_features] 和一个权重张量 weight 形状为 [out_features, in_features]，那么 F.linear(x, weight) 将执行以下操作：
        output = x · W^T + bias
        其中，W^T 是权重矩阵 weight 的转置。
        output shape: (batch_size, out_features)
        其中，x 是输入张量，weight 是权重矩阵，bias 是偏置向量。
        '''

        # SECTION 计算B样条基函数的输出
        spline_output = F.linear(
            self.b_splines(x).view(x.size(0), -1),                      # (batch_size, in_features * (grid_size + spline_order))
            self.scaled_spline_weight.view(self.out_features, -1),      # (out_features, in_features * (grid_size + spline_order))
        )
        '''
        shape:
            x:  (batch_size, in_features)
            self.b_splines(x): (batch_size, in_features, grid_size + spline_order)
            注:
                grid_size + spline_order 是B样条基函数的数量。
                推理: The number of B-spline bases = grid_size + spline_order
            self.b_splines(x).view(x.size(0), -1): (batch_size, in_features * (grid_size + spline_order))
            self.scaled_spline_weight: (out_features, in_features, grid_size + spline_order)
            self.scaled_spline_weight.view(self.out_features, -1): (out_features, in_features * (grid_size + spline_order))
            output: (batch_size, out_features)
        '''

        # SECTION 合并基础线性变换和B样条基函数输出
        '''
        base_output shape: (batch_size, out_features)
        spline_output shape: (batch_size, out_features)
        output shape: (batch_size, out_features)
        '''
        # 合并基础输出和样条输出
        output = base_output + spline_output

        # 恢复输出张量的形状
        output = output.view(*original_shape[:-1], self.out_features)

        # (batch_size, out_features)
        return output

    @torch.no_grad()
    def update_grid(self, x: torch.Tensor, margin=0.01):
        """
        update_grid 方法用于根据输入数据动态更新B样条的网格点，从而适应输入数据的分布。
        该方法通过重新计算和调整网格点，确保B样条基函数能够更好地拟合数据。
        这在训练过程中可能会提高模型的精度和稳定性。

        参数:
            x (torch.Tensor): 输入张量，形状为 (batch_size, in_features)。
            margin (float): 网格更新的边缘大小，用于在更新网格时引入微小变化。
        """
        # 确保输入张量的维度正确
        assert x.dim() == 2 and x.size(1) == self.in_features
        batch = x.size(0)  # 获取批量大小

        # 计算输入张量的B样条基函数
        splines = self.b_splines(x)  # (batch, in, coeff)
        splines = splines.permute(1, 0, 2)  # 转置为 (in, batch, coeff)

        # 获取当前的样条权重
        orig_coeff = self.scaled_spline_weight  # (out, in, coeff)
        orig_coeff = orig_coeff.permute(1, 2, 0)  # 转置为 (in, coeff, out)

        # 计算未缩减的样条输出
        unreduced_spline_output = torch.bmm(splines, orig_coeff)  # (in, batch, out)
        unreduced_spline_output = unreduced_spline_output.permute(1, 0, 2)  # 转置为 (batch, in, out)

        # 为了收集数据分布，对每个通道分别进行排序
        x_sorted = torch.sort(x, dim=0)[0]
        grid_adaptive = x_sorted[
            torch.linspace(
                0, batch - 1, self.grid_size + 1, dtype=torch.int64, device=x.device
            )
        ]

        # 计算均匀步长，并生成均匀网格
        uniform_step = (x_sorted[-1] - x_sorted[0] + 2 * margin) / self.grid_size
        grid_uniform = (
                torch.arange(
                    self.grid_size + 1, dtype=torch.float32, device=x.device
                ).unsqueeze(1)
                * uniform_step
                + x_sorted[0]
                - margin
        )

        # 混合均匀网格和自适应网格
        grid = self.grid_eps * grid_uniform + (1 - self.grid_eps) * grid_adaptive
        # output grid shape: (grid_size + 1, in_features)

        # 扩展网格以包括样条边界
        grid = torch.concatenate(
            [
                grid[:1]
                - uniform_step
                * torch.arange(self.spline_order, 0, -1, device=x.device).unsqueeze(1),
                grid,
                grid[-1:]
                + uniform_step
                * torch.arange(1, self.spline_order + 1, device=x.device).unsqueeze(1),
            ],
            dim=0,
        )
        # self.grid shape: (grid_size + 2 * spline_order + 1, in_features)

        # 更新模型中的网格点
        self.grid.copy_(grid.T)    # (in_features, grid_size + 2 * spline_order + 1)

        # 重新计算样条权重
        self.spline_weight.data.copy_(self.curve2coeff(x, unreduced_spline_output))

    def regularization_loss(self, regularize_activation=1.0, regularize_entropy=1.0):
        """
        计算正则化损失。

        这是对论文中提到的原始L1正则化的一种简单模拟，因为原始方法需要从
        展开的 (batch, in_features, out_features) 中间张量计算绝对值和熵，
        但如果我们想要一个高效的内存实现，这些张量会被隐藏在F.linear函数后面。

        现在的L1正则化计算为样条权重的平均绝对值。
        作者的实现还包括这个项，此外还有基于样本的正则化。
        """
        # 计算样条权重的绝对值的平均值
        # spline_weight: (out_features, in_features, grid_size + spline_order)
        l1_fake = self.spline_weight.abs().mean(-1)

        # 计算激活正则化损失，即所有样条权重绝对值的和
        regularization_loss_activation = l1_fake.sum()

        # 计算每个权重占总和的比例
        p = l1_fake / regularization_loss_activation

        # 计算熵正则化损失，即上述比例的负熵
        regularization_loss_entropy = -torch.sum(p * p.log())

        # 返回总的正则化损失，包含激活正则化和熵正则化
        return (
                regularize_activation * regularization_loss_activation
                + regularize_entropy * regularization_loss_entropy
        )