KAN
这是个非常厉害的设计,看完论文我再写评价。
下面是实验,都是作者给出的代码
>>> from kan.KANLayer import KANLayer
>>> model = KANLayer(in_dim=3, out_dim=5)
>>> (model.in_dim, model.out_dim)
(3, 5)
>>> import torch
>>> x = torch.normal(0,1,size=(100,3))
>>> y, preacts, postacts, postspline = model(x)
>>> x = torch.normal(0,1,size=(4, 784, 1024))
>>> x = x.reshape(4*784, 1024)
>>> y, preacts, postacts, postspline = model2(x)
killed
由于计算量太大,直接嘎了。
所以寻求GPU的帮助是必要的,下面看一下论文以及代码再做说明!
前面只是做了一点小的尝试,说明不了任何问题,只是在使用它的过程中需要考虑维度的计算问题。
还是从理论来阐述一下KAN的作用吧。
论文链接:
https://arxiv.org/pdf/2404.19756
现在已经是v4.0版本了。
摘要:
受到 Kolmogorov-Arnold 表征理论的启发,K-A Network或者叫KAN就在这篇文章中被提出来,它其实是多层感知机的一个变体,或者说是可替代物。二者的主要区别在于激活函数,MLP是固定的,而KAN是可学习的。
KAN最大的特点就是毫无线性化的参数,都是非线性映射。所以它的学习表征能力被极大的提升,并且可解释性也大大提高。
其实这一点(而KAN的激活函数是可学习的),在整个网络演变中,研究人员都倾向于用可变学习的方式提高网络的自适应性。
前面的版本中只是说能够使用CPU进行KAN网络的训练,这对于现有的大量使用GPU的训练是很不友好的。
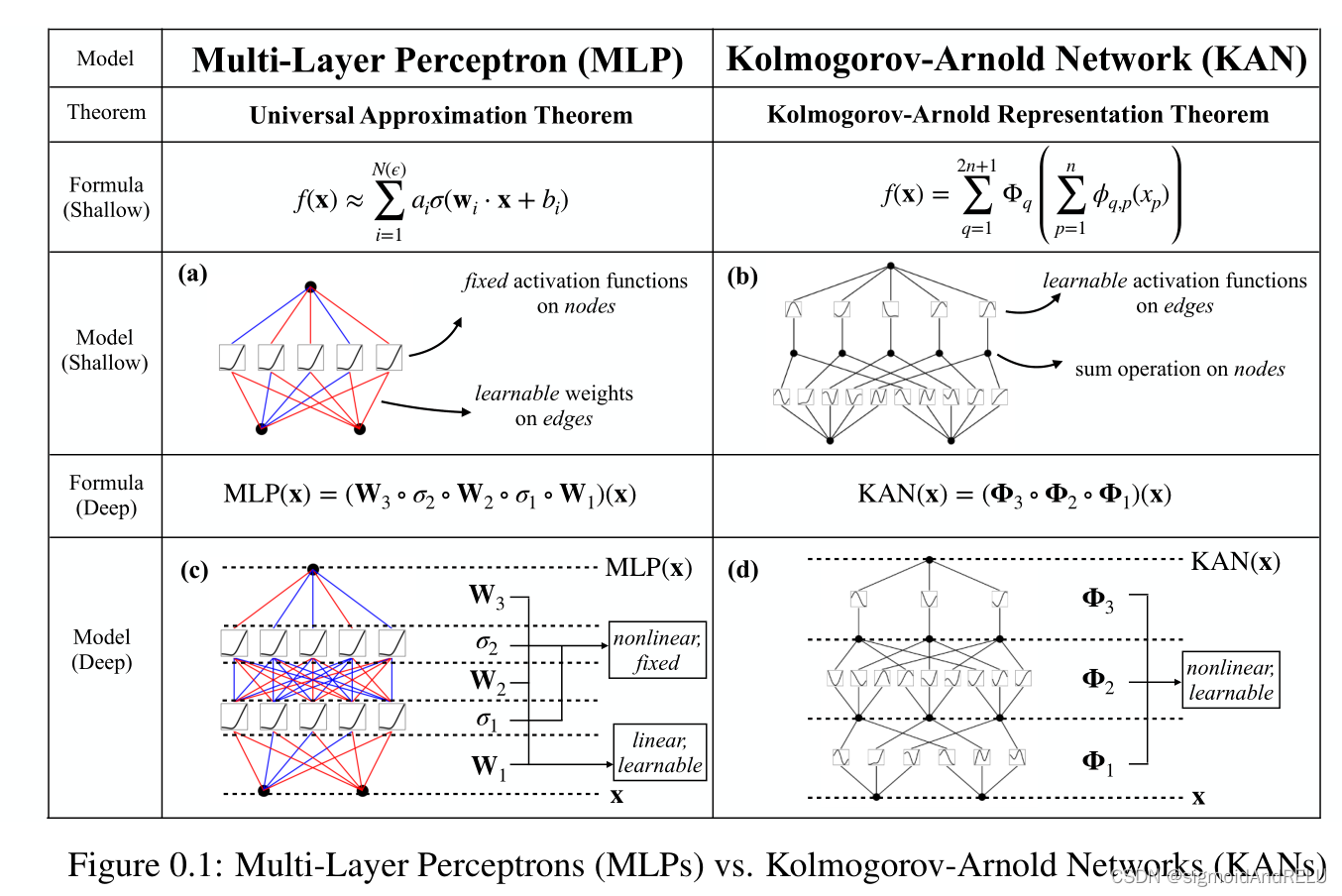
这张图很形象的告诉我们,多层感知机和KAN的区别,主要是激活函数的位置和可训练方式,然后特征的转换公式也有很大区别。
看公式:
MLP:
M
L
P
(
x
)
=
(
W
3
∘
σ
2
∘
W
2
∘
σ
1
∘
W
1
)
(
x
)
MLP(x)=(W_3 \circ \sigma_2 \circ W_2 \circ \sigma_1 \circ W_1 )(x)
MLP(x)=(W3∘σ2∘W2∘σ1∘W1)(x)
f
(
x
)
=
∑
i
=
1
N
(
c
)
a
i
σ
(
W
i
x
+
b
i
)
f(x)=\sum^{N(c)}_{i=1}{a_i}\sigma(W_ix+b_i)
f(x)=∑i=1N(c)aiσ(Wix+bi)
KAN:
K
A
N
(
x
)
=
(
Φ
3
∘
Φ
2
∘
Φ
1
)
(
x
)
KAN(x) = (\Phi_{3} \circ \Phi_{2} \circ \Phi_{1})(x)
KAN(x)=(Φ3∘Φ2∘Φ1)(x)
f
(
x
)
=
∑
q
=
1
2
n
+
1
Φ
q
(
∑
p
=
1
n
ϕ
q
,
p
(
x
p
)
)
f(x) = \sum^{2n+1}_{q=1}{\Phi_q(\sum^{n}_{p=1}{\phi_{q,p}(x_p)})}
f(x)=∑q=12n+1Φq(∑p=1nϕq,p(xp))
结合刚刚看的嵌入 embedding的原理,空间向量关系的映射。KAN的非线性映射可学习仿佛包含了复杂的子网embedding技术。
虽然数学公式很简单,但是涉及到非常大的参数学习和训练,一般用的是VIT-32
映射到512的空间中。
一旦这种需要训练的 映射关系多了,那么所需要的计算代价是难以想象的。
回到原文:
尽管KANs的数学表达式是优雅且简洁的,但究其根本,就是spines同MLP的结合,权衡二者的长处。
那么什么是Splines:
样条函数指一种由多项式分段定义的特殊函数,具有独特的数学特性和广泛的应用价值。
通俗讲,样条就是分段函数,每一段都是一个多项式,这不可能用一个多项式来表示。
Splines的特点:样条线对于低维函数是精确的,易于局部调整,并能够在不同的分辨率之间切换。然而,样条曲线存在维数诅咒(Curse Of Dimensionality)问题,因为它们不能利用组合结构。
(所以,它很厉害,它的计算量也很大)
MLP的特点:多层感知机是基于特征学习的,对COD的影响较小,但由于无法优化单变量函数,它们不如低维样条曲线精确。
文中用的例子:
f
(
x
1
,
x
2
,
…
…
,
x
N
)
=
e
x
p
(
1
N
∑
i
=
1
N
s
i
n
2
(
x
i
)
)
f(x_1, x_2, ……, x_N) = exp(\frac{1}{N}\sum^{N}_{i=1}{sin^{2}(x_i)})
f(x1,x2,……,xN)=exp(N1∑i=1Nsin2(xi))
当 N太大,样条函数就因为维度约束,拟合失败,而MLP可以潜在地学习广义的加性结构,但它们对于近似指数函数和正弦函数非常低效。所以在这个公式计算上都不行。
KANs 将这两者结合起来,获得了不错的效果。
作者甚至直接将KAN作为一个库发布到了python中,pip install pykan
这里面的内容当然是可以修改的,我们先看内容。
Kolmogorov-Arnold Representation theorem
这个 KA表征理论是核心,也是KAN网络的根本。
这两个人 Vladimir Arnold Andrey Kolmogorov 建立了一个理论:
如果 f 是一个有界的多变量连续函数,那么它就可以被单变量的连续函数的组合所替代(改写成)。也就是一个多变量函数可以写作单变量的多项式累加。
准确的来说:
对于一个 平滑函数
f
:
[
0
,
1
]
n
→
R
f:[0, 1]^ n \rightarrow R
f:[0,1]n→R
f ( X ) = f ( x 1 , x 2 , … , x n ) = ∑ q = 1 2 n + 1 Φ q ( ∑ p = 1 n ϕ q , p ( x p ) ) f(X) = f(x_1, x_2,…, x_n) = \sum^{2n+1}_{q=1}{\Phi_q(\sum^{n}_{p=1}{\phi_{q,p}(x_p)})} f(X)=f(x1,x2,…,xn)=∑q=12n+1Φq(∑p=1nϕq,p(xp))
其中,
ϕ
q
,
p
:
[
0
,
1
]
→
R
\phi_{q,p}:[0, 1] \rightarrow R
ϕq,p:[0,1]→R , 而
Φ
q
:
R
→
R
\Phi_{q}: R \rightarrow R
Φq:R→R
在某种意义上,他们表明了唯一真正的多元函数是加法。
所以,理论上,所有的多变量都可以变成单变量的多项式求和。这对于机器学习而言是较困难的,理论上完全可以实现,但操作起来不可能。
本文在理论的基础上思考如何实现:
首先,我们不需要坚持使用原来的等式(2.1)它只有两层非线性和少量的项(2n+1):我们将把网络推广到任意宽度和深度。
其次,科学和日常生活中的大多数功能通常是平滑的,并具有稀疏的组成结构,有可能促进平滑的KA representation。
这里的哲学是接近于物理学家的心态,他们通常更关心典型的情况,而不是最坏的情况。
毕竟,我们的物理世界和机器学习任务必须有使物理和机器学习有用或完全一般化的结构。
上述是思想和理论部分,我依稀记得,当初有理论说,两层无限参数量的多层感知机能够实现一切要求的映射,而这应该是理论的来源,当初没有细究。
KAN 架构
跟着论文中的公式讲诉,我们来过一遍:
假定我们有一个监督学习任务,输入输出为
{
x
i
,
y
i
}
\{x_i, y_i\}
{xi,yi}, 这里,我们试图找到一个让
y
i
=
f
(
x
i
)
y_i = f(x_i)
yi=f(xi)的函数。而等式中表明,我们如果能够找到合适的单变量函数
ϕ
q
,
p
\phi_{q,p}
ϕq,p和
Φ
q
\Phi_q
Φq,就能够满足这一点。
这启发了我们,如果能够设计一个神经网络来找到这些参数就可以。
由于所有的方法都是单变量的,就可以将每一个函数都作为B-样条曲线。
也就是贝塞尔曲线。
现在,我们有了KAN的prototype,计算图也可以画出来。
还是跟着公式走一遍:
注意,这个网络
我先看到了KAN的符号回归可视化,确实很震惊:
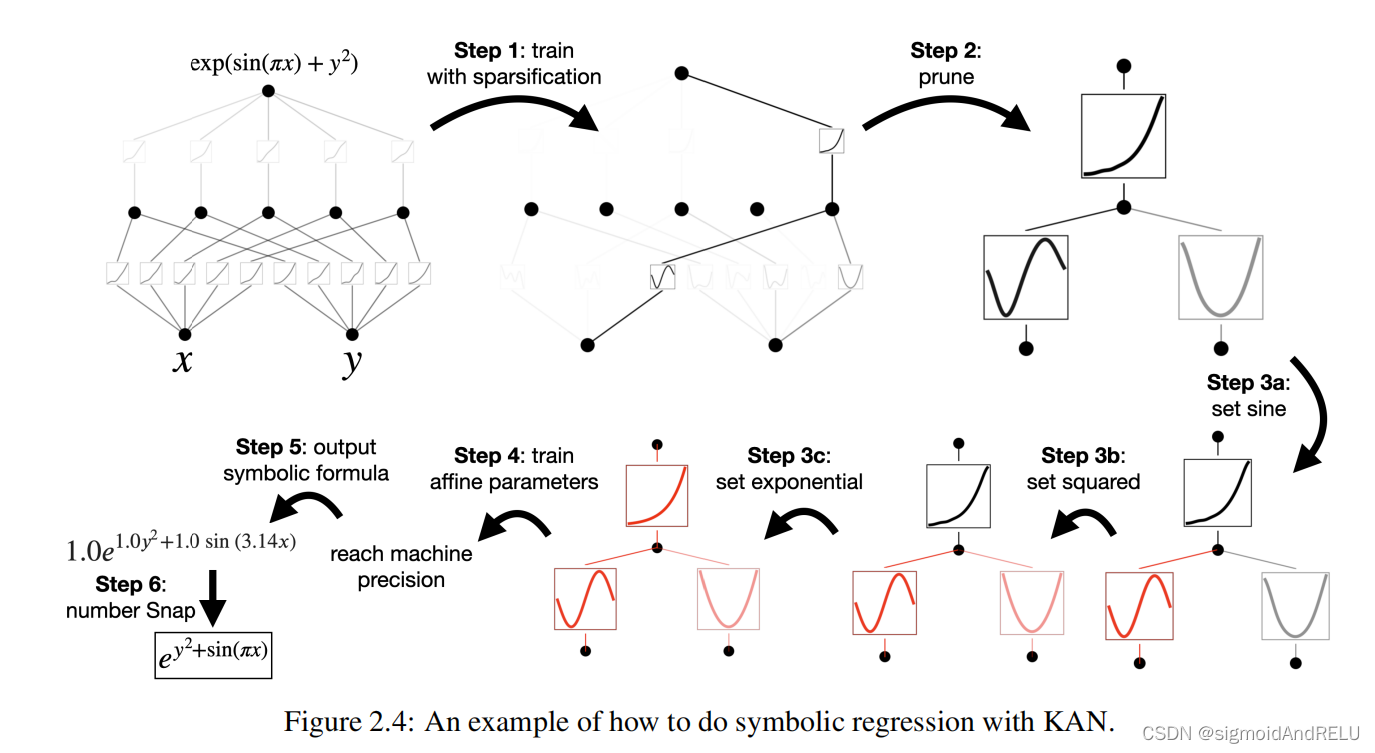





















 1143
1143











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








