【机器学习】——PCA算法的实现

Melodycy456

已于 2024-06-18 17:16:02 修改

阅读量771

点赞数 26

文章标签：信息可视化人工智能

于 2024-06-18 17:10:50 首次发布

本文链接：https://blog.csdn.net/qq_73559660/article/details/139777911

版权

PCA（Principal Component Analysis，主成分分析）算法是一种广泛使用的线性降维算法，尤其在机器学习和数据分析领域。以下是关于PCA算法的详细介绍：

一、算法概述

1.1 算法简介

PCA是一种数据维度压缩和特征选择的方法，它通过将高维数据映射到低维数据，保留数据的主要特征，从而实现数据的降维。PCA算法的核心思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征，也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

1.2 算法原理

PCA算法的原理主要包括以下几个方面：

特征提取：对于给定的数据集，PCA首先需要找到其中最重要的特征，即主成分。这些主成分是与原始数据最为相关的特征向量，或者说是最能代表原始数据特征的线性组合。

降维处理：在得到数据集的主成分之后，PCA使用这些主成分将原始数据降维到一个低维度的空间。在这个低维度空间中，数据点之间的距离和分布与原始数据点之间的距离和分布相似。

矩阵运算：PCA算法的核心是矩阵运算。一般来说，PCA算法的实现需要计算数据集的协方差矩阵，通过对协方差矩阵进行SVD分解（奇异值分解），得到主成分和对应的特征向量。

可视化：通过PCA算法得到的降维数据可以进行可视化，便于数据分析和展示。

1.3 算法步骤

PCA算法的主要步骤包括：

数据预处理：对数据进行标准化处理，消除量纲的影响。

计算协方差矩阵：计算数据的协方差矩阵，表示数据各个维度之间的相关性。

计算公式为： $(C = \frac{1}{n-1} \sum_{i=1}{n} (x_i - \bar{x})(x_i - \bar{x})T)$
其中，(C)为协方差矩阵，(n)为样本数量，( $x_i$ )为第(i)个样本，( $\bar{x}$ )为样本均值。

计算特征值和特征向量：对协方差矩阵进行特征分解，得到特征值和特征向量。

选择主成分：按照特征值的大小选择前k个特征值对应的特征向量，这k个特征向量就是主成分。

数据降维：将原始数据投影到由主成分构成的低维空间中，得到降维后的数据。

1.4 应用场景

PCA算法的应用场景非常广泛，包括但不限于以下几个方面：

人脸识别：当数据量较大时，PCA是非常有效的一种降维方法，能够节约存储空间并提高计算速度。

数据可视化：通过PCA算法得到的降维数据可以进行可视化，有助于数据分析和展示。

特征提取：PCA能够提取出数据中的主要特征，有助于后续的数据分析和挖掘。

1.5 优缺点

PCA算法的优点包括：

无监督学习：PCA不需要标签数据，是一种无监督学习方法。

降维效果好：PCA能够有效地降低数据的维度，同时保留数据的主要特征。

可解释性强：PCA将数据投影到低维空间后，得到的特征向量通常具有直观的含义。

PCA算法的缺点包括：

线性假设：PCA假设数据之间存在线性关系，如果数据之间存在非线性关系，PCA可能无法完全揭示数据的内在结构。

对初始变量敏感：PCA对初始变量的顺序和标签敏感，不同的变量顺序可能导致不同的主成分结果。

无法处理多模态数据：PCA主要处理连续型数据，对于离散型或分类数据表现较差。

二、算法实现

2.1 准备数据

导入鸢尾花数据集

from sklearn import datasets  
import matplotlib.pyplot as plt  
import numpy as np  
from sklearn.decomposition import PCA  
from pylab import mpl  
  
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体  
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题  
  
# 鸢尾花的数据集  
iris = datasets.load_iris()

2.2 PCA降维

这段代码使用了scikit-learn库中的PCA（主成分分析）类，对鸢尾花（Iris）数据集进行了降维处理。首先，它加载了数据集中的特征（X）和标签（y），但没有直接使用标签信息，因为PCA是一种无监督学习方法。接着，代码打印了原始数据集中前三个样本的特征值，以展示数据的原始形态。然后，它创建了一个PCA对象，指定要保留的主成分数量为2，并使用fit_transform方法将原始数据投影到这两个主成分上，实现了数据的降维。之后，代码打印了降维后数据集中前三个样本的主成分值，展示了降维后的数据形态。此外，代码还打印了每个主成分的方差百分比，这些百分比表示了各个主成分在解释数据集中方差时的贡献程度。最后，它打印了所有主成分的方向（即主成分向量），这些向量显示了数据集中各个特征在每个主成分上的权重，反映了特征对主成分的贡献程度。整个流程展示了如何使用PCA对高维数据进行降维处理，并分析了降维后的数据特性。

X = iris['data']  
y = iris['target']  
target_names = iris['target_names']  # 获取类别标签名  
  
print('Before pca: \n', X[:3,:])  
  
pca_1 = PCA(n_components=2)  
X_red_1 = pca_1.fit_transform(X)  
  
print('After pca: \n', X_red_1[:3, :], '\n')  
print('方差百分比: ', pca_1.explained_variance_ratio_)  
print('总方差百分比: ', pca_1.explained_variance_ratio_.sum(), '\n')  
print('components_: \n', pca_1.components_)  解释这段代码

2.3 结果可视化

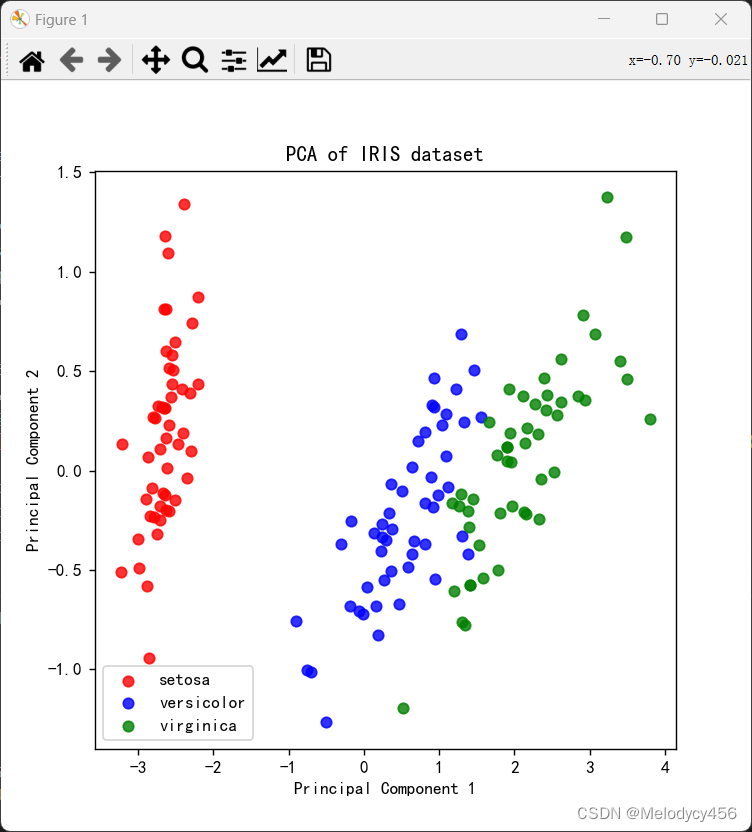
# 结果可视化  
plt.figure(figsize=(6, 6))  
colors = ['red', 'blue', 'green']  # 为每个类别指定颜色  
for i, color in zip(range(3), colors):  
    plt.scatter(X_red_1[y == i, 0], X_red_1[y == i, 1], alpha=0.8, label=target_names[i], color=color)  
plt.legend()  
plt.title('PCA of IRIS dataset')  
plt.xlabel('Principal Component 1')  
plt.ylabel('Principal Component 2')  
plt.show()

2.4 整体代码

from sklearn import datasets  
import matplotlib.pyplot as plt  
import numpy as np  
from sklearn.decomposition import PCA  
from pylab import mpl  
  
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体  
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题  
  
# 鸢尾花的数据集  
iris = datasets.load_iris()  
X = iris['data']  
y = iris['target']  
target_names = iris['target_names']  # 获取类别标签名  
  
print('Before pca: \n', X[:3,:])  
  
pca_1 = PCA(n_components=2)  
X_red_1 = pca_1.fit_transform(X)  
  
print('After pca: \n', X_red_1[:3, :], '\n')  
print('方差百分比: ', pca_1.explained_variance_ratio_)  
print('总方差百分比: ', pca_1.explained_variance_ratio_.sum(), '\n')  
print('components_: \n', pca_1.components_)  
  
# 结果可视化  
plt.figure(figsize=(6, 6))  
colors = ['red', 'blue', 'green']  # 为每个类别指定颜色  
for i, color in zip(range(3), colors):  
    plt.scatter(X_red_1[y == i, 0], X_red_1[y == i, 1], alpha=0.8, label=target_names[i], color=color)  
plt.legend()  
plt.title('PCA of IRIS dataset')  
plt.xlabel('Principal Component 1')  
plt.ylabel('Principal Component 2')  
plt.show()