Thomas-Calculus——Infinite Sequences and Series-The integral test(托马斯-微积分——无穷数列和级数-积分测试)

不爱敲代码的数学分子

于 2023-06-25 14:11:21 发布

阅读量651

点赞数 2

文章标签：几何学抽象代数

本文链接：https://blog.csdn.net/qq_73627657/article/details/130875953

版权

介绍

关于级数，我们最关心的就是它是否收敛，在之前的文章中已经介绍了一种判断级数敛散性的方法——通过判断部分和(partial sum)的敛散性来得出级数是否收敛，如果我们不能写出部分和的通项公式，则通过nth-term test判断级数的敛散性。

调和级数(harmonic series)

调和级数(harmonic series)是P级数(P-series)的一种，形如下图：

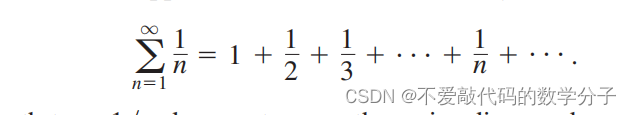
调和级数中 $a_{n}$ = $\frac{1}{n}$ ，根据nth-term test是无法判断调和级数的敛散性的。

根据定理6的推论，调和级数是发散的。

积分测试

这个类似于调和级数的级数收敛吗？

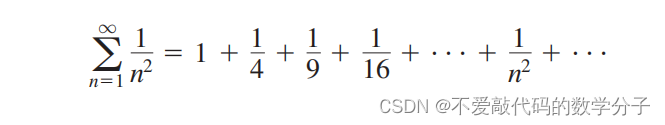
我们通过与 $\int_{1}^{\propto }\left ( \frac{1}{x^{2}} \right )dx$ 比较来确定上面级数的敛散性，为了进行比较，我们将上面级数的项看作函数 $f(x) = \frac{1}{x^{2}}$ 的值，然后把函数值作为矩形的右顶点，底部x轴宽度看作是1，所以矩形的面积还是函数值，也是级数各项的值。

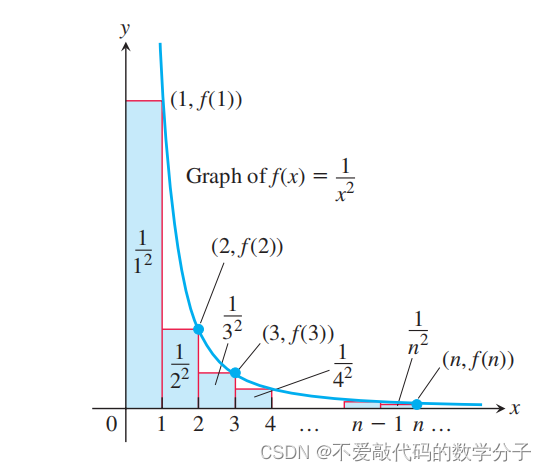
因此， $\sum_{n = 1}^{\propto }(\frac{1}{n^{2}})$ 的部分和被2限制，所以，该级数是收敛的。

积分测试的定义

定义的翻译比较拗口，简单地讲，积分测试的定义有这样几个前提条件(premise)：1、数列{ $a_{n}$ }各项都是正数。2、 $a_{n}$ = f(n)。3、函数f(x)对于所有x $\geq$ N(N是一个正数)连续、大于零并且递减。满足这些条件，则级数 $\sum_{n = N}^{\propto }$ $a_{n}$ 和积分 $\int_{N}^{\propto }$ f(x) dx 都是收敛或发散。

证明：假设条件中的N = 1(对一般的N的证明也是相似的)，函数f(x)是递减的并且对所有的n， $a_{n}$ = f(n)，使函数值等于数列值构成的矩阵的左上顶点对应的值：( n, f(n) )。

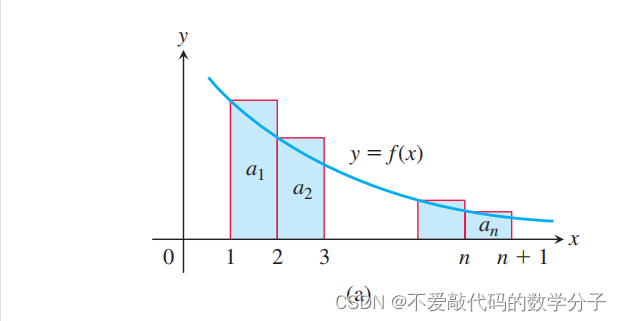
由图(a)可知，使函数值等于数列值构成的矩阵的右上顶点对应的值， $a_{n}$ 的前n项部分和(矩形面积的和)大于 $\int_{1}^{n+1}$ f(x) dx，所以 $a_{1}$ + $a_{2}$ + $a_{3}$ + $a_{4}$ + $a_{5}$ +···+ $a_{n}$ >= $\int_{1}^{n+1}$ f(x) dx。

由图(b)可知， $a_{n}$ 的前n项部分和(矩形面积的和)小于 $\int_{1}^{n}$ f(x) dx，所以 $a_{1}$ + $a_{2}$ + $a_{3}$ + $a_{4}$ + $a_{5}$ +···+ $a_{n}$ <= $\int_{1}^{n}$ f(x) dx。

所以，结合上面两张图得出的不等式可知， $\int_{1}^{n+1}$ f(x) dx <= $a_{1}$ + $a_{2}$ + $a_{3}$ + $a_{4}$ + $a_{5}$ +···+ $a_{n}$ <= $\int_{1}^{n}$ f(x) dx。当n $\rightarrow$ $\propto$ 时， $\int_{1}^{n+1}$ f(x) dx和 $\int_{1}^{n}$ f(x) dx都会变成 $\int_{1}^{\propto }$ f(x) dx，所以，如果 $\int_{1}^{\propto }$ f(x) dx是有界的，那么 $\sum a{_{n}}^{}$ 也是有界的，反之亦然。

所以，积分测试可以作为一种判断级数敛散性的方法，但是对级数和对应的函数都有要求。积分测试还需要用到反常积分的知识。需要注意的是，通过积分测试得出的结果只是用来判断级数的敛散性，不能直接等于级数的结果。

P-级数

P-级数形如 $\sum_{n=1}^{\propto }\frac{1}{n^{p}}$ ，其中p是实数。当p>1时， $\sum_{n=1}^{\propto }\frac{1}{n^{p}}$ 收敛，当p<1时， $\sum_{n=1}^{\propto }\frac{1}{n^{p}}$ 发散。

证明(运用积分测试)：

在P-级数中，当P=1时，就是调和级数，所以调和级数是P-级数的一种特殊情况。

误差估计

在上面提到的积分测试中，无论是使函数值等于数列值构成的矩阵的左上顶点对应的值，还是使函数值等于数列值构成的矩阵的右上顶点对应的值，都不能完全等于级数的值，这就会造成误差。

假设 $\sum$ $a_{n}$ 各项为正数并且根据积分测试级数是收敛的。令差数 $R_{n}$ = S- $s_{n}$ ，其中S是级数的值， $s_{n}$ 是级数的部分和的值，所以 $R_{n}$ = $a_{n+1}$ + $a_{n+2}$ + $a_{n+3}$ + $a_{n+4}$ + $a_{n+5}$ ···。

根据图(a)，函数值等于数列值构成的矩阵的左上顶点对应的值，所以 $R_{n}$ >= $\int_{n+1}^{\propto }$ f(x) dx

根据图(b)，函数值等于数列值构成的矩阵的左上顶点对应的值，所以 $R_{n}$ <= $\int_{n}^{\propto }$ f(x) dx

所以，根据上面的两个不等式，可以得出 $\int_{n+1}^{\propto }$ f(x) dx<= $R_{n}$ <= $\int_{n}^{\propto }$ f(x) dx。

因为 $R_{n}$ = S- $s_{n}$ ，所以， $s_{n}$ + $\int_{n+1}^{\propto }$ f(x) dx<=S<= $s_{n}$ + $\int_{n}^{\propto }$ f(x) dx。

在对级数应用积分测试求其敛散性的时候，可以通过上述不等式组求出级数的大致范围。

不爱敲代码的数学分子

关注

2
点赞
踩
2

收藏

觉得还不错? 一键收藏
打赏
1
评论
Thomas-Calculus——Infinite Sequences and Series-The integral test(托马斯-微积分——无穷数列和级数-积分测试)

关于级数，我们最关心的就是它是否收敛，在之前的文章中已经介绍了一种判断级数敛散性的方法——通过判断部分和(partial sum)的敛散性来得出级数是否收敛，如果我们不能写出部分和的通项公式，则通过n判断级数的敛散性。1、数列{}各项都是正数。2、= f(n)。3、函数f(x)对于所有xN(N是一个正数)连续、大于零并且递减。满足这些条件，则级数和积分f(x) dx 都是收敛或发散。证明：假设条件中的N = 1(对一般的N的证明也是相似的)，函数f(x)是递减的并且对所有的n，
复制链接

扫一扫